高考中物理學科有關極值問題的處理方法之分析
朱震文
(湖南省永州市祁陽縣第二中學)
物理學科極值問題在歷年高考理科綜合中經常出現,怎樣處理極值問題,大部分考生感覺比較棘手,結合多年高三的教學經驗,及學生在處理這類問題中存在的疑問,談一談這類問題的處理方法。
首先,對極值問題的處理,必須培養學生具有較高的綜合問題的處理能力,即既要有比較嫻熟運用物理規律處理物理問題的能力,又要有比較高的運用數學方法處理物理問題的能力。在具有這些基本能力的基礎上,還應培養學生對極值問題有一個系統的歸類分析,大致講物理學科的極值問題在處理過程中的方法可以分成兩大類:物理方法和數學方法。
物理方法就是從物理學的角度,應用物理定義、物理規律對極值問題進行分析判斷,找出問題過程中出現極值的時間點或位置點,再應用相應的物理規律列出物理等式加以求解。
物理分析方法有三角形矢量分析法、臨界條件分析法等。
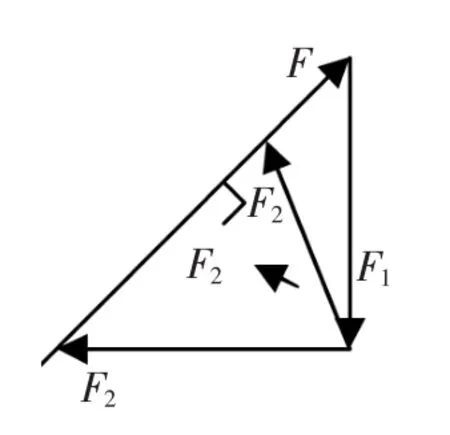
方法一:三角形矢量分析法就是應用力的矢量三角形的邊角的關系,已知合力的方向和另一分力的大小和方向時,點到直線的垂直距離最小,如圖所示:兩個分力F1、F2和合力F構建一個矢量三角形,在已知合力F的方向和另一分力F1的大小和方向時,只有F2與合力F垂直時有最小值。場力方向與v0方向垂直時有最小值,如右圖所示。
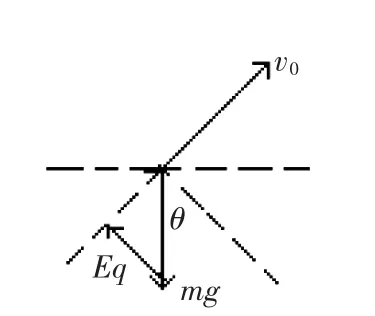
解答:如圖所示,要保證微粒沿v0方向直線運動必須使垂直于v0向斜上方加勻強電場E有最小值,且Eq=mg cosθ,E=mg cosθ/q。
方法二:臨界條件分析法就是通過對研究對象的分析,找出物體在研究過程中可能出現的臨界條件,再應用相關的物理規律加以求解。
例題2:如圖所示,光滑水平面上放置質量分別為m和2m的四個木塊,其中兩個質量為m的木塊間用一不可伸長的輕繩相連,木塊間的最大靜摩擦力是μmg。現用水平拉力F拉其中一個質量為2 m的木塊,使四個木塊以同一加速度運動,則輕繩對m的最大拉力為_______.
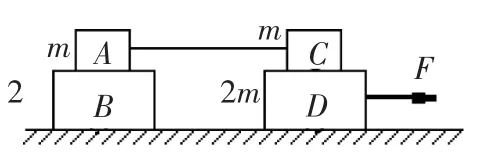
試題分析:本題的關鍵是要想使四個木塊一起加速,則任兩個木塊間的靜摩擦力都不能超過最大靜摩擦力。首先要找出A和B、C和D這兩對物體之間,哪一對物體間首先到達最大靜摩擦力這一臨界條件。由題意可知A和B的靜摩擦力僅是B物體產生加速度的動力,而C和D間的靜摩擦力是A、B、C三個物體產生加速度的動力,所以C和D這兩對物體之間先到達最大靜摩擦力這一臨界條件。
解答:對 A、B、C 三個物體作為整體有:fm=4ma,T=3ma,又有:fm=μmg以上各式聯立解得T=.
數學方法就是應用物理規律對物理極值問題進行分析之后,確定研究對象及研究過程,列出相關的數學表達式,再應用不同的數學工具加以處理。根據應用不同的數學方法,大致可以從四個方面加以處理。
第一種方法稱之為二次函數法:二次函數法就是關于y=ax2+bx+c的應用,根據二次函數的特點,a>0時,圖像開口向上,y有最小值;a<0時,圖像開口向下,y有最大值。且只有x=-時,y有最值。
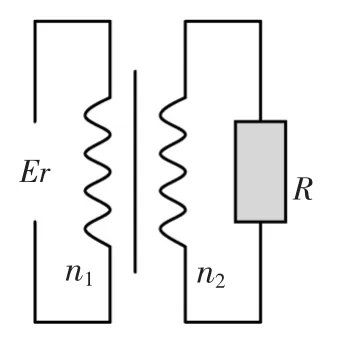
例題3:如圖所示,理想變壓器輸入端接在電動勢為ε,內阻為r的交流電壓上,輸出端接負載R,則變壓器原副線圈的匝數比為多大時,負載R上消耗的電功率最大?
解答:設原副線圈的匝數分別為n1,n2,電流分別為 I1,I2,電壓分別為 U1,U2,
則:U1=ε-I1r電阻R消耗的電功率為P=U2I2=U1I1
即 P=(ε-I1r)I1=-I21·r+εI1
可見當:I1=時,P有最大值Pmax=
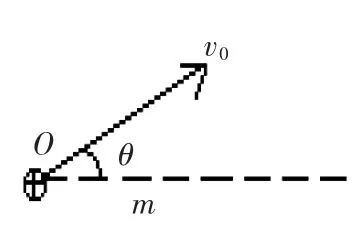
例題1:如圖所示,質量為m,帶電量為+q的微粒在O點以初速度v0與水平方向成θ角射出,微粒在運動中受阻力大小恒定為f。如果在某方向加上一定大小的勻強電場后,能保證微粒仍沿v0方向做直線運動,試求所加勻強電場的最小值?
試題分析:本題的根本在于確定電場力沿什么方向有最小值,由題意分析可得,只有當電場力與重力的合力與初速度方向在一條直線上,才能達到題中的要求,又由矢量三角形原理可得當電
第二種方法稱之為三角函數法:通過設定角度為一函數變量,應用物理規律列出相關的方程,然后加以處理。
例題4:半徑為R的絕緣光滑圓環固定在豎直平面內,環上套有一質量為m,帶正電的珠子,空間存在水平向右的勻強電場。如圖所示,珠子所受電場力是其重力的倍。將珠子從環上最低位置A點靜止釋放,則珠子所能獲得的最大動能為多少?
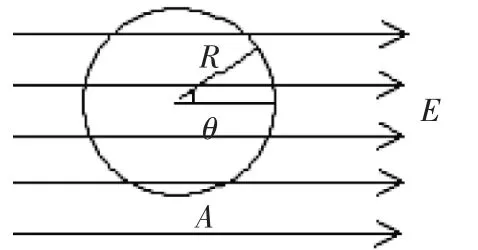
解答:設珠子的帶電量為q,電場強度為E。珠子在它與電場線的夾角為θ時,珠子所能獲得的動能最大,如圖所示,則由動能定理得珠子動能的表達式為 Ek=qER cosθ-mgR(1-sinθ),
利用三角變換可得:Ek=qER cosθ-mgR(1-sinθ)=3 mgR cosθ4 mgR sinθ-mgR.
第三種方法稱之為不等式法:不等式法就是如果兩數和為常數,當兩數相等時其乘積最大,由若 x+
y=P(定值),則當 x=y時,x、y的乘積有極大值。
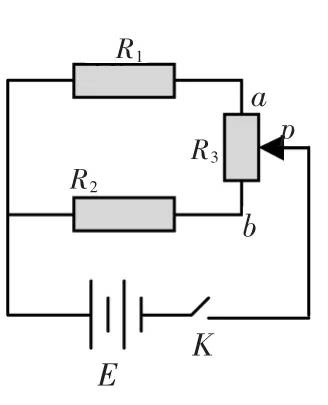
例題5:如圖所示,已知R1=2Ω,R2=3Ω,R3=5Ω,電源電動勢 ε=6V,電源內阻r=0.5Ω。問:變阻器滑動片在何處時,電源發熱功率最小?
解答:設電源發熱功率為P,干路電流為 I,據 P=I2·r,可知:I最小時,P 最小。
根據不等式原理可知:當R1+Rx=R2+R3-Rx時,I有最小值。
第四種方法稱之為導數法:導數法就是應用數學中求導與極值的關系,對物理方程加以處理而求解。
例題6:一輕繩一端固定在O點,另一端拴著一小球,拉起小球使輕繩水平,然后無初速地釋放,如圖所示,小球在運動至輕繩達到垂直位置過程中,小球所受重力的瞬時功率在何處取得最大值。

解答:設繩達到與水平方向為角a時,重力的功率取得最大值,則速度v和重力mg之間的夾角也為a,對小球從A到C由動能定理,則有:mgR sin a=mv2,其中 R 為輕繩長。
以上求極值的方法是解高中物理題的常用方法。在求解極值問題的過程中,首先應對這類問題加以歸類分析,確定問題應該使用物理方法還是數學方法的總的解題方向,然后根據題意,找出符合物理規律的物理方程或物理圖象,最終得以求解。

