“知行合一”教學模式在線性代數教學中的應用
劉倩 孫丹娜 許洋

摘 要 “知行合一”是王陽明早期的哲學思想,也是習近平主席推薦六次的哲學理念,“知行合一”的教學模式探討是當前教學研究的一個重要話題,本文就是從其內涵和線性代數的學科特征著手,剖析當前學校課堂教學中存在的問題,研究了在大類招生的背景下,“知行合一”教學模式在線性代數教學中的應用,最終體現了線性代數集理論、實踐、計算機技術于一體的學科特點。
關鍵詞 知行合一 線性代數 教學模式 應用
中圖分類號:G642 文獻標識碼:A 文章編號:1002-7661(2015)21-0004-02
線性代數是求解線性方程組的一個有力工具,幾乎滲透在生活中的各個領域,同時伴隨著計算機技術的飛速發展,這門古老的數學分支其重要性和實用性日益顯著。關于它的教與學的研究也已有時日,但時至今天仍然是一個備受關注的問題。王陽明的“知行合一”理論,闡述了理論與實踐的關系,而線性代數作為一門綜合了數學理論、實際應用、計算機技術的數學基礎課程來說,恰好完美地闡釋了“知行合一”理論。實踐證明,當“知行合一”理論應用到線性代數教學中,極大地激發了學生的學習興趣,形成了良好的師生互動,取得了不錯的教學效果。
一、當前線性代數教學中存在的問題
(一)在大類招生的環境下,學生的主體發生改變。以我校為例,學生的公共基礎課程幾乎都安排在大一,線性代數課程一般安排在大一下半學期,學生的課業繁重,同時線性代數的教學時數少(32學時),教與學的時間相對緊張,如何真正消化理解教學內容是一個大問題。
(二)就教學內容而言,我國傳統的線性代數教材一般偏于理論知識的講授,強調知識體系的邏輯性和完整性,這對于培養學生的數學素質是非常有益的;但由于缺少針對學生專業的應用,學生會因知識的抽象而喪失學習興趣,進而在學業上裹足不前。
(三)就教學效果來看,線性代數是一門系統的學科,但在教學過程中,教師由于學時的原因,課上滔滔不絕生怕完不成教學內容,而學生接受到的主要就是知識碎片,形成不了認識上的連貫性、系統性,只見樹木不見森林,整個線性代數學下來總是糊里糊涂。
(四)就教學關系來看,傳統的教學模式中教師是主體,主要采取講授為主的教學方式,學生被動接受知識,興趣不高,又由于知識本身的抽象性,很容易在聽課過程中分散精力,造成聽課的效率低下。
二、“知行合一”教學模式
王陽明的“知行合一”主張:“知中有行,行中有知”“以知為行,以行為之”。這里的知,我們指科學知識,行指應用實踐。王陽明主張知行是一回事,反對知行脫節甚至知而不行,這在今天,特別是在線性代數的教學過程中,都具有積極意義。線性代數來源于實踐,最終也要回歸于實踐。“知行合一”這一特點恰好完美地在線性代數教學中得到驗證。
(一)教學過程中緊緊圍繞求解線性方程組這個核心
大多數學生更容易接受形象化的概念,通過以解簡單的線性方程組為引例,對于學生來說比較直觀,可以自然地過渡到到行列式和矩陣的章節。比如在講授行列式的時候,由于開篇就導入了線性方程組這個大的背景,所以盡管學生有不同的數學基礎,但都很容易產生強烈的興趣,在好奇心的驅動下,一般一個題目都會主動尋求多種方法求解。
例1
解:(法1:化三角形法)
(法2:降價法)
(法3:改進后的化三角形法)
(法4: 拆列法)
由此可見,當學生真正清楚原理之后,在實踐中會自覺地、靈活地去運用,而通過不同解法的比較,會更好地理解各種方法的優缺點,只是理解上會更系統,應用起來也更加靈活,而只有真正會用,才是真正的“知”。
(二)重點強調幾何特點
線性代數的來源之一是解析幾何,而學生們又剛剛學完了微積分課程,所以在教學時把線性代數知識和微積分的解析幾何部分聯系起來,既可以培養學生把代數和幾何、微積分聯系起來的能力,同時對于理解線性代數中的一些復雜概念有所幫助。比如利用施密特正交化方法由線性無關的向量組得到等價的正交向量組,這個內容學生普遍感覺抽象,教學中引入幾何的例子就比較好理解。
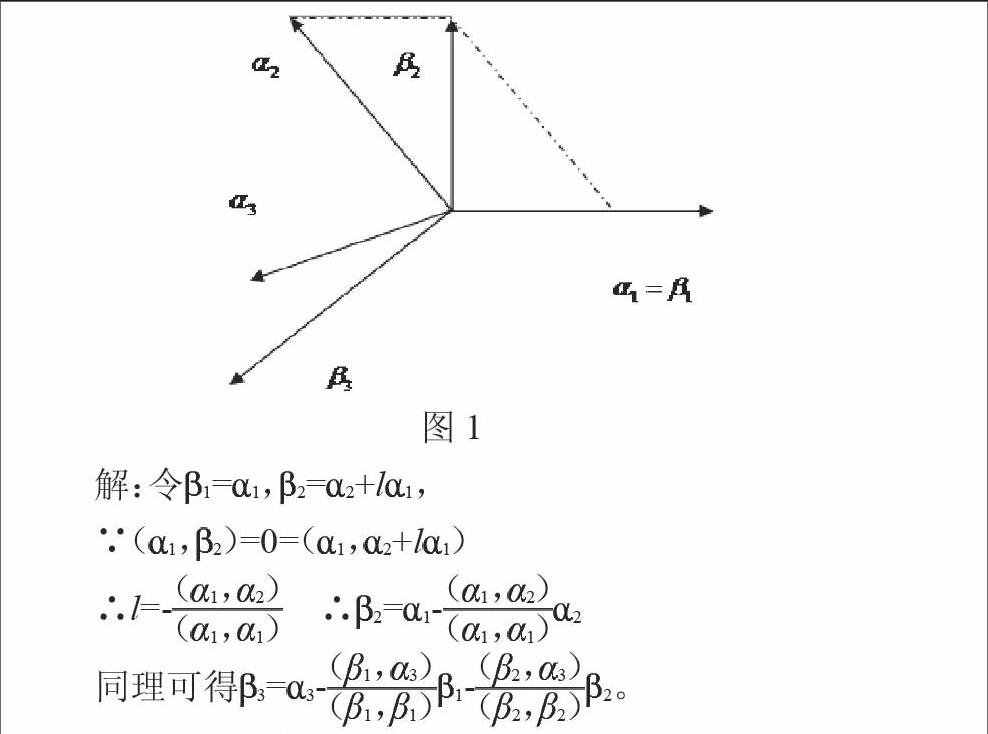
例2 設線性無關的三維向量組 1, 2, 3,利用施密特正交化得到正交向量組。
圖1
解:令 1= 1, 2= 2+l 1,
∵( 1, 2)=0=( 1, 2+l 1)
∴l=- ∴ 2= 1- 2
同理可得 3= 3- 1- 2。
(三)強調實際引用
線性代數當中充斥著大量概念和定理,教師如果照本宣科,學生容易厭煩,理解起來也有一定難度。在實際授課時,盡量和學生的專業相聯系,結合學生的專業特點廣泛取材,利用工程學、生物學、遺傳學、經濟學等學科中的例子解釋基本原理和算法,使學生對所學能有一個直觀的認知,意識到每個知識點都可以轉化為實際應用,從而由被動學習轉變為主動學習。
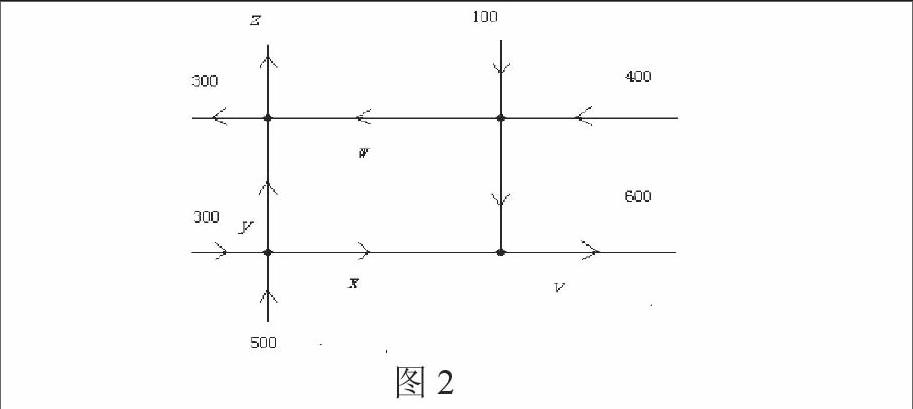
例3 下圖所示是某地區一些單行道路在某時段的交通流量圖:
圖2
寫出該流量的線性方程組
,用相應的矩陣表示為
A=。
顯然可見,各路口的流入流出情況從矩形表中一目了然。通過此例,大家對矩陣概念的導入就易于理解了,并會積極思考如何用矩陣知識求解線性方程組的解(即此網絡中的車流量)。
(四)優化配置習題
1.配置適量的課后習題,便于鞏固、驗證課堂學到的理論知識;要考慮到習題的深度和啟發性,學生不是在機械地模仿教師解題,而是主動思考理解所學的內容。
2.積極參加課程改革實踐,編寫相應的習題指導書。在《線性代數學習指導與習題解答》書中,根據學科特點,總結了各章節的重點、難點、典型方法和題目,為了適應分層教學的需要,在題目設置上,既有適合初學者的基本題目,還有較難的考研題目,對學生理解和應用所學知識很有幫助。
3.結合應用數學軟件Matlab布置習題,體現時代特色。計算機的快速發展直接影響到了線性代數的發展和實踐,利用計算機和線性代數的理論結合起來,可以解決一些實際問題,但考慮到教學時數限制,課上不可能深入討論,我們進行了考核方法上的改進:結合學生的專業特點,布置一定量的拓展作業,既鞏固了基礎知識,又鍛煉了動手能力,深受學生歡迎。
三、小結
線性代數是大學非數學專業的一門非常實用的數學基礎課,地位十分重要,它既有嚴謹的數學理論,還包含豐富的實際應用,再結合應用數學軟件,可以幫助學生掌握后續課程所需要的基本理論和基本技能,對學生來說是最有幫助的一門數學課程之一。當把“知行合一”理論帶入到我們的課堂,線性代數的三個特征完美地體現出來。雖然學時數目有限,很多問題只能淺嘗輒止,但已經把學生的興趣調動起來,整個教學過程都生動活潑,教學也變被動為主動式,學習也不僅僅局限于課堂上。當給學生的心靈插上翅膀時,他們就能賦予未來無限可能。
參考文獻:
[1]汪雷,宋向東.線性代數及其應用[M].北京:高等教育出版社,2001.
[2]鐘志賢.大學教學模式改革的十大走向[J].中國高教研究,2007,(01).
[3]度陰山.知行合一王陽明[M].北京:聯合出版公司,2014.
注:山東省教育科學“十二五”規劃課題(2013GG096)
(責任編輯 曾 卉)

