圓筒框架穩定分析

嚴 峰

(中石化上海工程有限公司，上海 200120)

1 工程簡介

某海外項目4 000 m3料倉鋼支承結構，結構形式為空心圓筒式框架，框架沿徑向沒有任何梁的約束，僅沿圓切線方向布置了封閉柱間支撐，如圖1 所示。常規的鋼結構穩定分析首先需要根據框架兩個主軸方向是否設置了柱間支撐，柱間支撐的剛度是否滿足強支撐要求來區分其屬于有側移失穩還是無側移失穩，進而確定不同的計算長度系數開展后續分析。這類圓筒框架難以簡單區分側移情況，需要綜合計入各種構件相互之間約束影響，按結構穩定理論的方法來進行相關設計。本文從多方法對此類框架的整體穩定性做了細致的研究。

圖1 料倉框架計算簡圖及Load Cell 照片

料倉框架主要由三部分組成，最頂部為鋼結構平臺和相關風送系統管線及其支架，頂平臺主要支承在料倉筒壁上(圖中未顯示)。中間層為料倉本體，底層為高度17 m 的鋼結構圓筒形框架。本結構特殊之處還在于料倉材質為鋁材，設備剛度偏弱且主要通過稱重模塊(Load Cell)支承在柱頂環梁上，稱重模塊與環梁采取了限位裝置防止其大位移滑移除此之外沒有其他強連接。這種連接構造只允許料倉向結構傳遞豎向壓力和水平地震或風荷載，無法形成對下部鋼結構的任何側向剛度約束貢獻。每臺料倉框架共設置8 根框架柱均勻分布在直徑約14 m 的圓周上，框架柱采用焊接雙H 十字形截面，沿結構環向設置連續的柱間支撐，框架徑向由于料倉系統出料的要求不得設置任何構件，整體形成了空心圓筒形式。

2 規范方法

在現行的設計方法中，對于鋼框架結構的穩定分析主要使用的是傳統計算長度法(Effective Length Method)。根據美國國際標準建筑規范ANSI/AISC 360—2005 LRFD［1］(以下簡稱AISC 360)規定若采用計算長度系數法須考慮在每層柱頂施加假想水平力(Additive motional lateral load)來考慮結構整體初始幾何缺陷的影響。AISC 360 規范給出了純彎框架、帶支撐或者剪力墻的框架情況下的計算長度的取值方法，能夠處理多數簡單邊界條件下的桿件計算長度。對于本文這類邊界條件較為復雜的桿件或者非常規的框架，規范給出確定的無側移框架的判別準則為二階位移與一階位移比值:

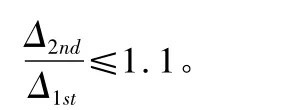
表1 列出了兩種工況下節點一階和二階彈性位移比值，彈性分析時框架位移表現出與常規框架不同的特點。通常情況在豎向和水平荷載作用下框架柱頂位移一般最大，而該料倉框架的各節點側移變形呈現頂層底層大中間層最小，而二階與一階位移比值卻是中間比兩頭大，同類型結構不能僅依據框架柱頂位移比值做簡單判斷。彈性側移分布情況與之字形柱間支撐設置有著密切的關系，框架出現整體繞圓筒切線扭轉的趨勢。驗算結果表明無論正常操作工況還是最大試壓荷載下框架中間節點位移比值處于1.10 限值附近，計算長度系數還需要進一步研究確定。

表1 框架二階與一階彈性位移

3 壓桿屈曲分析

料倉框架結構形式比較規整，可以通過進行合理的假定和簡化構件的邊界條件，根據力學的理論建立微分方程進行求解。計算表明框架柱頂徑向無側移時柱間支撐的最小截面面積要求為23 cm2，通常情況下設置了型鋼截面的柱間支撐都滿足柱頂無側移剛度的要求，因而柱頂可以判定為框架的不動鉸支座，框架可以進一步簡化為多個彈性支承上的軸心受壓構件。

文獻［2］給出了彈性支座壓桿臨界力P 與彈性支座剛度K 的相關性公式如式(1)，其中，P0為中間兩道支撐均為剛性支座時的壓桿臨界力;L 為壓桿長度。式(3)的力學含義為屈曲半波長等于柱間彈性支座的間距，即框架各層均為無側移失穩模態。

取環向典型榀柱間支撐忽略環向撐桿剛度影響，合并整理并考慮柱間環向支撐與框架柱徑向主軸夾角φ=22.5°可以求得二層徑向折算剛度如式(4)。

其中，E 為鋼材彈性模量;Ab和Ac分別為環梁和框架柱截面面積;φ 為柱間支撐夾角;h 為節間高度。

二層徑向剛度:

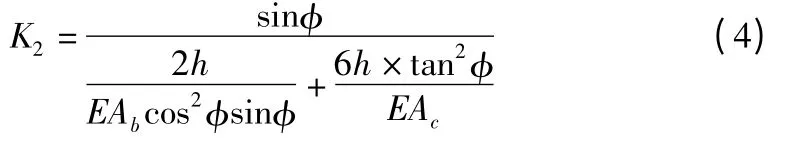
計算長度系數:

根據文獻［3］相關研究，在考慮構件初始屈曲和安裝缺陷要求時，支撐的剛度需要較無缺陷桿件求得的剛度放大2 倍～3 倍。試算表明無論設置多么強大的柱間支撐，其剛度K 均無法滿足式(3)要求，即無法滿足柱中無側移要求。取缺陷折減后的剛度代入聯合求解式(4)和式(5)，可以求得本框架計算長度系數μ 約為0.45。

4 特征值屈曲分析方法

特征值屈曲分析即結構彈性穩定分析(Buckling)，指結構在外荷載作用下，在原來的平衡狀態之外出現結構的分叉點，使用特征值的公式計算造成結構負剛度的應力剛度矩陣的比例因子。特征值屈曲分析的優點是計算快。在進行非線性屈曲分析之前我們可以利用線性屈曲分析了解屈曲形狀，并可以用于確定柱的計算長度系數［4，5］。屈曲分析宏觀上代表了結構失穩的趨勢，與規范規定的方法、物理意義完全不同。由于特征值屈曲不考慮任何非線性和初始缺陷，因此它只是一種理想狀態的解，利用特征值屈曲分析可以預測出屈曲載荷的上限。

采用恒載與活載的荷載組合，求得的前三階屈曲模態如圖2 所示，圖中左側為三維視圖，右側為俯視圖。各階屈曲模態主要表現為平面沒有剛性樓板約束產生沿徑向的變形，該結果與直觀的判斷徑向偏弱基本一致，沒有表現出整層側移屈曲形態。模態2 和模態3 屈曲特征值完全相同僅表現為模態旋轉了90°。

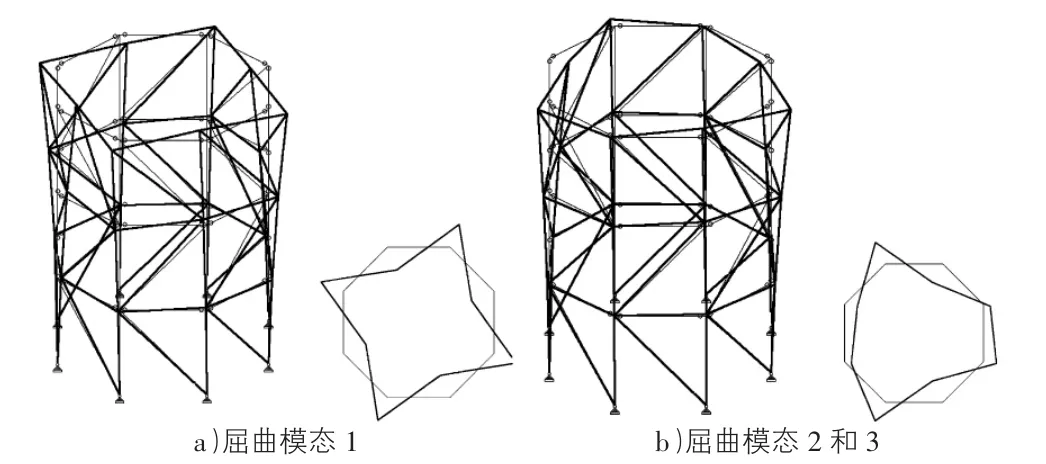
圖2 屈曲模態

表2 列出了前四階屈曲的荷載因子和框架柱計算長度系數情況，通常情況第一階屈曲模態對應的計算長度最為不利，因此該框架柱計算長度為9.8 m。

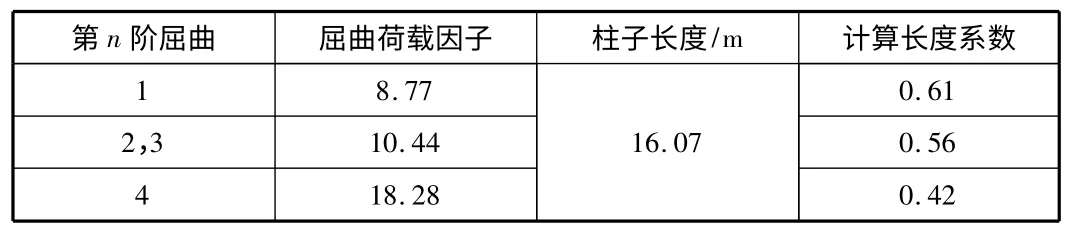
表2 柱計算長度系數

5 精確分析方法

為進一步考查結構的受力性能，對上述框架整體進行了二階非線性彈塑性有限元分析，框架柱截面殘余應力分布情況參考了歐洲鋼結構協會［6］(ECCS)推薦的方案并考慮了焊接十字H 截面腹板部位的焊接應力集中特殊性，見圖3。框架柱頂點側傾缺陷按計，缺陷方位參照特征值屈曲分析模態1。其中，m 為柱列數量。該系數是考慮實際框架中不同柱子的初始缺陷方向可能是不同，產生的不利影響會相互抵消，因此引入作為統計折減系數。另行疊加桿件初始彎曲缺陷，其中，l0為框架柱的層高或者是支撐構件的軸線長度。圖4 為軸力與變形關系曲線，圓點實線為有限元分析結果，兩條虛線分別表示采用折減剛度求得計算長度和屈曲分析得到的計算長度對應的極限承載力。分析結果表明折減剛度得到的極限承載力與有限元分析結果能夠較好吻合，屈曲分析的結果差異稍大。

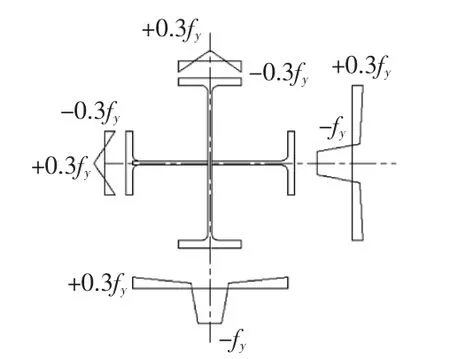
圖3 殘余應力分布

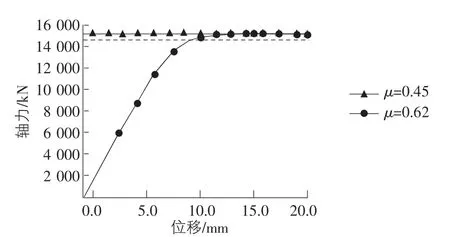
圖4 軸力與變形曲線

6 結語

AISC 360 規范給出根據二階彈性位移和一階彈性分析位移比值小于1.1 時可以按無側移框架求解，該假設要求是有適用條件的。對于本文所示的剪切形圓筒型框架，需要核查每個柱間節點的位移比值，以免造成誤判。

計算表明只要設置很小截面柱間支撐即可滿足框架柱頂無側移的剛度要求，但對于框架中間部位即使設置封閉的柱間支撐依然無法滿足層間無側移剛度要求，因此在設計時應注意驗算柱間支撐的剛度要求。基于折減剛度求得極限承載力與二階彈塑性有限元精確分析吻合程度較高，相關公式滿足工程實用精度需求。

［1］AISC 360，Specification for Structural Steel Building［S］.

［2］陳紹蕃.具有多道彈性支撐桿的鋼柱穩定計算［J］.西安建筑科技大學學報(自然科學版)，2011，43(2):153-159.

［3］童根樹.鋼結構平面內穩定［M］.北京:中國建筑工業出版社，2005.

［4］童根樹，饒芝英.一個奇特的除塵器鋼支架的屈曲問題［J］.建筑鋼結構進展，2007，9(5):42-46.

［5］顧 建.特殊框架柱計算長度的確定［J］.建筑結構，2011，41(sup):926-928.

［6］ENV 1993-1-1，Eurocode 3:Design of Steel Structure Part1.1:General rules for Buildings［S］.