神經網絡預測控制在污水處理溶解氧控制中的應用

張學陽，項雷軍，林文輝，郭新華

（1.華僑大學 信息科學與工程學院，福建 廈門361021；2.泉州市益源環保設備有限公司，福建 泉州362021）

20世紀40年代，國外學者就已開始研究污水處理模型，先后開發出一些簡化的活性污泥法模型.1987年，國際水質協會（IAWQ）在前人研究的基礎上推出了活性污泥1號模型（ASM1），ASM1是活性污泥模型發展的里程碑，成為模擬活性污泥系統的強有力工具［1］.溶解氧（DO）濃度是活性污泥法污水處理曝氣過程中重要的運行控制參數［2－3］，在很大程度上影響著出水水質.因此，研究溶解氧濃度控制有著重要的意義和應用價值.近年來，國內外學者對此做了較為深入的研究，提出了一系列的溶解氧濃度控制方法［4］，如PID 控制［5］、模糊控制［6］、神經網絡控制［7］以及結合前三種方法的優點所提出的綜合方法［8－10］，此外還有模型預測控制［11－12］、遺傳算法［13－14］等.在滿足出水水質要求下，上述方法基本上能對溶解氧濃度進行控制，有效跟蹤溶解氧濃度設定值.但是仍存在一些問題，諸如控制模型受限制前提條件較為苛刻，或僅能實現溶解氧恒定設定值的跟蹤控制，或較少考慮實際過程中外界因素對系統的干擾.綜合神經網絡控制和預測控制兩種方法的優點，基于活性污泥法ASM1標準模型，本文提出一種污水處理溶解氧濃度的神經網絡預測控制器（NNPC）設計方法，在考慮溶解氧測量白噪音干擾和進水流量發生階躍變化情況下，有效實現溶解氧濃度的時變設定值跟蹤控制.

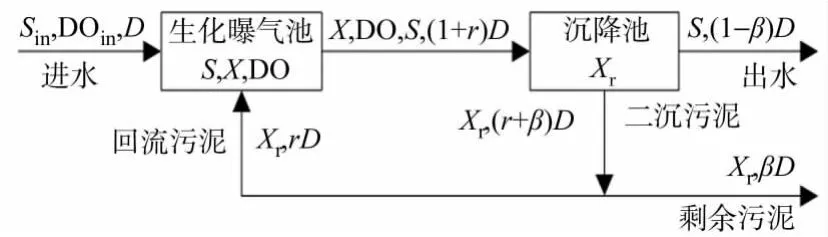
圖1 活性污泥法污水處理工藝流程Fig.1 Schematic representation of the activated sludge sewage treatment process

1 污水處理系統模型的建立

活性污泥法污水處理工藝流程，如圖1所示［1－2］.由圖1可知：系統主要由曝氣池、曝氣系統、沉降池、污泥回流系統和剩余污泥排放系統組成.生化曝氣池是一個混合有液體和固體懸浮物的生物反應器；沉降池是一個利用重力沉降法將污泥從廢水中分離的澄清槽，去除的污泥一部分回流到曝氣池中，剩余一部分污泥被排放出去［2］.

分析活性污泥法污水處理工藝流程，采用ASM1作為控制對象，建立污水處理過程數學模型［3］為

式（1）～（4）中：輸入變量KLa為氧氣傳遞系數，利用KLa描述曝氣過程，KLa和曝氣量W（t）成正比例關系；X（t）為微生物質量濃度；S（t）為底物質量濃度；Xr（t）為回流污泥質量濃度；輸出變量DO（t）為溶解氧質量濃度；β，r為反應速率系數；Y為表現產率系數；Sin，DOin分別為輸入底物濃度和輸入溶解氧濃度；DOs為溶解氧飽和濃度；Kc為常數.

微生物量增長速率為

式（5）中：μmax是最大反應速率；Ks，Ko分別是與底物的質量濃度、溶解氧的質量濃度有關的常數.

式（1）～（5）中各參數的取值規定如下：Y＝0.65；μmax＝0.15h－1；α＝0.018；β＝0.2；r＝0.6；Kc＝0.5；Ko＝2mg·L－1，Ks＝100mg·L－1；Sin＝200mg·L－1；DOin＝0.5mg·L－1；DOs＝10mg·L－1；D（t）＝0.1h－1；W＝80·h－1.變量初始化值如下：X（t）＝200mg·L－1；S（0）＝88mg·L－1；Xr（0）＝88mg·L－1；Xr（0）＝320mg·L－1；DO（0）＝0mg·L－1.

2 溶解氧神經網絡預測控制器的設計

神經網絡具有通過學習逼近任意非線性映射的能力.將神經網絡應用于污水處理過程這類典型非線性系統的建模與辨識，建立污水處理過程的輸入輸出模型，可不受非線性模型類的限制，且便于給出工程上易于實現的學習算法［15］.模型預測控制（MPC）具有3個基本特征：預測模型、滾動優化、反饋校正.MPC是一種典型的約束優化控制方法，在復雜工業過程控制中應用廣泛［16］.但由于模型預測控制方法需要建立被控對象的精確數學模型，且預測模型的精度對模型預測控制器的性能有較大影響，故該方法在非線性系統控制中的應用受到限制.

由于污水處理過程具有嚴重的時滯性、非線性和不確定性.先利用BP神經網絡對系統進行辨識，建立預測控制器的逼近模型；再設計神經網絡預測控制器，通過滾動優化目標值，最終實現溶解氧濃度的時變設定值跟蹤控制.污水處理過程中，溶解氧的神經網絡預測控制系統結構，如圖2所示.其中包括神經網絡預測模型和神經網絡預測控制器，神經網絡預測模型使用過去時刻的輸入u（k＋p－nu），…，u（k＋p）和輸出y（k＋p－ny），…，y（k＋p－1）數據，通過性能指標函數Jm（k）訓練網絡，并用訓練好的神經網絡逼近模型預測系統未來輸出，神經網絡預測控制器通過最小化誤差代價函數Jc（k）計算Δu（k），與前一時刻控制量u（k－1）相加得到此刻控制量最優輸入KLa，從而控制輸入在未來一段指定時間內將最優化模型性能，使系統實際輸出y（k）不斷接近期望輸出值yr.

圖2 神經網絡預測控制系統結構框圖Fig.2 Structure of neural network predictive control system

2.1 神經網絡預測模型

利用神經網絡辨識系統模型，設該系統可用離散時間模型描述為

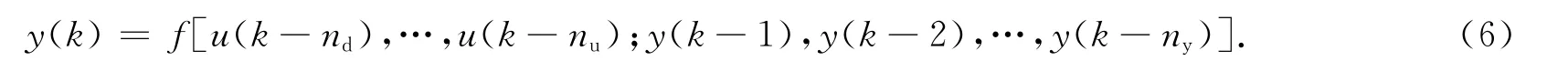
式（6）中：y（k）為系數期望輸出值；nd為系統滯后拍數；nu為用于辨識模型的過去時刻輸入量個數；ny為用于辨識模型的過去時刻輸出量個數；f（·）為非線性擬合函數.利用遞推原理，根據模型（6）可以預測k＋1時刻輸出值，將得到的k＋1時刻的預測值作為預測模型預測k＋2時刻的輸入，重復使用此模型進行前向多步預測，預測下一步時，將之前的預測結果作為預測下一步的輸入.根據模型（6）可以預測k＋p時刻的系統輸出值為

采用三層BP神經網絡訓練f（·），包括輸入層（i個神經元）、隱含層（j個神經元）和輸出層（h個神經元），建立神經網絡模型為

式（8）～（11）中：xs，i（k）為輸入層第i個神經元的輸入；nets，j（k）為隱含層第j個神經元的輸入；uj為隱含層第j個神經元的輸出；ym，h（k）為輸出層第h個神經元的輸出；g（·）為隱含層傳輸函數，這里取S型函數；wi，j為輸入層第i個神經元到隱含層第j個神經元的連接權值；wj，k為隱含層第j個神經元到輸出層第k個神經元的連接權值.

BP神經網絡在辨識過程中根據輸出量誤差按照梯度修正法修正權值，修正權值的過程為

式（13），（14）中：η為預測模型學習率，η＞0.

通過神經網絡的不斷學習更新權值，使預測輸出值不斷接近實際輸出值.由以上分析可得，k＋p時刻的神經網絡學習模型為

式（15）中：u（k），u（k＋1），…，u（k－nd＋p）等參數，用NNPC的預測值代替，如果超出預測范圍，則以最后的預測值代替.

訓練神經網絡的數據來源于污水處理數學模型（1）～（4）.通過實驗可得：當輸入在［0.45，0.95］內時，輸出量即溶解氧濃度可以維持在［1.58，3.97］內，神經網絡初始的學習樣本通過在給定區間［0.45，0.95］內隨機輸入并測定相應輸出的方式獲得.考慮不同單位的數量級差異，在訓練網絡之前，所有數據均須被歸一化處理至區間［0，1］，然后用處理后的數據訓練神經網絡.

通過以上分析，系統辨識只需要建立一個神經網絡，根據系統過去時刻的輸入輸出數據，通過訓練建立系統的單步預測模型，根據式（6），（7），將多個單步模型串聯即可獲得多步預測模型.

2.2 神經網絡預測控制器

采用三層BP網絡建立神經網絡預測控制器，神經網絡預測控制器模型的輸入和輸出分別為

式（17）～（18）中：yr（k）為期望輸出值；nc為控制時域長度.

神經網絡預測控制器模型為

式（19）～（22）中：xcs，i（k）為輸入層第i個神經元的輸入，i＝1，2，…，ny＋p＋1；netcs，j（k）為隱含層第j個神經元的輸入；ucj為隱含層第j個神經元的輸出，j＝1，2，…，nc，j；Uch（k）為輸出層第h個神經元的輸出，h＝1，2，…，nc，h；gc（·）為隱含層S型傳輸函數；wci，j為輸入層第i個神經元到隱含層第j個神經元的連接權值；wcj，h為隱含層第j個神經元到輸出層第h個神經元的連接權值.

權值更新的方式為

式（23）～（24）中：ηc為控制器學習率，ηc＞0.

在實際污水處理系統中，出水水質是最重要的污水處理指標，而排出的底物濃度是出水水質是否達標的主要檢測指標.研究表明，溶解氧濃度控制在1.58～3.97mg·L－1之間，能夠滿足每日排出的底物濃度不大于150kg BOD 的環保要求［10］.因此，研究的溶解氧濃度控制值均約束在此范圍內.考慮上述約束條件，建立神經網絡預測控制器，最小化性能目標代價函數Jc（k），即

式（25）中：Q為誤差權矩陣；R為控制權矩陣；np為預測時域長度；nc為控制時域長度.應用預測控制器（25）來計算Δu（k），與前一時刻控制量u（k－1）相加得到此刻控制量最優輸入KLa，從而輸入控制量在未來一段指定的時間內將最優化模型性能，使系統實際輸出y（k）不斷接近期望輸出值yr.

3 控制系統的仿真分析

以基于活性污泥法ASM1模型為被控對象，在Matlab／Simulink仿真環境中構建污水處理溶解氧神經網絡預測控制系統.在仿真過程中，根據實際情況假設：系統連續運行5d（即120h）內，溶解氧的時變設定值為先由2.0mg·L－1升高到2.5mg·L－1，再恢復到2.0mg·L－1，接著降低到1.7mg·L－1，最后再恢復到2.0mg·L－1.控制系統采樣時間t取為0.1h；神經網絡預測控制器的預測時域長度np＝10；控制時域長度nc＝3，滯后拍數nd＝0，nu＝2，ny＝2；神經網絡預測模型選擇4－6－1結構，神經網絡預測控制器選擇2－5－1結構；神經網絡學習速率為η＝0.2，ηc＝0.5.

3.1 測量白噪音情況下時變設定值的跟蹤控制

假設在溶解氧濃度傳感器反饋信號中加入幅值為0.01的高斯白噪音干擾信號，分別采用傳統PID控制器和神經網絡預測控制器對系統溶解氧濃度（ρDO）進行控制仿真，得到的仿真結果如圖3所示.由圖3分析可知：在測量白噪音干擾下，傳統PID 控制器出現持續振蕩現象，即溶解氧濃度控制波動幅度較大，而神經網絡預測控制器對溶解氧濃度的時變設定值跟蹤控制超調量小，溶解氧濃度跟蹤控制能夠保持平穩狀態，可有效實現對溶解氧濃度的時變設定值跟蹤控制.

3.2 進水流量發生階躍變化情況下時變設定值跟蹤控制

假設系統在30h時給進水底物質量濃度（Sin）加入大小為50mg·L－1的階躍干擾，在80h時給Sin加入大小為－100mg·L－1的階躍干擾，在系統控制器各參數均保持不變的前提下，分別采用傳統PID控制器和神經網絡預測控制器對系統溶解氧濃度（ρDO）進行控制仿真，得到仿真結果如圖4所示.由圖4分析可知：在進水流量發生階躍干擾下，神經網絡預測控制器對溶解氧濃度的時變設定值跟蹤控制引起的超調量小，且能較快恢復到穩定狀態，而傳統PID 控制器則出現較大超調量.

圖3 測量白噪音情況下的仿真結果Fig.3 Simulation results with white noises in the DO concentration measurements

圖4 進水流量發生階躍變化情況下的仿真結果Fig.4 Simulation results with step disturbances in the influent

3.3 控制性能的量化比較

由圖3和圖4可以明顯看出：對于溶解氧濃度的時變設定值跟蹤控制，與傳統PID 控制器相比較，神經網絡預測控制器調節時間短、超調量較小，動態響應速度快，顯示了該控制器的有效性和優越性.采用IAE，ISE作為兩個積分型性能指標來對控制性能進行測試與量化評價，它們分別定義為

通常較小的IAE或ISE指標代表更好的控制性能.性能指標量化結果，如表1所示.由表1可知：在不同干擾情況下，神經網絡預測控制方法相比于傳統PID 控制方法，IAE 和ISE 指標均分別有較大幅度的減小，系統控制性能得到有效改進.

表1 不同控制方法系統性能的比較Tab.1 Comparisons of system performance for different control methods

4 結束語

基于活性污泥法污水處理ASM1模型，考慮若干約束條件，設計出神經網絡預測控制器，有效實現了污水處理過程溶解氧濃度的時變設定值跟蹤控制，并研究了溶解氧濃度傳感器測量白噪音和進水流量發生階躍變化兩種干擾情況對溶解氧濃度跟蹤控制性能的影響.仿真實驗結果表明：針對污水處理溶解氧濃度的時變設定值跟蹤控制，考慮外界干擾因素，與傳統PID 控制器相比，神經網絡預測控制器超調量減小，響應快速，明顯改善了系統動態控制性能，抑制干擾能力增強，有良好的自學習能力和適應性，為解決污水處理溶解氧濃度時變設定值跟蹤控制問題提供了一條很好的途徑.

［1］HENZE M.Activated sludge models ASM1，ASM2，ASM2dand ASM3［M］.London：IWA Publishing，2000：13－15.

［2］KATEBI M R，JOHNSON M A，WILKE J.Control and instrumentation for wastewater treatment plant［M］.London：Springer－Verlag，1999：38－41.

［3］NEJJARI F，BENHAMMOU A，DAHHOU B，et al.Non－linear multivariable adaptive control of an activated sludge wastewater treatment process［J］.Int J Adapt Control Signal Process，1999，13（5）：347－365.

［4］張平，苑明哲，王宏.基于國際評價基準的溶解氧控制方法研究［J］.信息與控制，2007，36（2）：199－203.

［5］TZONEVA R.Optimal PID control of the dissolved oxygen concentration in the wastewater treatment plant［C］∥IEEE AFRICON Conference.Windhoek：IEEE Press，2007：1－7.

［6］CHEN J C，CHANG Ni－bin.Mining the fuzzy control rules of aeration in a submerged biofilm wastewater treatment process［J］.Engineering Applications of Artificial Intelligence，2007，20（7）：959－969.

［7］甄博然，韓紅桂，喬俊飛.基于增長型神經網絡的污水處理過程溶解氧控制［J］.中南大學學報：自然科學版，2009，40（1）：74－79.

［8］王小藝，李萬東，劉載文，等.一種模糊PID－Smith污水處理的控制方法［J］.計算機與應用化學，2010，27（6）：801－803.

［9］付文韜，武利，王莉莉，等.神經網絡PID 的溶解氧控制系統［J］.計算機與應用化學，2013，30（10）：1135－1138.

［10］胡玉玲，曹建國，喬俊飛.活性污泥污水處理系統的模糊神經網絡控制［J］.系統仿真學報，2005，17（10）：2541－2544.

［11］SHEN Wen－hao，CHEN Xiao－quan，PONS M N，et al.Model predictive control for wastewater treatment process with feedforward compensation［J］.Chemical Engineering Journal，2009，155（1／2）：161－174.

［12］CRISTEA S，DEPRADA C，SARABIA D，et al.Aeration control of a wastewater treatment plant using hybrid NMPC［J］.Computers and Chemical Engineering，2010，35（4）：638－650.

［13］劉載文，張春芝，王小藝，等.基于遺傳算法的污水處理過程優化控制方法［J］.計算機與應用化學，2007，24（7）：959－962.

［14］HOLENDA B，DOMOKOS E，REDEY A，et al.Aeration optimization of a wastewater treatment plant using genetic algorithm［J］.Optimal Control Applications and Methods，2007，28（3）：191－208.

［15］孫增圻，張再興，鄧志東.智能控制理論與技術［M］.2版.北京：清華大學出版社，2011：123－126.

［16］CAMACHO E F，BORDONS C.Model predictive control.advanced textbooks in control and signal processing［M］.2nd.London：Springer－Verlag，2004：3－9.