從雙視圖到多視圖的協同優化立體視覺匹配算法

王道累，吳懋亮，陳軍

（上海電力學院 能源與機械工程學院，上海200090）

20世紀80年代，Marr等［1］提出了一種使計算機通過二維圖像恢復三維場景信息的能力視覺計算理論，并應用在雙目或多目匹配上，從而奠定了雙目或多目立體視覺發展的理論基礎.立體匹配是計算機視覺關鍵技術之一，現有解決立體匹配問題的算法主要分為兩類：基于局部約束的算法和基于全局約束的算法［2－4］.Wu等［5］采用張量投票算法對PMVS中的特征擴展和噪聲過濾進行優化.Nguyen等［6］提出局部稠密解碼方法，利用45°和90°兩方向對該方法進行求導，獲得視差圖.Xu等［7］提出優化局部自適應算法，求解圖像對視差.上述算法都是基于局部算法求解視差，但這類算法對圖像噪聲較敏感，對重復紋理區域、遮擋區域和視差不連續區域等往往匹配效果不理想，錯誤匹配率較高.在此基礎上，很多計算機視覺研究專家提出基于全局約束算法，對整個圖像數據信息進行計算，這樣降低對局部區域敏感度，解決重復紋理的影響，同時，也可以求解視差不連續區域，最終達到全局最優解.基于全局優化算法的本質是把匹配問題轉化為求解能量函數，然后，通過求解該能量方程的全局最優解，并可尋找到匹配點.全局算法一般有動態規劃算法、圖割算法［8］和人工智能算法等.本文研究雙視圖到多視圖立體匹配算法，提出基于全局協同算法解決多視圖的匹配問題，從而準確獲得并恢復三維場景深度.

1 雙目立體視覺匹配

1.1 圖像分割

在圖像分割之前，通過兩個假設：每個分割區域內的視差值變化細微，平滑過渡；只有在分割區域邊界存在深度距離的不連續性.采用mean－shift算法［9］對參考圖像（兩幅圖像任選一副作為參考圖像）進行分割，能很好滿足圖像的匹配假設條件.

1.2 視差的初始化

由于局部匹配算法速度快、運算簡單，局部匹配算法被用來計算視差初始值，采用自適應相似算法來計算雙視圖匹配視差值.自適應相似算法具體表示為

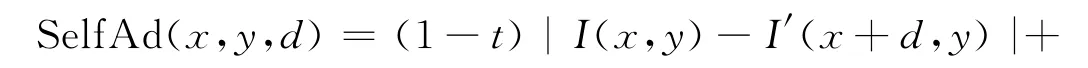
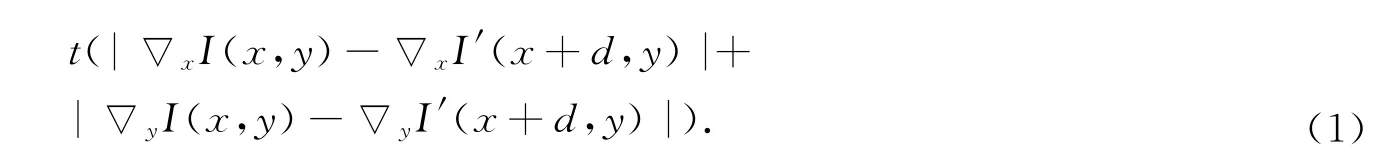
式（1）中：I和I′分別代表左右圖像中像素坐標（x，y）處的灰度；t表示灰度值差和梯度差之間的權值.視差值初始化代價方程為

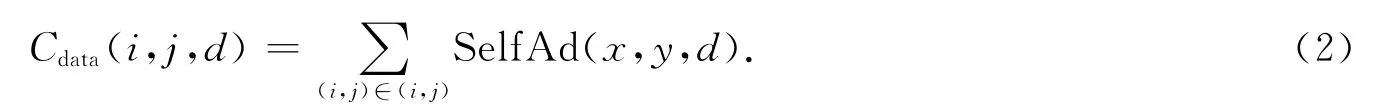
N（x，y）是以像素的（x，y）為中心5×5的矩形窗，使用WTA（winner－takes－all）方法最小化代價方程，求得像素點（x，y）的視差值.

1.3 視差圖平面擬合

在參考圖像分割之后，以分割區域為單位進行視差圖平面擬合.由于假設在同一個分割區域內沒有太大視差變化，所以分割區域內每一個像素的視差可以用一個模型來表示.Tao等［10］給出了視差圖平面的擬合方程，每一個分割區域視差模型表示為

式（3）中：a，b，c是平面的參數；d是像素點（x，y）相對應的視差值.

對于分割區域內的各個像素點可以表示為

式（4）中：矩陣A第i行為［xi，yi，1］；向量B第i行為d（xi，yi）.

對線性方程（4）進行變換，可得

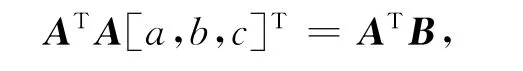
即有

通過奇異值（singular value decomposition，SVD）求解，有

一般情況下，線性方程（5）的對奇異點非常敏感，所以要對奇異點進行排除.這里制定3種規則來排除奇異點.

1）視差相互比較.對左右視圖分別通過自適應相似算法就得視差圖，然后進行相互比較.給定一個誤差閾值ξ，如果小于該閾值ξ，該像素點為可靠的像素點.

2）可靠區域判斷.在排除奇異點之后，分割區域內的可靠像素點總數是否可以到達構建擬合平面的要求，即構成可靠區域.這里規定可靠像素點總數是整個區域像素點數一半以上.

3）視差距離判斷當前獲得視差值與前一次獲得值進行比較，在規定的誤差范圍內，該像素點為可靠像素點.

通過判斷之后，當前獲得平面參數與前一次獲得值進行比較，即

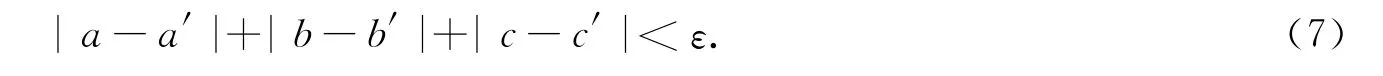
如果在規定的誤差內，循環結束，或者繼續進行參數優化.

1.4 視圖協同優化視差值

視圖協同優化是將一個復雜目標分解為一些相對簡單子目標，相連區域對該子目標影響進行優化［11］.通過mean－shift分割后視圖，如圖1所示.圖1中：s1，s2，…，sn為分割區域.設E（x）為整幅圖像的能量方程，根據協同優化原理，有

式（8）中：Ej（x）（j＝1，2，…，n）是第j個分割區域的能量方程.

將一個復雜的能量分解為相對簡單的子能量方程，通過迭代方程，有

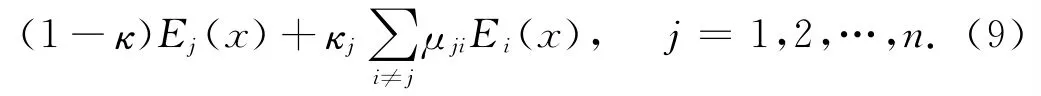
式（9）中：Ei（x）表示第i個分割區域的能量方程，分割域sj（j＝1，2，…，n；i≠j）是分割域sj的相連域；0≤κj≤1，0≤μj，1≤1分別是相對應的權值.

利用協同原理來優化視差值，首先要構建視差擬合區域的能量方程，該能量方程有三部分組成分別是代價方程、懲罰方程和平滑度方程，具體表示為

上式中的各項可分別表示為：

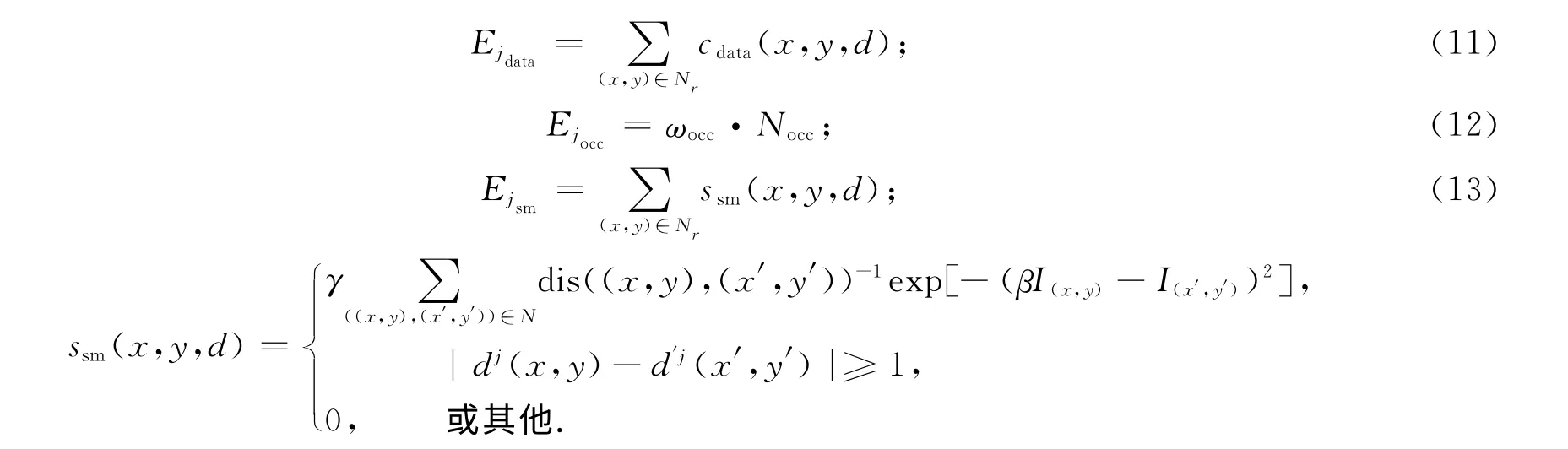
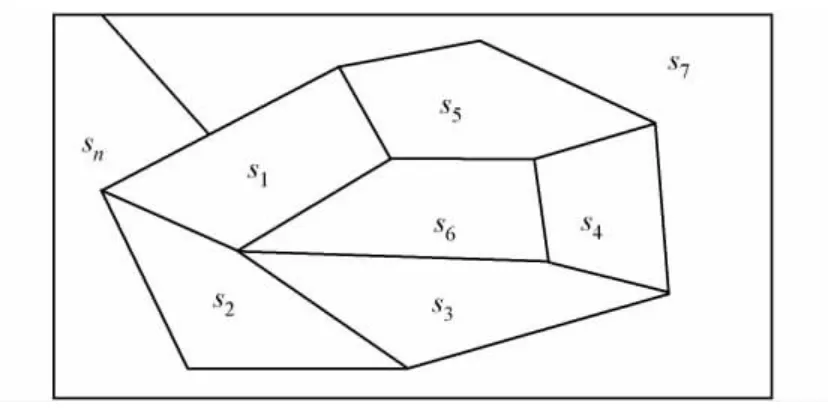
圖1 通過mean－shift分割后視圖Fig.1 Segmented reference image

各個參數定義如下：cdata（x，y，d）的定義同節1.2；ωocc為遮擋懲罰系數；Nocc為區域內遮擋像素數（通過上面3個規則判斷得到的不可靠像素數）；Nr是可靠區域像素集；I（x，y）和I（x′，y′）分別是像素點（x，y）和（x′，y′）的灰度；N以像素的（x，y）為中心5×5的矩形窗；dis（·）是兩像素點歐幾里得距離；γ是一個常數；β定義為

最后，通過Powell方法求解能量方程（9），獲得第j個分割區域的最優視差平面參數（aj，bj，cj），就可以獲得優化后視差圖.

2 多目立體視覺匹配

利用多視圖進行立體匹配求視差，給匹配算法提供更多的信息.有利于提高算法的精度，降低匹配的錯誤率.選擇其中一幅為參考圖像，該參考圖像與其他圖像進行兩兩匹配求得視差圖，形成了多個視差集（d（1），d（2），…，d（n）），如何優化合并這一系列視差集將是多視圖匹配的關鍵問題之一.

雙視圖立體算法有3個匹配步驟.

步驟1對參考圖像進行分割.

步驟2采用自適應相似算法求初始化視差，并求得（d（1），d（2），…，d（n））.

步驟3利用視差平面擬合對多視圖視差集進行合并.

對于多視圖視差平面擬合，平面模型表示為

式（15）中：第j個分割域在第i個視差集中的模型.

對多視差集合并，參考圖像第j個分割域和其他圖像所形成視差，其區域內各個像素點的線性方程表示為

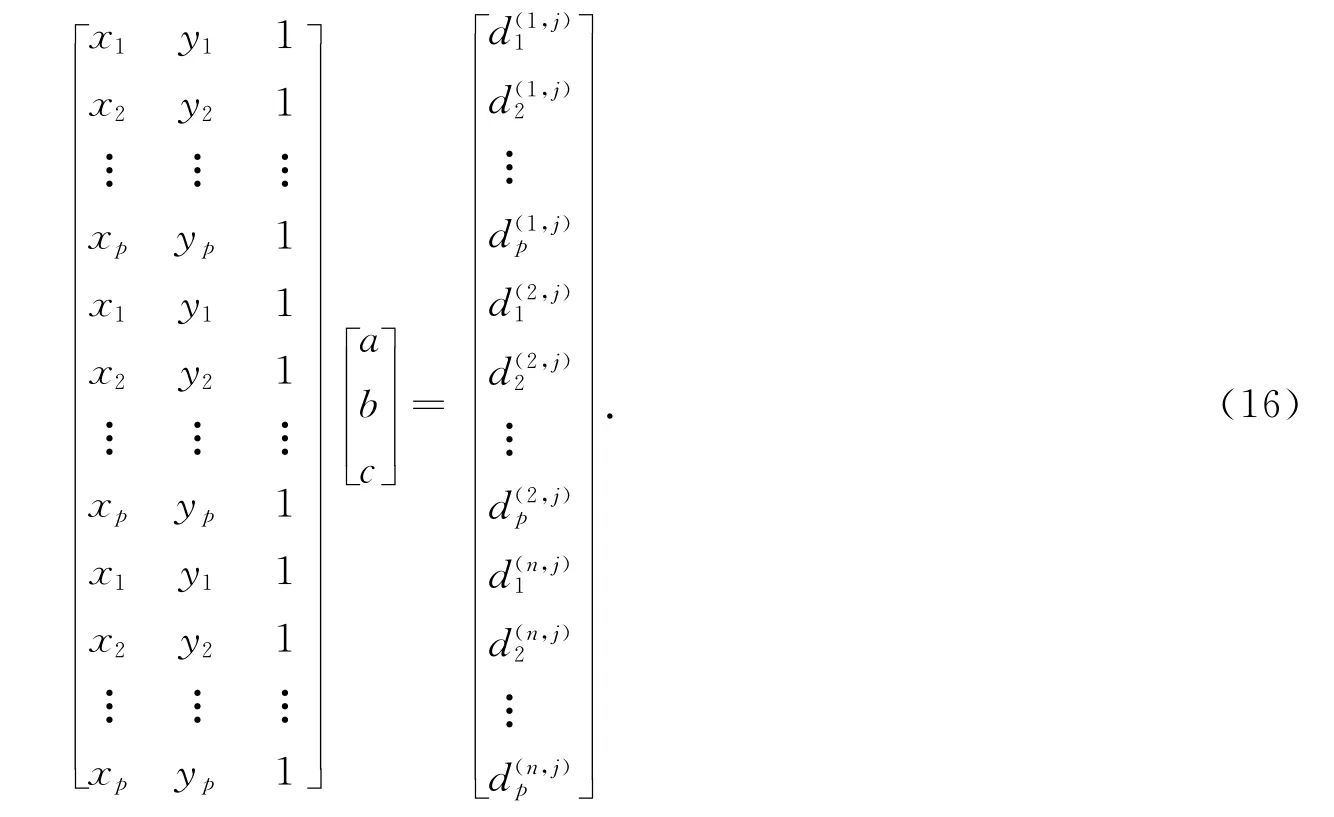
式（16）中：p是在第j個分割域中像素點個數；是第i個視差集的第j個分割域中第k個像素點的視差值（i＝1，2，…，n；j＝1，2，…，m和k＝1，2，…，p）；a，b，c是第j個分割域的擬合平面系數.

從方程（16）獲得到第j個分割域的擬合視差值是各個視差集中該分割域的平均值，奇異值分解得到視差擬合平面的系數，即

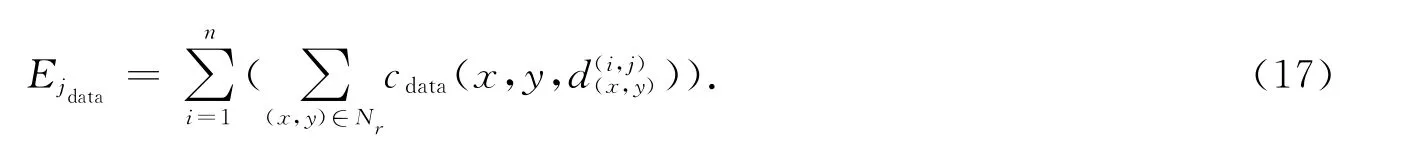
以此類推，可以對參考圖像的其他分割域進行同樣平面擬合，最后獲得整副參考圖像的視差圖.

線性方程（16）進行奇異點的排除，同理，應用雙目視圖匹配的規則判斷獲得可靠分割區域.采用協調優化方法對多視圖視差進行優化，多視圖能量方程的建立，具體定義為雙目視圖匹配（方程10），各個部分具體定義為

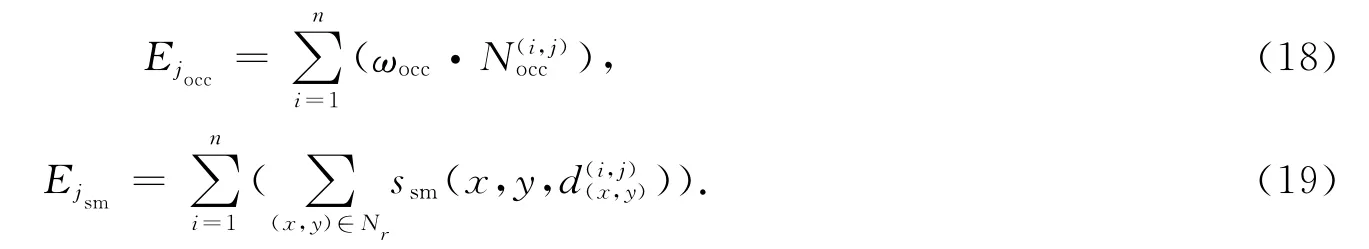
各個參數定義如雙視圖匹配能量方程，同理，根據方程（9）定義，利用Powell算法迭代優化得到最優多視圖視差.

3 實驗結果及討論

3.1 匹配算法流程圖

算法具體表述為如下5個步驟.

步驟1視圖組輸入.

步驟2選擇參考圖像進行分割處理.

步驟3運用局部自適應相似算法計算初始化視差.

步驟4視差平面擬合，并根據規則排除奇異點建立可靠區域集.

步驟5利用協同優化視差平面參數獲得最優視差值.

3.2 實驗結果

對述的匹配算法的流程圖進行運算，雙視圖及多視圖的視差圖采用Middlebury［10］的視圖Tsukuba，Venus，Cones和Teddy，運行結果如圖2所示.圖2（a）為原始圖（Tsukuba，Venus，Cones和Teddy），圖2（b）為對應的ground－truth圖，圖2（c）為建議的雙視圖匹配算法結果圖.

通過執行協同優化匹配算法獲得Tsukuba，Venus，Cones和Teddy的多視圖視差圖，如圖3所示.

圖2 雙視圖視差圖Fig.2 Disparity map of binocular stereo matching

各雙視圖及多視圖的算法結果，如表1所示.表1中：η為錯誤匹配率.由表1可知：利用協同優化匹配算法對多視圖獲得錯誤匹配率最小，雙視圖次之，局部算法獲得的初始化視差錯誤率最大.這樣也充分說明了多視圖能提高更多信息，有利于算法改進，減少錯誤的匹配.局部算法對圖像匹配比較敏感，速度雖快，單精確度劣于全局的匹配算法.同時，也比較了GF［13］，ST－1［14］的雙視圖錯誤匹配率.結果表明：匹配算法是可以獲得較好的匹配數據，但在參考圖Cones上，算法表現不夠好，需要對處理遮擋問題作進一步優化.

圖3 多視圖視差圖Fig.3 Disparity map of multi－ocular stereo matching

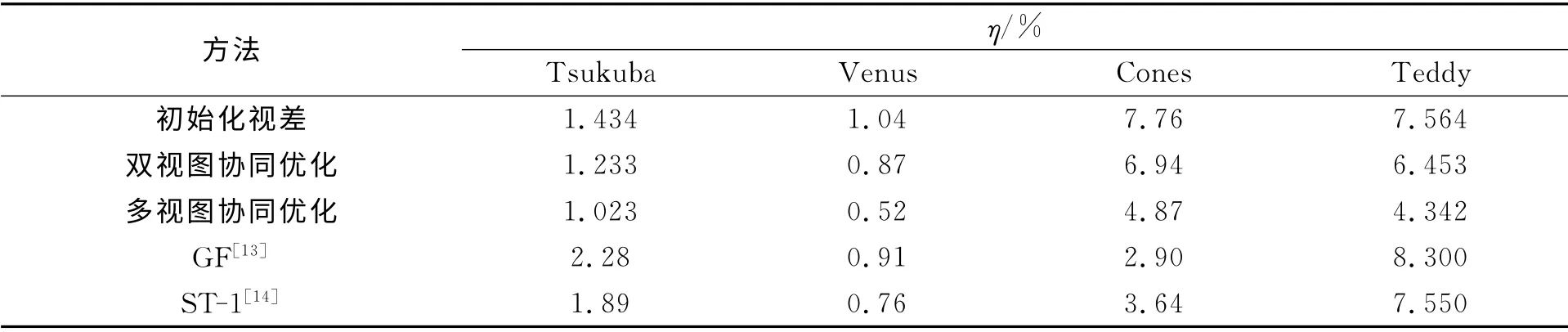
表1 各方法求得視圖差比較Tab.1 Compare with results of stereo matching methods

4 結束語

研究立體視覺匹配算法，利用協調優化對雙視圖及多視圖進行匹配優化.利用SVD 方法對線性方程進行求解，同時，在多視圖在通過視差平面擬合合并視差集.制定排除奇異點的規則，能很好判斷遮擋及非可靠像素點.本算法不僅可以解決雙視圖匹配問題，也可以推廣到多視圖立體匹配問題的解決.今后，將對算法進一步改進及提出更好的平面擬合算法.

［1］MARR D，POGGIO T.A computational theory of human stereo vision［C］∥Proceedings of the Royal Society of London.London：IEEE Press，1979：301－328.

［2］FAUGERAS O，LONG Q.The Geometry of multiple images［M］.Cambridge：Cambridge University Press，2001：1－50.

［3］FURUKAWA Y，PONCE J.Accurate，dense，and robust multi－view steropsis［J］.IEEE Transaction on Pattern Analysis and Machine Intelligence，2010，32（8）：1362－1376.

［4］LHUILLIER M，QUAN Long.Aquasi－dense approach to surface reconstruction from uncalibrated images［J］.Transactions on Pattern Analysis and Machine Intelligence，2005，27（3）：418－433.

［5］WU Tai－pang，YEUNG S K，YA Jia－jia，et al.Quasi－dense 3Dreconstruction using tensor－based multi－view stereo［C］∥Computer Society Conference on Computer Vision and Pattern Recognition.San Francisco：IEEE Press，2010：1482－1489.

［6］VINH D N，DUC D N，SANG J L，et al.Local density encoding for robust stereo matching［J］.IEEE Transctions on Circuits and Systems for Video Technology，2014，24（12）：2049－2062.

［7］XU Ling－feng，OSCAR C A，SUN Wen－xiu，et al.Stereo matching with optimal local adaptive radiometric compensation［J］.IEEE Signal Processing Letters，2015，22（2）：131－135.

［8］WANG Dao－lei，LIM K B.Obtaining depth map form segment－based stereo matching using graph cuts［J］.Journal of Visual Communication and Image Representation，2002，24（5）：603－619.

［9］COMANICIU D，MEER P.Mean shift：A robust approach toward feature space analysis［J］.Transactions on Pattern Analysis and Machine Intelligence，2002，24（5）：603－619

［10］TAO H，SAWHNEY H S，KUMAR R.A global matching framework for stereo computation［C］∥International Conference on Computer Vision.Vancouver：IEEE Press，2001：532－539.

［11］HUANG Xiao－fei.Cooperative optimization for energy minimization：A case study of stereo matching［EB／OL］.［2014－09－23］.http：／／front.math.ucdavis.edu／author／X.Huang，cs.CV／071057.

［12］BLAKE A，ROTHER C，BROWN M，et al.Torr，interactive image segmentation using an adaptive GMMRF model［C］∥Proceedings European Conference of Computer Vision.Prague：Czech Republic，2004：428－441.

［13］RHEMANN C，HOSNI A，BLEYER M C，et al.Gelautz fast cost－volume filtering for visual correspondence and beyond［C］∥Conference on Computer Vision and Pattern Recognition.Colorado Springs：IEEE Press，2011：3017－3024.

［14］MEI Xing，SUN Xun，DONG Wei－ming，el at.Segment－tree based cost aggregation for stereo matching［C］∥IEEE Conference on Computer Vision and Pattern Recognition.Portland：IEEE Press，2013：23－28.