基于梯度強度立柱的客車側翻安全性多目標優化設計

周莎，張勇，張成，李奇

（華僑大學 機電及自動化學院，福建 廈門361021）

客車側翻事故是特大交通事故的主體.客車因其所載乘客較多，經常出現群死群傷的現象，造成惡劣的社會影響.因此，對客車側翻安全性進行研究具有重要意義［1］.為了更好地研究客車側翻事故，國內外都相繼出臺了客車側翻實驗的法規，較典型的是歐洲的ECE R66法規，GB 17578－2013《客車上部結構強度要求及試驗方法》詳細地規范了客車上部結構強度要求和相關的試驗方法［2－3］.對于客車側翻安全性的研究，Su等［4］基于代理模型，利用響應面來實現客車多目標優化；Liang等［5］通過優化每根立柱厚度來改善客車上部結構強度和吸能性；高云凱等［6］基于客車上部結構關鍵零部件截面形狀進行側翻安全性多目標優化.然而，這些研究并未考慮到側翻過程中側圍立柱不同位置受力不均勻的特點.本文針對這一現象提出一種新型的梯度強度立柱結構，使立柱不同位置的強度與受力匹配，從而減小側圍的擠壓變形，提高側翻安全性.

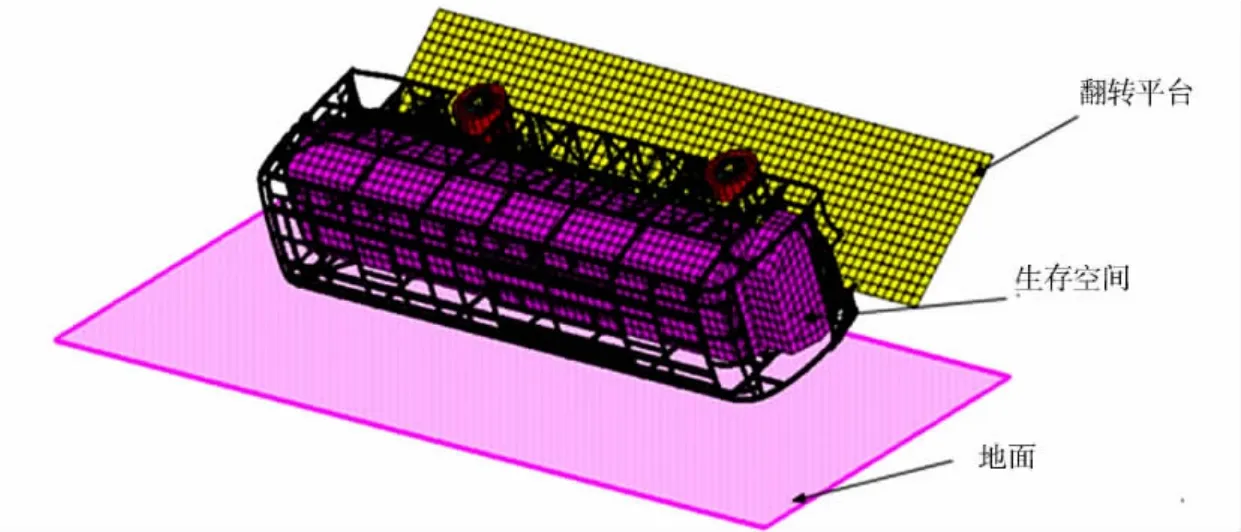
圖1 客車側翻有限元模型Fig.1 Bus rollover finite element model

1 客車有限元模型的建立

以某型號全承載大客車為研究對象，并建立該客車的有限元模型，如圖1 所示.模型主要包括車身骨架、底架和車輪等.其他部件如發動機、油箱、蒙皮和座椅等均以集中載荷或均布載荷等效配重的方式加載到對應幾何位置的節點上，保證整車有限元模型的質心高度位置和實車的基本吻合，誤差控制在2%以內［7］.基于ECE R66法規建立的客車有限元側翻模型，其主要包括車身部分、翻轉平臺和地面.并且，為方便評價客車上部結構的強度及安全性，模型依據ECE R66定義了乘員的生存空間.

為了保證乘員安全性，客車側翻過程中車身部件不能侵入生存空間.整車有限元模型共有412 967個單元，419 535個節點.車身骨架的材料為Q345，密度為7 800kg·m－3；彈性模量為210GPa；泊松比為0.3；屈服極限為345 MPa.

2 客車側翻安全性分析及驗證

建好的客車側翻有限元模型采用LS－DYNA 進行數值仿真分析，整個分析過程從客車撞地瞬間到車身完全離開地面為止，歷時250ms.側翻碰撞過程中車身與地面的撞擊力，如圖2所示.由圖2可知：整個過程有兩個波峰值，從開始到0.008s時車身結構與地面發生撞擊，此時撞擊力達到最大值1 570 kN；到0.078ms左右時碰撞力達到另一個峰值551kN，此時車身變形量達到最大；到0.215s后，碰撞力幾乎為零，說明此時車身開始彈離開地面.

碰撞過程中的能量曲線，如圖3所示.由圖3可知：整個過程能量守恒，沙漏能所占比例小于5%.為驗證該有限元模型的有效性，結合與該車型結構相近的對標車型的側翻實驗，進行對比分析，結果如表1所示.表1中：側翻過程中側圍每根立柱與生存空間的最小距離（入侵量）分別為D1，D2，D3，D4，D5，D6，D7.由表1可知：對標模型的側翻初始侵入與當前模型較為吻合，因此，可認為整車模型和分析都是合理、可靠的［8］.

側翻碰撞過程中在立柱上間隔均勻選取5個測試點，側圍立柱的應力云圖，如圖4所示.由圖4可知：側翻過程中其立柱不同位置的應力水平差別較大.

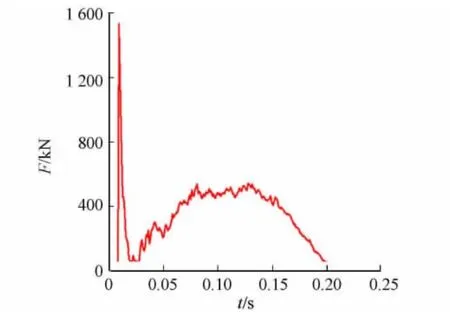
圖2 撞擊力曲線 Fig.2 Impact force curve

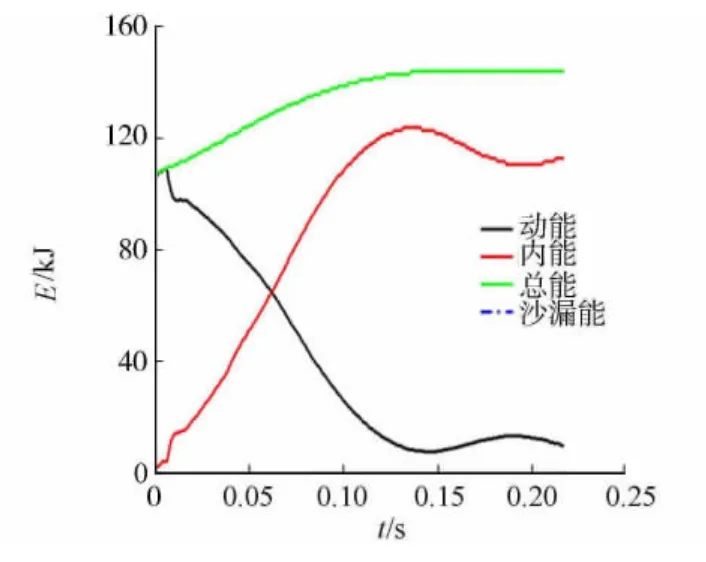
圖3 車身能量曲線Fig.3 Body energy curve

表1 對標模型與當前模型側翻入侵對比Tab.1 Rollover invasion comparison of simulation and experiment model

側翻過程中車身結構最大變形，如圖5所示.由圖5可知：碰撞過程中，生存空間明顯被入侵，不滿足ECE R66法規要求，因此，需要強化車身上部結構強度來提高客車側翻安全性能.

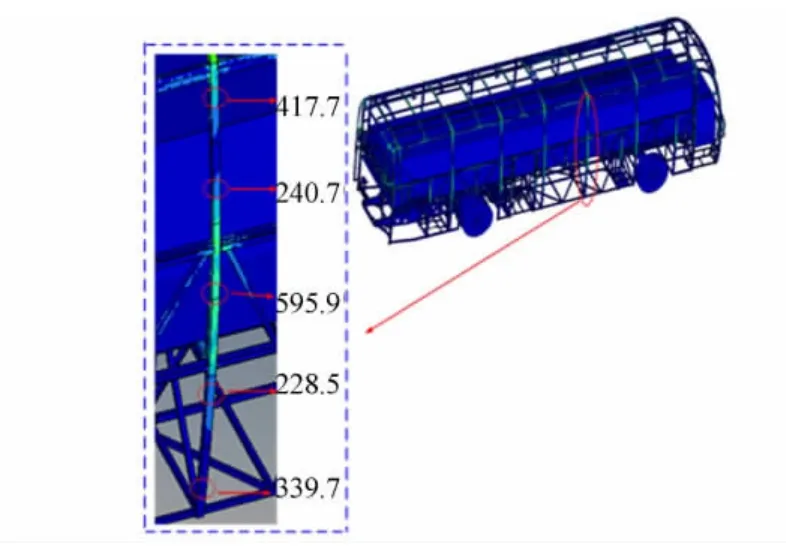
圖4 側圍立柱的應力云圖Fig.4 Stress nephogram of side wall pillar（MPa）

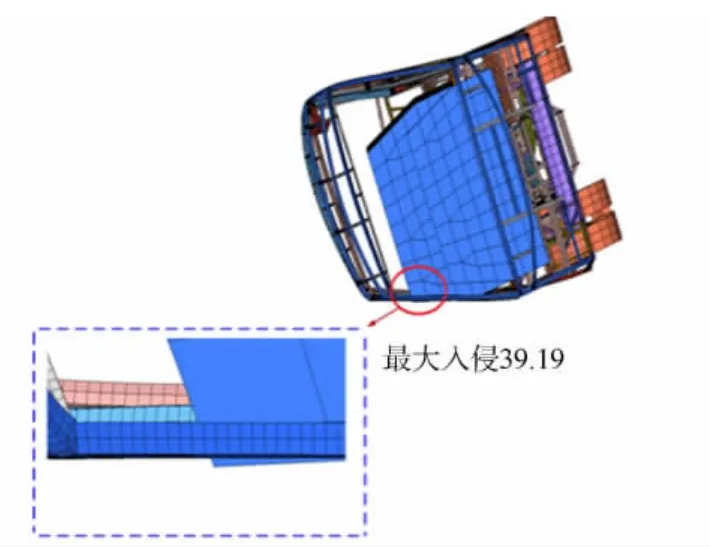
圖5 側翻入侵示意圖Fig.5 Schematic view of rollover invasion（mm）

3 梯度強度立柱結構側翻安全性的優化

3.1 設計流程的優化

從客車側翻過程可以看出：側圍立柱是關鍵的承力部件，側翻碰撞過程中客車立柱不同位置受力相當不均勻.因此，提出了一種新型的梯度強度立柱結構，使立柱不同位置的強度與受力匹配，從而減小側圍的擠壓變形，提高側翻安全性.為了進一步使立柱結構強度分布更加合理，基于客車梯度強度立柱的強度匹配進行客車側翻安全性的多目標優化流程，如圖6所示.

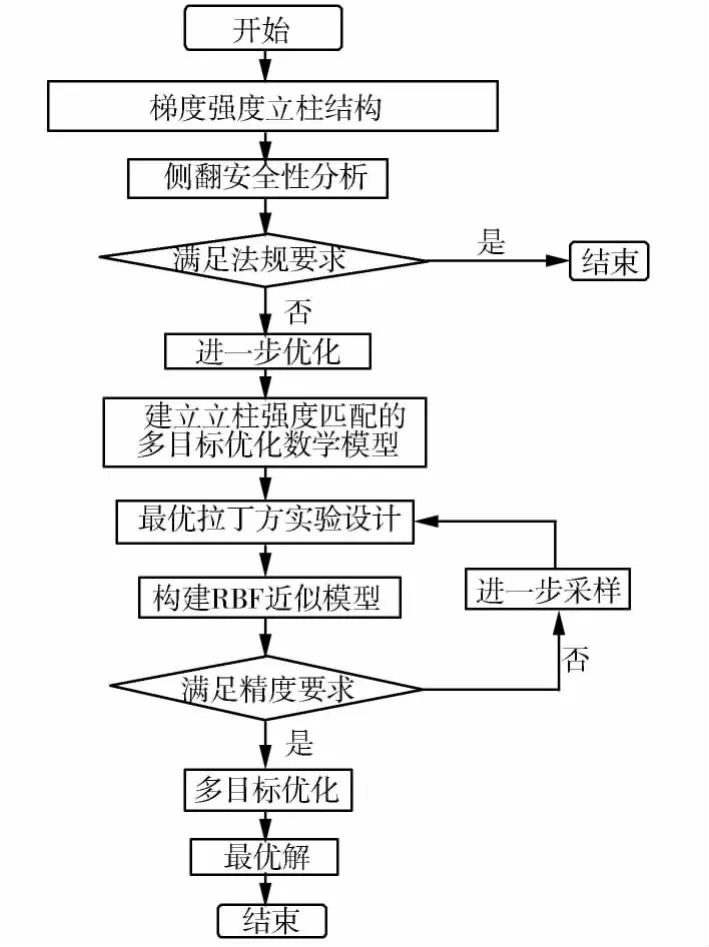
圖6 客車車身多目標優化設計流程圖Fig.6 Design flow chart of bus body multi－objectiveoptimization design flow

3.2 梯度強度立柱結構及側翻分析

客車梯度強度立柱結構是把立柱均勻分為6單元，每個單元強度不一樣，且呈梯度變化，客車側圍梯度強度立柱結構示意圖，如圖7所示.

采用熱成型方法［9－10］加工的梯度強度立柱結構，如圖8所示.該結構將客車每根立柱均勻分為6 個單元：Q1，Q2，Q3，Q4，Q5，Q6，6個單元的強度沿高度變化.根據熱成型的梯度強度立柱結構具有5種屈服強度，6個單元對應的屈服強度為400，500，650，800，1 000，1 000 MPa.

為了驗證梯度強度結構的性能，將初始客車立柱替換為梯度強度立柱，對其進行數值仿真分析，得到的各立柱對生存空間的入侵量，如表2所示.表2中：負數表示有入侵情況.由表2可知：相對于原始模型的側翻，采用梯度強度立柱結構后的安全性有了明顯提高，但立柱對生存空間還有一定的侵入量，因此，仍需要對其進行的優化設計.

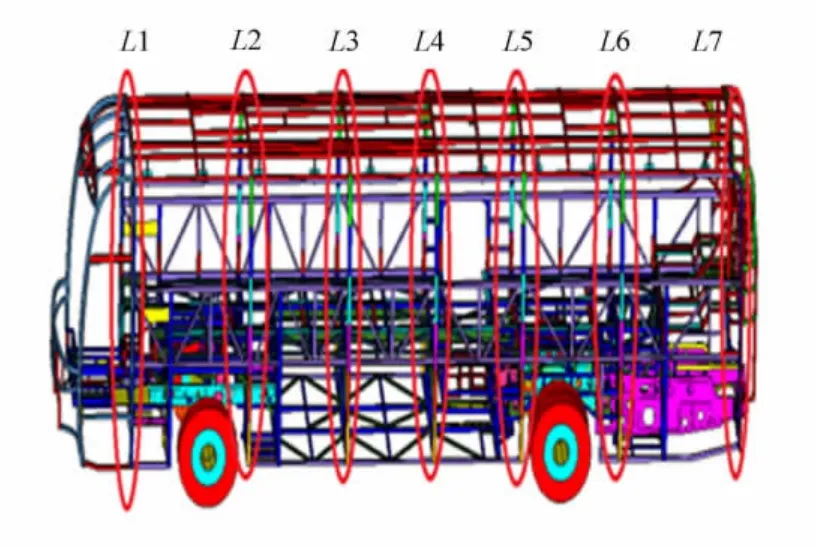
圖7 客車側圍立柱結構示意圖Fig.7 Bus side wall pillars structure

圖8 梯度強度立柱結構Fig.8 Gradient strength pillar structure

表2 立柱對生存空間入侵量Tab.2 Pillar on the amount of living space invasion

3.3 客車側翻多目標優化數學模型

雖然單目標優化能夠改善設計性能，但單目標優化在復雜的設計要求下不能為設計師提供多種可選的設計方案［11］.在汽車優化設計中應該綜合考慮汽車各方面因素，實現汽車更多性能要求.多目標優化不同于單目標優化，最后所得的最優解不是唯一解，而是一個Pareto最優解集或Pareto前沿.求解多目標問題實質就是尋求Pareto最優解集的過程［12］.

客車側翻過程中，乘客受傷害有兩種主要形式［13］：被入侵的生存空間對乘客進行的擠壓，乘客與車體之間的二次碰撞.因此，為降低客車側翻時對乘客的傷害，以客車梯度強度立柱結構為優化對象，選取立柱6個單元的屈服強度和每根立柱厚度做為設計變量，以生存空間的侵入量為設計約束，以側翻碰撞后車身吸收能量和立柱質量為設計目標，建立基于梯度強度立柱結構強度匹配的客車車身多目標優化數學模型，即

式（1）中：E為側翻中車身吸收的能量；M為立柱結構質量；Q1，…，Q6為立柱結構6個單元的屈服強度；t1，t2，…，t7為對應的每根立柱厚度；立柱厚度下限tj，l為1.5mm，上限tj，h為3.5mm；Di為入侵量.

3.4 近似模型的建立

在工程優化問題中，對于一些高度非線性問題，如汽車碰撞分析等，直接利用有限元模型進行優化迭代過程非常耗時.因此，近似模型技術得到了廣泛的關注和應用.由于徑向基近似模型（radial basis function，RBF）針對客車側翻碰撞這類高度非線性問題有較好的預測精度和穩健性，因此，基于RBF徑向基方法構建了各個響應的近似模型.近似模型的建立包括實驗設計采樣和近似模型技術兩方面［14］.

3.4.1 最優拉丁方實驗設計 最優拉丁方采樣方法能使采樣點比較均勻地分布在采樣空間，是一種“充滿空間”采樣技術，用較少的試驗點就能真實地反映采樣空間信息的特點［15］.因此，對客車梯度強度立柱結構6個單元的屈服強度（Q1，…，Q6）和每根立柱厚度（t1，t2，…，t7）進行了60次最優拉丁方采樣.

3.4.2 RBF近似模型 RBF是以徑向函數為基函數，通過線性疊加的方式構造出來的模型.一般情況下任何函數都可以表示為一組基函數的加權和，可以實現從樣本輸入到基函數輸出之間的一種非線性映射關系［16］，其基本數學表達式為

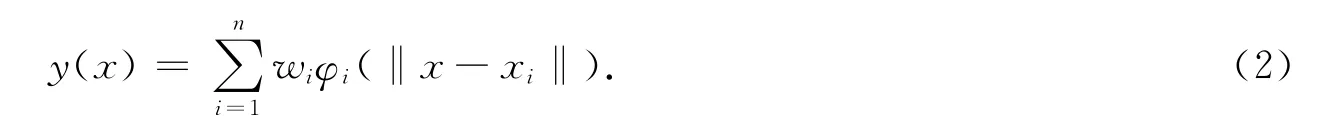
式（2）中：x為設計變量；n為樣本點個數；wi為線性疊加權系數；‖x－xi‖為對應預測點和第i個樣本點之間的歐氏距離；徑向函數為φi（‖x－xi‖）.

3.4.3 近似模型的精度檢查 近似模型的精度決定了最優結果的可行性，因此，必須開展近似模型精度的驗證.采用工程中常用的復相關系數R2檢測，R2定義［17］為

式（3）中：n為樣本數；為第i個樣本點的近似模型預測值；yi為第i個樣本點的真實值（有限元計算值）；為樣本均值.

R2的值在0到1之間，R2越接近1，則表明近似模型的精度越高.通過驗算，基于最優拉丁方樣本點與RBF近似技術得到的各近似模型的R2值，如表3所示.

由表3可知：所有近似模型的R2值都較接近1，說明近似模型的精度都比較高，可用它來代替有限元模型進行多目標優化.

表3 設計響應的近似模型精度Tab.3 Approximate model accuray cof design responses

部分響應的高精度RBF近似模型，如圖9所示.

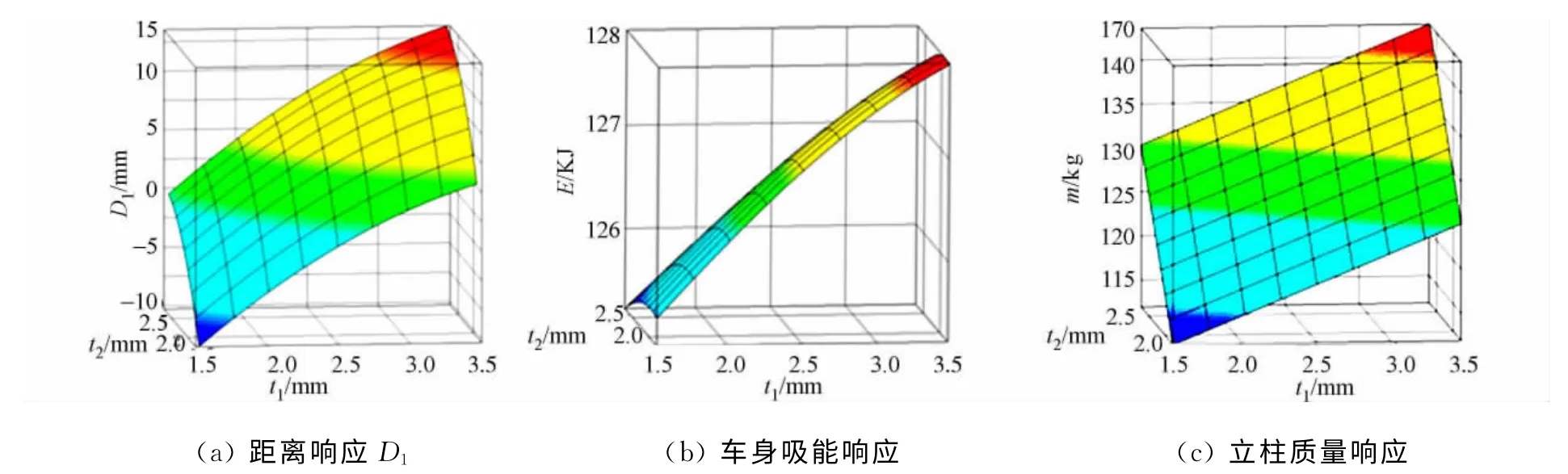
圖9 部分響應近似模型Fig.9 Approximate model of partial response

4 優化結果與討論

采用NSGA－Ⅱ對各個響應的近似模型進行多目標尋優，質量與能量吸收之間的Pareto前沿曲線，如圖10所示.Pareto前沿是一個優化解集，相對單目標優化而言，它能為工程設計人員提供更多的設計方案，常根據設計的實際需求和經濟性來選取最優設計方案.圖10中：紅色標記為在Pareto前沿曲線間隔均勻選取的3組解.

3組最優設計變量所對應響應值，如表4所示.由表4可知：3組皆滿足ECE R66法規的要求；解1 側重于車身減重；解2兼顧車身減重和能量吸收；解3側重于能量吸收.綜合兼顧吸能和輕量化的目的，最后決定以解2為最終解.

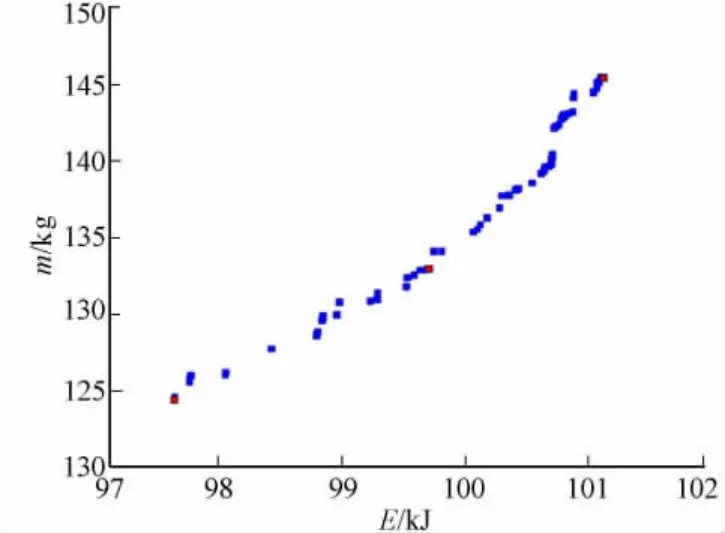
圖10 設計目標的Pareto前沿Fig.10 Pareto front of design objectives

表4 3組Pareto最優解對應的響應值Tab.4 Three groups of Pareto optimal solutions corresponding response

由于優化后整車重量減輕，側翻時初始能量減小及車身變形減小，車身吸能比優化前減少了，而乘客與車體發生二次碰撞而受傷害的可能性并沒有增大.初始設計和優化后車身與地面碰撞時的撞擊力曲線，如圖11所示.由圖11可知：優化后碰撞力峰值比初始模型降低16.9%，從而大大降低二次碰撞時對乘員的傷害.

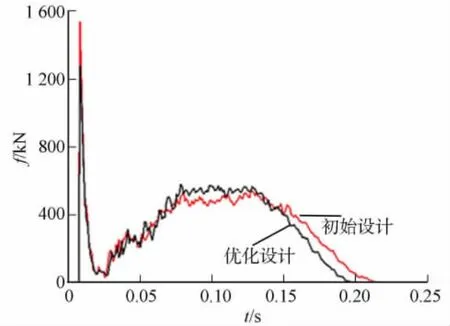
圖11 優化前后碰撞力曲線對比Fig.11 Comparison of the collision force before and after optimization

5 結論

根據客車側翻過程中立柱不同位置受力不同的特點，提出了一種新型梯度強度立柱結構，把每根立柱強度沿高度方向均勻分為6個單元，使得立柱不同位置強度與受力匹配.

結合最優拉丁方實驗設計采樣與RBF 近似技術，對立柱結構的強度與厚度進行了多目標最優匹配.優化結果表明：1）梯度強度立柱結構能明顯提高客車側翻安全性能；2）針對客車側翻優化問題，采用RBF徑向基近似模型有較高的精度，并大幅提高了優化效率；3）梯度強度立柱結構實現立柱結構減質量10.4%，達到了輕量化的目的；4）結合RBF 模型和NSGA－Ⅱ算法應用于客車側翻的多目標優化中，得出了Pareto最優解集，可以為設計人員提供多套設計方案參考.

［1］蘇鑾，李高波，呂光輝.長途客車交通事故原因及實例分析［J］.交通企業管理，2013（8）：71－72.

［2］中國公路車輛有限公司，金龍聯合汽車工業有限公司.GB 7578－2013客車上部結構強度要求及試驗方法［S］.北京：中國標準出版社，2014：13－18

［3］楊瑞峰，樊江順，崔海濤，等.基于ECE R66法規的某大客車上部結構強度［J］.公路交通科技，2011，28（10）：136－140.

［4］SU Rui－yi，GUI Lian－gjin，FAN Zi－jie.Multi－objective optimization for bus body with strength and roller safety constraints based on surrogate models［J］.Structural and Multidisciplinary Optimization，2011，44（3）：431－441.

［5］LIANG C C，LE G N.Optimization of bus rollover strength by consideration of the energy absorption ability［J］.International Journal of Automotive Technology，2010，11（2）：173－185.

［6］高云凱，張朋，吳錦妍，等.基于Kriging模型的大客車側翻安全性多目標優化［J］.同濟大學學報：自然自然版，2012，40（12）：1882－1887.

［7］胡泊，客車側翻安全性仿真研究及試驗驗證［D］.西安：長安大學，2012：55－58.

［8］馬曉光，王秋林，那景新，等.客車側翻結構安全性仿真分析及改進設計［J］.客車技術與研究，2011，41（8）：31－33.

［9］高云凱，高大威，余海燕，等.汽車用高強度鋼熱成型技術［J］.汽車技術，2010（8）：56－60.

［10］林建平，王立影，田浩彬，等.超高強度鋼板熱沖壓成形研究與發展［J］.熱加工工藝，2008，37（21）：140－144.

［11］ZHANG Yong，SUN Guang－yong，LI Guang－yao.Optimization of foam－filled bitubal structures for crashworthiness criteria［J］.Materials and Design，2012，38：99－109.

［12］關志華，寇紀淞，李敏強.一種改進的非支配排序遺傳算法INSGA［J］.天津大學學報：自然科學版，2002，35（4）：429－434.

［13］范子杰，馬林，桂良進，等.大客車側翻安全性多目標優化［J］.系統仿真學報，2012，24（5）：1109－1113.

［14］李恩穎，近似模型優化體系關鍵技術研究及應用［D］.長沙：湖南大學，2009：2－8.

［15］LIEFVENDAHL M，STOCKI R.A study on algorithms for optimization of latin hypercubes［J］.Journal of Statistical Planning and Inference，2006，136（9）：3231－3247.

［16］陳國棟.基于代理模型的多目標優化方法及其在車身設計中的應用［D］.長沙：湖南大學，2012：12－18

［17］廖興濤，張維剛，李青，等.響應表面法在薄壁構件耐撞性優化設計中的應用［J］.研究工程設計學報，2006，13（5）：298－302.