新的遞推有界GM 回歸估計算法

成立花，張俊敏

（1.西安工程大學(xué) 理學(xué)院，陜西 西安710048；2.西安建筑科技大學(xué) 理學(xué)院，陜西 西安710055）

最小二乘法（LS）和遞推的最小二乘法（RLS）是系統(tǒng)辨識中重要的算法.然而，在實際應(yīng)用中，由于各種干擾因素的存在，辨識所需的數(shù)據(jù)往往會被污染，包含數(shù)量和類型均未知的異常點.這些異常點使估計精度降低，甚至完全失效.解決這一問題通常有兩種方式：從數(shù)據(jù)中找出異常點并剔除掉，用剩余的數(shù)據(jù)進(jìn)行辨識；發(fā)展替代LS和RLS的魯棒回歸算法.由于后者簡便實用，備受學(xué)者關(guān)注，已發(fā)展出了許多算法［1－9］.在自回歸模型的參數(shù)估計中，數(shù)據(jù)中的異常點通常被分為兩個基本類［10］：加性異常點（第一型的異常點）與革新異常點（第二型的異常點）.革新異常點在系統(tǒng)運行過程中遵循了真實系統(tǒng)的關(guān)系，因此，就系統(tǒng)的辨識而言，其不利影響較小.然而，當(dāng)數(shù)據(jù)中包含較大量的加性異常點型杠桿點時，這些算法的估計性能會嚴(yán)重下降，甚至失效.針對廣義極大似然類（GM）估計器中存在的問題，本文提出新的遞推有界GM 回歸估計算法.

1 問題描述

考慮模型yi＝xiβ＋vi，i＝1，2，…，n.其中：β＝［b1，b2，…，bp］T；yi是第i時刻響應(yīng)變量觀測值；x＝［xi，1，xi，2，…，xi，p］；vi是相互獨立，且尺度參數(shù)σ未知的干擾項.所用的數(shù)據(jù)記作（Xn，Yn）.其中：Xn＝［xT2，xT2，…，xTn］T，Y＝［y1，y2，…，yn］T.獲得第n時刻的參數(shù)估計后，第i時刻相應(yīng)的殘差記作rn，i＝y(tǒng)i－.而在迭代法中，相應(yīng)于起始估計在第i時刻的殘差記作

采用文獻(xiàn)［9］中的一般框架，并加以改進(jìn)的風(fēng)險函數(shù)為

式（1）中：λ為遺忘因子，0＜λ≤1；d（xi），ξ（xi）為待定函數(shù)；ρ（·）是一個改進(jìn)于Huber函數(shù)的有界M－估計函數(shù)，即

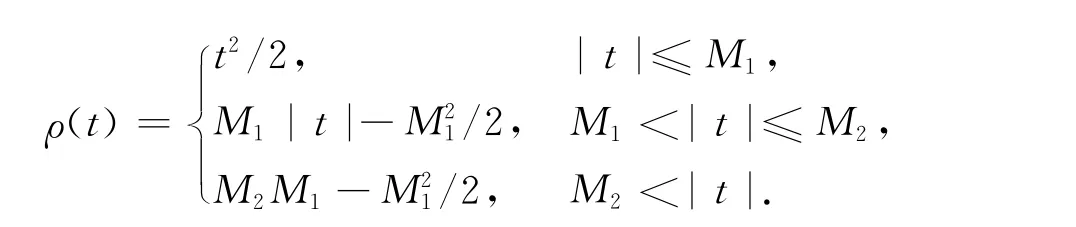
上式中：M為常值參數(shù).新估計器是式（1）的解.

2 新的GM 估計器

相應(yīng)于式（1）的“正規(guī)方程”為

式（2）中：ψ＝ρ′.

定義權(quán)函數(shù)為

上式中：sign（·）是符號函數(shù).因此，式（2）可寫為

用矩陣形式描述，有

式（4）中：Λn＝diag（λn－1，λn－2，…，λn－i，…，1）；Wn＝diag（w1，w2，…，wi，…，wn），wi＝

定義

由式（4）可得

式（5），（6）是新算法的基礎(chǔ)公式.

為確定d（xi）和ξ（xi）的具體形式，定義3個矩陣，有

上式中：（Wn）1／2＝一般地，這3個矩陣具有如下4個性質(zhì)：1）是對稱，但非冪等的；2）是冪等，但非對稱的；3）HWn是冪等對稱的，且其對角元素hwi的范圍為的對角元素的范圍為0≤≤1.

引理［11］設(shè)XTnXn可逆，則矩陣Hn＝Xn（XTnXn）－1XTn為冪等對稱矩陣，且其對角元素hi的范圍為0≤hi≤1.矩陣Hn的對角元素通常被用來檢測杠桿點.

證明 性質(zhì)1），2）的結(jié)論很容易得到，所以只需證明性質(zhì)3）即可.

假設(shè)ˉWn是Wn中非零的相應(yīng)部分，，分別是Λn，Xn中相應(yīng)于的部分，且類似于普通最小二乘法中XTnXn是可逆的假設(shè).新估計器中假定是可逆的，式（5）可簡化為WPn＝.而，的乘積是非奇異的，令在HWn中相應(yīng)于ˉWn的部分可以表示為

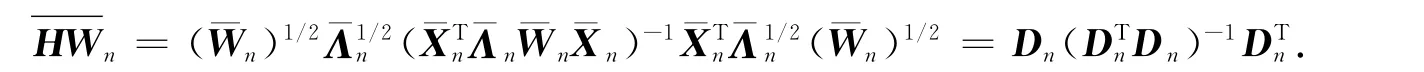
根據(jù)性質(zhì)1），HWn是冪等對稱的，且其對角元素的范圍為0≤≤1.又因為HWn中相應(yīng)于權(quán)重為0的對角元素也是0，所以對于HWn的所有對角元素，有0≤hwj≤1.

下面分析基于式（5），（6）的殘差特性.

定理 殘差rn，i的方差（σ（i）λ）2與之間滿足

證明 根據(jù)式（6），殘差向量的形式有

式（7）中：In為n階單位矩陣.

在觀測噪聲為獨立同分布的假設(shè)之下，殘差向量rn的協(xié)方差矩陣為

于是殘差rn，i的方差為

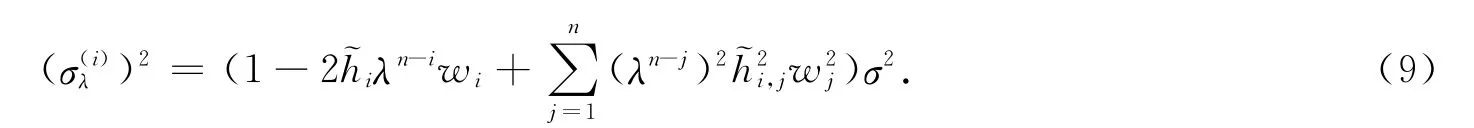
式（9）中：是的第i行第j列的元素；表示其對角線上的相應(yīng)元素.注意到（λn－j）≤λn－j，j＝1，2，…，n，且0≤wj≤1，易得

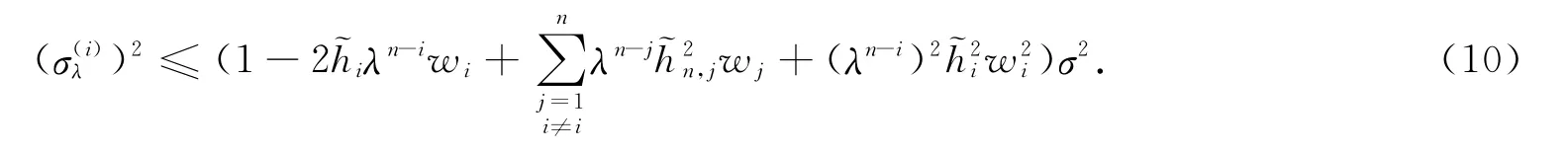
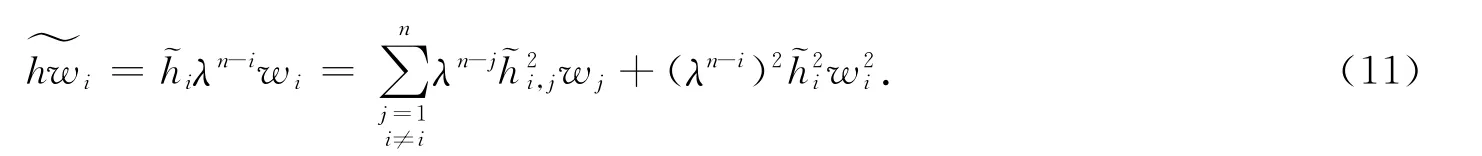
因而，把式（11）代入式（10），可得

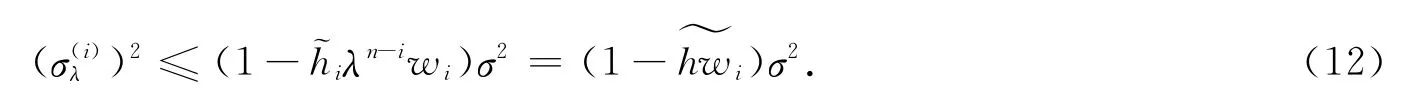
由性質(zhì)4），又因為式（12）右邊是非負(fù)的，考慮到在權(quán)重矩陣和遺忘因子確定的情況下是關(guān)于xi的函數(shù)，取并定義一個統(tǒng)計量考慮到Hn的對角元素hi是的特殊形式，且對普通的最小二乘法而言，hi有檢測回歸變量中異常點的功能.為了避免的值接近1時，造成計算上的誤差，定義ξ（·）函數(shù)為

上式中：K為可調(diào)的參數(shù).該參數(shù)確定數(shù)據(jù)xi是否為異常點.如果＜K，認(rèn)為xi是正常的；否則，認(rèn)為xi是異常的.為方便，將ξ（xi），d（xi）分別記作

新遞推估計器采用一步迭代法推導(dǎo).假定在n－1時刻的權(quán)矩陣Wn－1和相關(guān)的估計，Pn－1已經(jīng)得到，那么相應(yīng)的式（5），（6）可以表示為

我八歲的時候，我父親就去世了，我母親一個人帶大我們哥倆。我們在內(nèi)蒙古偏遠(yuǎn)的地方帶大，我在北京沒有一個親戚，我沒有因為自己的工作送過一回禮，我不也走到了今天嗎？我知道社會上有很多不良的現(xiàn)象，我告訴你，信那些該信的東西，因為它能改變你。因為如果你要信那些你沒法不憤怒的事情，它只能害了你。

此時，初始權(quán)重矩陣取W（0）n＝diag（diag（Wn－1），1），而，Pn的初始估計為

式（15），（16）中：P（－0）n為P（0）n的逆矩陣.

令A(yù)＝，C＝Ip，B＝DT＝xTn，并將矩陣的逆的公式（A＋BCD）－1＝A－1－A－1B（DA－1B＋C－1）－1DA－1應(yīng)用于式（15），則的遞推計算公式變?yōu)?/p>

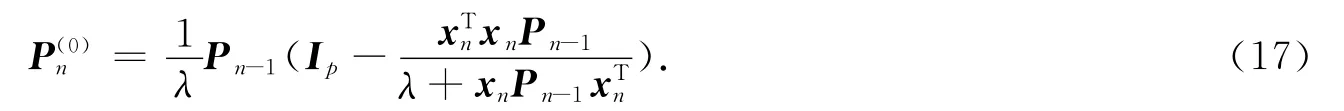
迭代開始后，需要計算再加權(quán)矩陣.此時，只對wn進(jìn)行更新，保持W（0）n中的相應(yīng)元素不變，即取＝diag（diag（Wn－1），wn）.由于λ0＝1，＝1，易知因此，.一個更好的做法是將W（0）n的對角元素都進(jìn)行更新.然而，為了得到遞推的計算公式，這種做法不得不放棄.但是，引入的遺忘因子和所用M－估計函數(shù)的有界性可以降低這種影響.

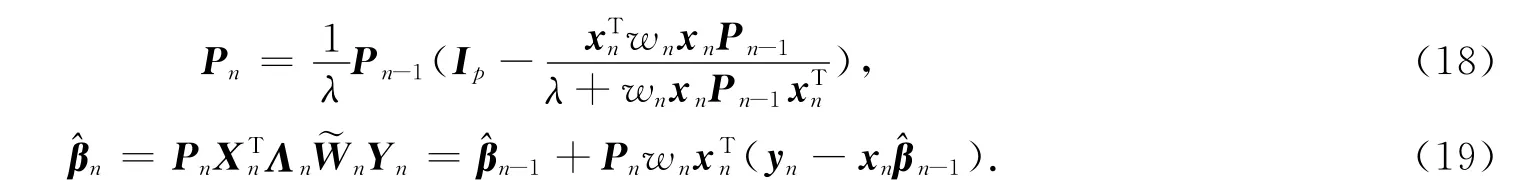
式（16）～（19）形成了遞推有界廣義極大似然類（RBGM）回歸估計器.為了降低計算量，新估計器還可以描述為

輸入：，Pn－1，（xn，yn）；

輸出：，Pn；

3 AR 模型參數(shù)估計算法

在觀測數(shù)據(jù)中含有較大量加性異常點的情況下進(jìn)行AR 模型參數(shù)估計時，RBGM 也是有偏的.為此，需要對其進(jìn)行必要的改造，把面向AR 模型參數(shù)估計的算法記作AR－RBGM.

首先，用，替換RBGM 中的xn，βn.＝［b1，b2，…，bp，η1］，＝［yn－1，yn－2，…，yn－p，εn－1］（η1為增廣參數(shù)，εn－1為增廣變量）.在初始化時，εn－1和η1 都賦0值.在運行期間，隨著算法自動更新.

其次，增加一個加性異常點的檢測過程.在此過程中涉及兩種殘差的計算，一是不包括增廣項的rn，n，二是包括增廣項的殘差＝y(tǒng)n－.在當(dāng)前n時刻的估計已經(jīng)得到后，假設(shè)以前的加性異常點的影響已經(jīng)體現(xiàn)在增廣項里，且當(dāng)前的觀測數(shù)據(jù)不是加性異常點，那么相應(yīng)的接受域為，而相應(yīng)的拒絕域為其中：γ是個可調(diào)常數(shù)，一般取1.5左右即可.據(jù)檢驗結(jié)果可知：如果拒絕了假設(shè)，則認(rèn)為yn是加性異常點，其影響應(yīng)該體現(xiàn)在增廣項中，相應(yīng)地取εn＝rn，n；否則，取εn＝0.此外，是用替換rn，j后，通過式（20）計算得到的，而在用RLS進(jìn)行啟動的階段，可直接用med估計，也可以借用先驗估計結(jié)果.

在AR 模型參數(shù)估計時，無論數(shù)據(jù)中包含或不包含異常點，異常點是革新或加性，AR－RBGM 中的參數(shù)都無須重置.另外，RBGM 和AR－RBGM 追蹤系統(tǒng)突變的能力主要依賴于遺忘因子的大小，當(dāng)需要追蹤突變時，遺忘因子相對取小一點，如0.99等；不需要追蹤突變時，遺忘因子則取得相對大一點，如0.999或0.999 9等.在估計精度和對突變的追蹤能力方面需要折中取舍.

4 仿真實驗

在實驗中，假定需要辨識的真實系統(tǒng)為

式（20）中：ei為相互獨立同分布的隨機(jī)變量，且ei～N（0，σ21）.該模型已經(jīng)在文獻(xiàn)［5，10］中被用來檢驗M 和GM 估計器的魯棒性.

在觀測值的仿真實驗中，如果第一型異常點出現(xiàn)，相應(yīng)的觀測值yi用yi＝zi＋vi進(jìn)行模擬.其中：vi～（1－κ1）ד0”＋κ1×N（0，σ22），如果第二型異常點出現(xiàn)，相應(yīng)的觀測值yi通過把式（21）中的ei替換為另一個隨機(jī)變量ni，并令yi＝zi進(jìn)行模擬.其中：ni～N（0，σ21）＋κ2×N（0，σ23）.在仿真實驗中，設(shè)計了4種更加復(fù)雜的情形，觀測數(shù)據(jù)如表1所示.每一種情形都將整個過程分成3個階段，并且假定第一型異常點或者第二型異常點分別出現(xiàn)在某一個階段.

在所有情形中，取σ21＝25，κ1＝0.05，κ2＝0.05，σ22＝σ23＝400.采用對數(shù)化平均相對誤差（LMRE）來刻畫估計精度及收斂性，即

式（21）中：M為程序運行的次數(shù)；β為系統(tǒng)的真實參數(shù)；為在第m次運行時，n時刻β的估計.

表1 4種情形的觀測數(shù)據(jù)Tab.1 Four types of observed data

實驗中用經(jīng)典的RLS和另外兩種遞推的GM 估計器RGM［8］和RKW［4］做了比較.在沒有異常點的情況下這幾種估計器的表現(xiàn)，如圖1所示.圖1 中：LMRE 為對數(shù)化平均相對誤差；n為時序.在比較時，每種估計器都進(jìn)行了參數(shù)調(diào)整以使其表現(xiàn)盡可能達(dá)到最好.具體地，對RLS，λ＝0.999 9；對RGM，λ＝0.999 9，c＝2.8，P（0）＝100I2；對RKW，P（0）＝A－1（0）＝100I2，λ＝0.999 9，c＝2，a＝5；對RBGM 和AR－RBGM，λ＝0.999 9，NInitial＝10，λσ＝0.98，γ＝1.5，L＝20，K＝0.85，M1＝1.88，M2＝2.41.為了方便比較，所有的初始尺度估計中，σ0＝5.實驗結(jié)果表明：在此情形下，除了AR－RBGM 的表現(xiàn)稍差以外，其他估計器表現(xiàn)相當(dāng).因為AR－RBGM 中的增廣項改變了原始模型的結(jié)構(gòu)，對其性能產(chǎn)生了有限的影響.

非平穩(wěn)環(huán)境（情形2～4）下估計性能比較，如圖2～4所示.圖2～4中：LMRE為對數(shù)化平均相對誤差；n為時序.由圖2，3可知：即使當(dāng)加性異常點出現(xiàn)在算法已達(dá)到或者接近穩(wěn)定狀態(tài)時，RLS，RGM，RKW 完全失效，而RBGM 對這些影響抑制效果是明顯的，但精度仍然不高；AR－RBGM 能在各種情形下都保持較高的精度和收斂性，其精度與沒有異常點時的精度差別很小.由圖4可知：對加性異常點出現(xiàn)在初始階段的情形，仍然是AR－RBGM 保持較高精度和良好收斂性，其他估計器全部失；加性異常點出現(xiàn)在起始階段時，AR－RBGM 的相應(yīng)的指標(biāo)會變大一點，這主要是受到非魯棒啟動算法RLS的影響.

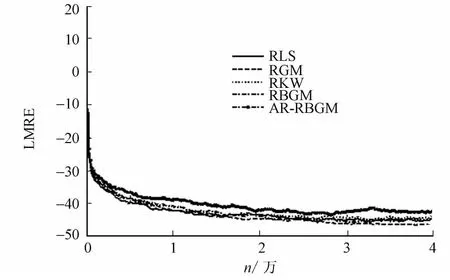
圖1 平穩(wěn)環(huán)境（情形1）下估計性能比較Fig.1 Performance comparison of the algorithm for the stability environment（case 1）

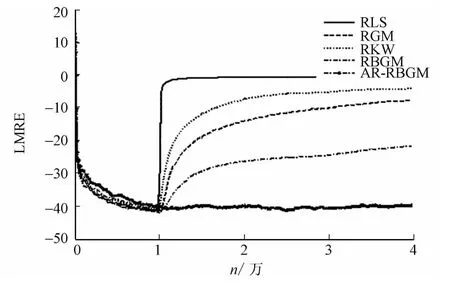
圖2 非平穩(wěn)環(huán)境（情形2）下估計性能比較Fig.2 Performance comparison of the algorithm for the unstability environment（case 2）

圖3 非平穩(wěn)環(huán)境（情形3）下估計性能比較Fig.3 Performance comparison of the algorithm for the unstability environment（case 3）

圖4 非平穩(wěn)環(huán)境（情形4）下估計性能比較Fig.4 Performance comparison of the algorithm for the unstability environment（case 4）

5 結(jié)束語

改進(jìn)GM 估計器的一般框架，提出一種新的遞推GM 回歸估計器（RBGM），并針對AR 模型參數(shù)估計提出了AR－RBGM.RBGM 和AR－RBGM 均能對回歸變量中的加性異常點的影響起到抑制作用，特別是AR－RBGM 能在非平穩(wěn)環(huán)境下實現(xiàn)自適應(yīng)的估計，并保持良好的精度和收斂性.新估計器還可以進(jìn)行改進(jìn)，一方面，魯棒的啟動算法可以提高性能；另一方面，可進(jìn)一步推廣到ARMA 模型參數(shù)的估計中，從而獲得相應(yīng)的魯棒算法.然而，由于AR－RBGM 引入了增廣變量，增加了額外的計算量.

［1］HUBER P J.Robust regression：Asymptotics，conjectures and monte carlo［J］.Annals of Statistics，1973，1（5）：799－821.

［2］CAMPBEL K.Recursive computation of M－estimates for the parameters of a finite autoregressive process［J］.The Annals of Stat，1982，10（2）：442－453.

［3］ANTOCH J，EKBLOM H.Recursive robust regression computational aspects and comparison［J］.Computational Statistics and Data Analysis，1995，19（2）：115－128.

［4］SEJLING K，et al.Methods for recursive robust estimation of AR parameters［J］.Computational Atatistics and Data Analysis，1994，17（5）：509－536.

［5］PHAM D S，ZOUBIR A M.A sequential algorithm for robust parameter estimation［J］.IEEE Signal Processing Lett，2005，12（1）：21－24.

［6］VEGA L R，REY H，BENESTY J，et al.A robust recursive least squares algorithm［J］.IEEE Trans Signal Process，2009，57（3）：1209－1216.

［7］KRASKER W S，WELSCH R E.Efficient bounded－influence regression estimation［J］.Journal of the American Statistical Association，1982，77（379）：595－604.

［8］GRILLENZONI C.Recursive generalized M－estimators of system parameters［J］.Technometrics，1997，39（2）：211－224.

［9］ENGIUND J E.Recursive versions of the algorithm by Krasker and Welsch［J］.Sequential Analysis，1991，10（3／4）：211－234.

［10］MARONNA R A，MARTIN R D，YOHAI V J.Robust statistics：Theory and methods［M］.West Sussex：John Wiley＆Sons，2006：888－889.

［11］ROUSSEEUW P J，LEROY A M.Robust regression and outlier detection［M］.New York：Wiley，1987：340－347.