局部放電UHF 脈沖的時頻特征提取與聚類分析

汪 可 廖瑞金 王季宇 楊麗君 李 劍

（1.中國電力科學(xué)研究院 北京 100192 2.重慶大學(xué)輸配電裝備及系統(tǒng)安全與新技術(shù)國家重點(diǎn)實(shí)驗(yàn)室 重慶 400044）

1 引言

隨著電網(wǎng)電壓等級的逐步提高和輸電容量的不斷增大，對特高壓輸變電裝備的絕緣可靠性也提出了更嚴(yán)格的要求。局部放電（Partial Discharge,PD）被認(rèn)為是導(dǎo)致電氣設(shè)備故障的重要原因之一[1-3]，采集并分析局部放電信號，對于診斷特高壓電氣設(shè)備的絕緣狀態(tài)具有重要意義。

國內(nèi)外對電氣設(shè)備內(nèi)部局部放電缺陷類型的診斷和識別進(jìn)行了大量的研究工作[4-6]，重點(diǎn)是通過實(shí)驗(yàn)室構(gòu)造人工缺陷模型并采集信號，提取特征構(gòu)造訓(xùn)練指紋庫，設(shè)計(jì)合理的智能分類器對局部放電類型進(jìn)行識別和診斷。然而，電氣設(shè)備在制造、運(yùn)輸過程中產(chǎn)生的氣泡、尖端等潛伏性缺陷，在長期運(yùn)行電壓作用下，往往在多處引發(fā)局部放電，測量到的局部放電往往是多處放電源信號的疊加，導(dǎo)致傳統(tǒng)的單一缺陷指紋庫無法應(yīng)用于診斷多局部放電源。因此，在多個放電源同時存在時，對局部放電缺陷的診斷可以分為兩個部分：脈沖分離與分類識別。其中，脈沖分離是識別多放電源的核心所在，屬于無監(jiān)督聚類問題，即通過提取某種具有代表性的特征使得具有類似特征的脈沖能夠自動地聚集成一類，從而實(shí)現(xiàn)脈沖的有效分離。因此，提取可靠的脈沖特征從而有效反映不同放電源之間的差異，是實(shí)現(xiàn)脈沖自動分離的關(guān)鍵性問題。目前已提出的方法有等效時頻分析[7]、自相關(guān)函數(shù)法[8]、小波分解結(jié)合主成分分析法[9]、包絡(luò)線比較[10]以及盲源分離[11]等。

在眾多局部放電監(jiān)測手段中，超高頻（Ultra High Frequency,UHF）天線因其高靈敏度和超寬頻帶等優(yōu)點(diǎn)逐漸成為研究的熱點(diǎn)[12]。文獻(xiàn)[13]指出局部放電UHF 脈沖持續(xù)時間為納秒級，在這個時間內(nèi)同時發(fā)生兩次或更多的放電幾乎不可能。因此，采集PD 的UHF 脈沖信號并進(jìn)行自動聚類即可對放電源信息進(jìn)行診斷。研究表明局部放電的UHF 脈沖是典型的非平穩(wěn)信號[14]，單純地從時域或頻域提取的特征并不能完整地反映局部放電的全部信息，而時頻聯(lián)合分析則是有效的解決辦法。S 變換（S Transform,ST）是由地球物理學(xué)家Stockwell 于1996年提出的一種時頻分析方法[15]，其時窗寬度與頻率呈逆向變化，使得ST 在低頻段能夠取得較高的頻率分辨率，而在高頻段可以獲得較高的時間分辨率，因而集成了短時傅里葉變換（Short Time Fourier Transform,STFT）和連續(xù)小波分析（Continuous Wavelet Transform,CWT）的優(yōu)點(diǎn)。并且，ST 還具有計(jì)算效率高的優(yōu)勢，更有利于非平穩(wěn)信號的在線分析與處理。文獻(xiàn)[16]首次引入ST 對局部放電脈沖信號進(jìn)行時頻分析，并用于提取及分辨淹沒在現(xiàn)場噪聲干擾中的局部放電脈沖信號。然而，對于局部放電脈沖的ST 時頻特征提取問題卻鮮見文獻(xiàn)報(bào)道。

本文重點(diǎn)探索基于ST 的局部放電UHF 脈沖時頻特征提取與診斷策略。首先，采用ST 對局部放電UHF 脈沖的時頻特性進(jìn)行表征，采用非負(fù)矩陣分解（Non-negative Matrix Factorization,NMF）方法對ST 時頻矩陣進(jìn)行分解得到一系列頻域基向量與對應(yīng)的時域位置向量。然后，對每個頻域基向量和時域位置向量提取了尖銳度、導(dǎo)數(shù)平方和、信息熵以及稀疏度等參量，構(gòu)造出能充分反映局部放電脈沖時頻信息的特征空間，最后引入模糊C 均值（Fuzzy C-Means,FCM）聚類算法對提取的特征進(jìn)行脈沖聚類分析，并利用實(shí)驗(yàn)室采集的4 種缺陷類型的局部放電UHF 脈沖對該方法的有效性進(jìn)行了校驗(yàn)，并與常用的局部放電時頻分析方法Wigner-Ville 分布（WVD）進(jìn)行了對比。

2 基于ST 的脈沖時域→時頻域映射

信號x(t)的ST 定義如下[15]

式中，h(t-τ,f)為高斯窗口；τ為控制高斯窗口在時間軸t 上的位置參數(shù)；f 表征頻率；j為虛數(shù)單位。

h(t-τ,f)的表達(dá)式如式（2）所示

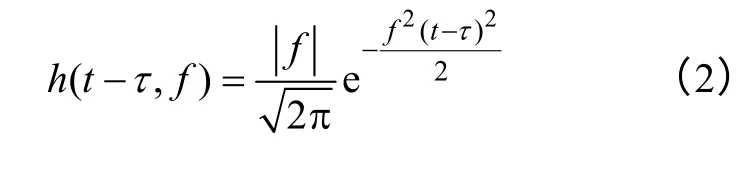
將式（2）代入式（1），ST 的表達(dá)式可以轉(zhuǎn)化為

本文采用S 變換幅值（S Transform Amplitude,STA）矩陣來表征局部放電UHF 脈沖的時頻信息，該矩陣的列為時間采樣點(diǎn)，行為對應(yīng)的頻率采樣點(diǎn)。

3 特征提取

3.1 非負(fù)矩陣分解

NMF 可以表示為：給定一個待分解的非負(fù)矩陣VN×M，求非負(fù)的矩陣WN×r和Hr×M使得

式中，WN×r為基向量矩陣，Hr×M為系數(shù)矩陣。WN×r和Hr×M可以表示為一維向量的組合

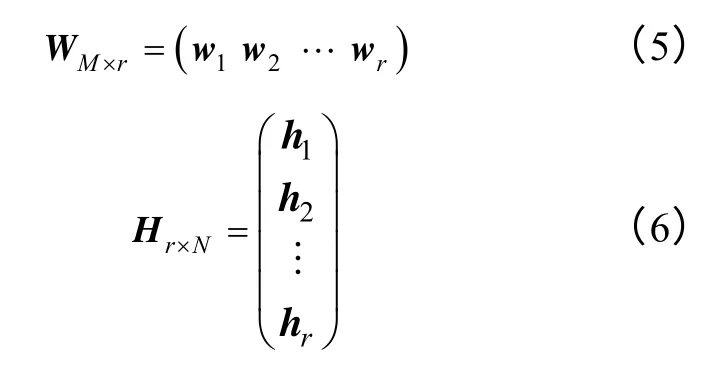
因此，V 矩陣是W 矩陣列向量{wi}i=1,…,r的線性組合，系數(shù)即為H 矩陣的行向量{hi}i=1,…,r。通常，參數(shù)r 滿足(n+m)r＜nm，即可實(shí)現(xiàn)數(shù)據(jù)壓縮。在實(shí)際求解W 和H 矩陣時，首先對W 和H 進(jìn)行初始化，設(shè)置一定的目標(biāo)函數(shù)反映V 矩陣與WH 矩陣之間的差異，采用迭代的方法使目標(biāo)函數(shù)達(dá)到最小。本文參照文獻(xiàn)[17]，采用基于Kullback-Leibler（KL）散度的目標(biāo)函數(shù)fcost，如式（7），并采用乘法迭代規(guī)則（Multiplicative Update Rule,MUR）[17]不斷更新W 和H 矩陣的元素，迭代規(guī)則如式（8）～式（9）。

通過式（8）和式（9）的反復(fù)迭代，當(dāng)達(dá)到設(shè)置的迭代次數(shù)時，即可得到基向量矩陣W 及其系數(shù)矩陣H。

3.2 特征提取

NMF 將STA 矩陣分解為基矩陣W=(w1w2,…,wr)以及系數(shù)矩陣H=(h1h2,…,hr)T，其中，{wi}i=1,…,r和{hi}i=1,…,r為頻域基向量及對應(yīng)的時域位置向量，包含了PD 脈沖原始時頻矩陣的絕大部分信息。本文從{wi}i=1,…,r和{hi}i=1,…,r中提取以下特征參量。

3.2.1 尖銳度SH

尖銳度（Sharpness）能夠反應(yīng)信號的頻域能量信息。對于每一個頻域基向量{wi}i=1,…,r，首先對其進(jìn)行傅里葉變換（Fourier Transform,FT），如式（10）。

式中，Wi(v)是基向量wi的傅里葉變換結(jié)果。

然后，對Wi(v)進(jìn)行如式（11）所示的變換得到Wi(k)，最后將Wi(k)中從n0到N/4 項(xiàng)的元素絕對值求和即可得到尖銳度SHwi，如式（12）。式中，n0為小于N/4 的一個較小的正整數(shù)，本文取n0=10。

導(dǎo)數(shù)平方和（sum of derivative）能夠直觀地對向量中元素的均勻性進(jìn)行度量。頻域基向量{wi}i=1,…,r的導(dǎo)數(shù)平方和SD 定義如式（13）所示。

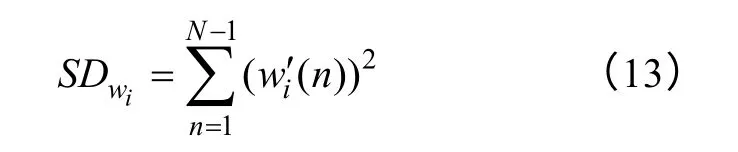
3.2.3 信息熵EN

信息熵（Entropy）由Shannon 提出，可以反映序列的平均信息量，分別采用式（15）和式（16）計(jì)算頻域基向量{wi}i=1,…,r和時域位置向量{hi}i=1,…,r的信息熵EN。

3.2.4 稀疏度SP

稀疏度（Sparsity）主要反映元素之間偏移量，采用式（17）對{hi}i=1,…,r計(jì)算稀疏度SP。

式中，M為hi的長度。

上述三種信號只要一項(xiàng)達(dá)到危險(xiǎn)條件就啟動報(bào)警模塊。方案一采用2輸入四或門的7432或門芯片，三個信號接1、2、5口，輸出3與4連，輸出6接負(fù)載。方案二采用STC89C52單片機(jī)，當(dāng)熱釋電紅外傳感器有信號、金屬接近傳感器無信號、DHT11溫濕度傳感器溫度達(dá)到50℃三種情況有一項(xiàng)達(dá)到報(bào)警指標(biāo)，即P1.1收到高電平信號，P1.2收到低電平信號，P1.3大于50℃信號，P1.4輸出信號高電平，蜂鳴器鳴叫或觸發(fā)繼電器，達(dá)到報(bào)警效果。

由式（17）可知，當(dāng)向量中所有元素相等時，其稀疏度SP=1。

綜上所述，從每個wi提取了（SHwi,SDwi,ENwi）三個特征參量，而每個hi提取了（ENhi,SPhi）兩個特征參量。因此，隨著r 取值的不同，從局部放電脈沖的STA 矩陣中提取的特征集Features 可以表示為式（18），特征維數(shù)為5×r。

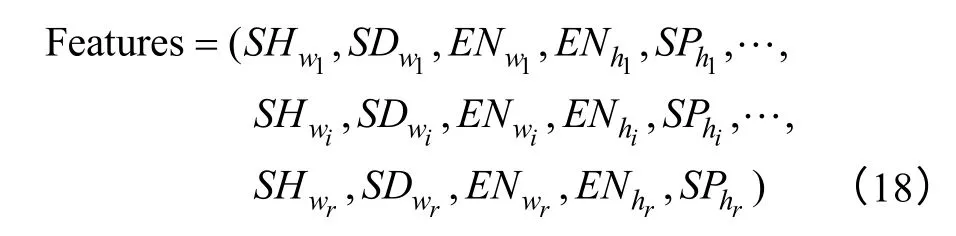
4 FCM 聚類

FCM 是一種基于目標(biāo)函數(shù)的聚類算法，采用樣本到聚類中心的距離平方和作為目標(biāo)函數(shù)，將聚類歸結(jié)為一個帶約束的非線性規(guī)劃問題。對于給定的脈沖特征樣本集F={f1,f2,…,fN}，其中fi=(fi1,fi2,…,fim)T，F(xiàn)CM 算法的數(shù)學(xué)表述如下：

式中，c為聚類數(shù)；μij為樣本j 屬于第i 類的隸屬度；vi為第i 類中心；m為權(quán)重指數(shù)，取值范圍一般為1.5～2.5，本文取m=2。‖fj-vi‖2表征樣本j 到第i類中心的歐式距離。FCM 的詳細(xì)算法流程詳見文獻(xiàn)[18]，本文不予重述。

劃分系數(shù)（Partition Coefficient,PC）和分類熵（Classification Entropy,CE）是衡量FCM 聚類效果最常用的兩個參量，其表達(dá)式分別如式（21）和式（22）。PC 值越大，CE 值越小，表明聚類效果越好。

5 局部放電試驗(yàn)

設(shè)計(jì)了四種典型的局部放電人工缺陷模型：絕緣內(nèi)部氣隙放電、油中沿面放電、油中懸浮電極放電以及油中電暈放電，分別記為P1～P4。各類放電模型如圖1 所示。

圖1 局部放電人工缺陷模型1—球電極 2—圓板電極 3，9—環(huán)氧板 4—?dú)庀?—有機(jī)玻璃板 6—絕緣螺帽 7—絕緣螺栓8—圓柱電極 10—金屬顆粒 11—針電極Fig.1 Artificial defect models of PD

圖1a為模擬固體絕緣內(nèi)部局部放電的電極系統(tǒng)及缺陷模型結(jié)構(gòu)，采用絕緣薄膜在板電極表面支撐環(huán)氧板形成厚度為0.15 mm，直徑為38 mm 的氣隙。試驗(yàn)中將整個模型浸入絕緣油以防止氣隙外部發(fā)生放電。圖1b 和1c 是模擬油中沿面放電和油中懸浮電極放電的電極系統(tǒng)結(jié)構(gòu)，試驗(yàn)?zāi)Ｐ途恢萌虢^緣油中模擬油中放電，其中，懸浮電極模型中的環(huán)氧板邊緣放置有直徑為0.3mm 的金屬球。圖1d為針–板電極系統(tǒng)，電極系統(tǒng)浸入絕緣油中模擬油中放電時，針尖到環(huán)氧板之間的距離為1mm。試驗(yàn)電路詳見文獻(xiàn)[19]，人工缺陷模型和絕緣油放置在有機(jī)玻璃試驗(yàn)容器中。

UHF 傳感器采用四階分形天線，該傳感器的3 個諧振頻率約為261MHz、516MHz 和869MHz，當(dāng)駐波比小于5 時，每個諧振頻率的通頻帶大約為150～320MHz，430～620MHz 和740～1 000MHz。試驗(yàn)中，UHF 天線與試驗(yàn)容器的距離約為15cm，采集數(shù)據(jù)的電壓為起始放電電壓的1.3～1.8 倍，對于每種局部放電類型，在3 個電壓下進(jìn)行數(shù)據(jù)采集，每個電壓下采集了50 組放電樣本，共50×3×4=600組樣本，采樣率為5GS/s。

6 分析與討論

6.1 數(shù)據(jù)預(yù)處理

由于局部放電的隨機(jī)性，放電脈沖的幅值和寬度都存在一定的分散性，幅值分布在幾百毫伏到幾伏的范圍內(nèi)，通常持續(xù)幾百納秒。本文首先對采集的信號進(jìn)行歸一化預(yù)處理去除幅值分散性。同時，為了消除持續(xù)時間分散性對特征提取的影響，采集了1 000ns 的局部放電信號得到完整的局部放電UHF 波形。對采集的UHF 信號進(jìn)行進(jìn)一步統(tǒng)計(jì)分析發(fā)現(xiàn)，所有的信號均可以用1 000 個數(shù)據(jù)點(diǎn)進(jìn)行表征，如圖2 所示。本文選取的是數(shù)據(jù)點(diǎn)2 451～3 450 之間的信號。經(jīng)過預(yù)處理后的四種典型局部放電UHF 信號如圖3 所示，每個脈沖波形包括1 000個數(shù)據(jù)點(diǎn)。

圖2 典型的局部放電UHF 信號Fig.2 Typical UHF signals of PD

圖3 典型的局部放電UHF 信號Fig.3 Typical UHF signals of PD

6.2 時頻分析及特征提取

圖3 中四種典型的局部放電UHF 信號的S 變換結(jié)果如圖4 所示，每個STA 矩陣的維數(shù)為500×1 000。從圖4 中可以直觀地看出，不同放電源脈沖信號的STA 矩陣具有相互區(qū)別的時頻特征。對每個STA 矩陣進(jìn)行NMF 運(yùn)算得到一系列頻域基向量{wi}i=1,…,r和時域位置向量{hi}i=1,…,r，并進(jìn)一步提取得到如式（18）的特征集。圖5 和圖6 給出了r=1 時4 類放電的5 個局部放電特征值。本文在進(jìn)行FCM 聚類之前對提取的特征參量進(jìn)行歸一化處理，消除特征量數(shù)量級的影響。

圖4 典型的局部放電UHF 信號的S 變換Fig.4 S transform of typical UHF signals of PD

圖5 r=1 時提取的SHw1，SDw1，SPh1Fig.5 The extracted SHw1，SDw1，SPh1with r=1

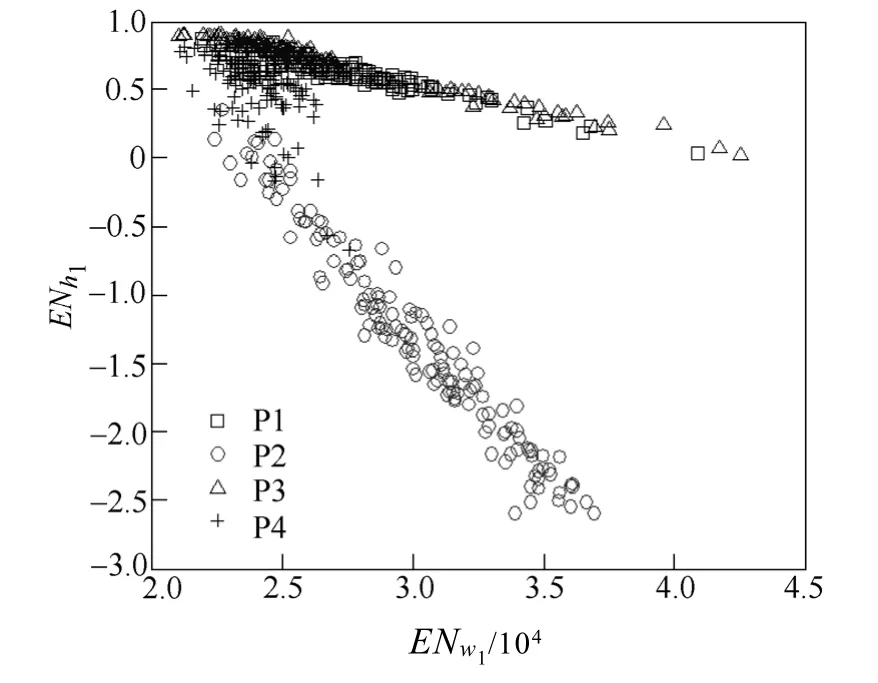
圖6 r=1 時提取的ENw1，ENh1Fig.6 The extracted ENw1，ENh1with r=1

6.3 FCM 聚類結(jié)果分析

圖7 給出了當(dāng)r 取1 到5 時FCM 對四類放電模型600 組樣本的聚類結(jié)果，其中縱坐標(biāo)表征的是P1～P4 的150 組樣本被劃分到每一類的樣本數(shù)。從圖7 中可以看出，當(dāng)r=1,2,3,5 時（提取的特征分別為5,10,15,25 維），P1～P4 的大部分樣本被依次劃分為第1、第4、第3 和第2 類，當(dāng)r=4 時，P1～P4 的大部分樣本被依次劃分為第4、第1、第3 和第2 類。因此，圖7 直觀地說明了提取的特征集對于脈沖聚類分離的有效性，并且不受試驗(yàn)電壓的影響。

圖7 4 類放電600 組樣本的FCM 聚類結(jié)果Fig.7 FCM clustering results of 600 samples of four PD types

對于P1～P4 每一類放電，通過統(tǒng)計(jì)FCM 聚類得到的類別矩陣中最大的樣本數(shù)，并除以總樣本數(shù)即可得到在不同特征集下局部放電脈沖的聚類正確率。圖8為隨著r 的增加FCM 的聚類正確率及聚類評價(jià)指標(biāo)PC 和CE 的變化圖譜。由圖可知，當(dāng)r=2時，對應(yīng)的10 維特征集能夠取得最高為90.33%的聚類正確率。當(dāng)r 從1 增加到5 時，聚類正確率先增加后逐漸減小，呈“倒V”形變化規(guī)律。同時，聚類指標(biāo)PC 和CE 也呈現(xiàn)同樣的變化規(guī)律，表明隨著r 的增加，F(xiàn)CM 的聚類效果也是先增強(qiáng)后減弱，在r=2 時最好。這是可能是由于，當(dāng)r=1 時，NMF僅僅分解得到一個頻域基向量和時域位置向量，丟失了一定的時頻信息，導(dǎo)致聚類正確率僅79.83%。隨著r 的逐步增加，分解的頻域基向量與時域位置向量變多，時頻信息逐漸被展開，每個頻域基向量和時域位置向量中包含的信息量減少。對于不同放電源產(chǎn)生的放電脈沖，提取的特征參量之間差異性逐漸減小，因此聚類的正確率逐漸降低。

圖8 FCM 聚類結(jié)果與NMF 參數(shù)r 的關(guān)系Fig.8 The development of FCM clustering results with NMF parameter r

圖9為將r=2 時提取的10 維特征參量映射到二維平面時的樣本散點(diǎn)圖，由圖9 中可以看出，P1～P4 的放電脈沖樣本較為清晰地聚成四類，證明了ST 時頻特征用于不同放電源脈沖聚類的有效性。

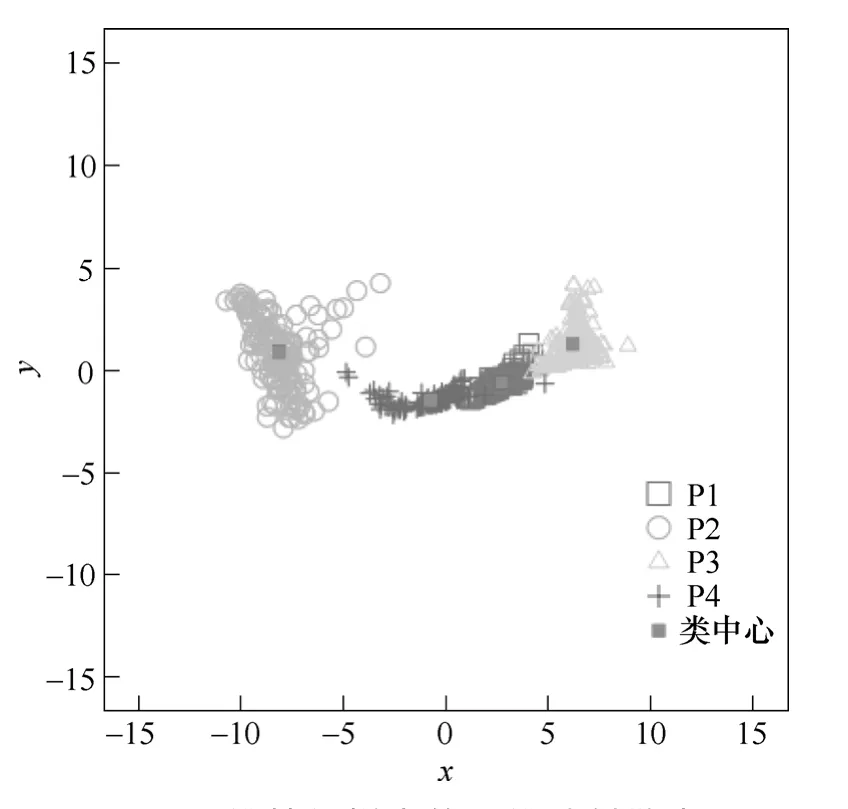
圖9 10 維特征樣本的二維映射散點(diǎn)圖Fig.9 Two dimensional scatter plot of the 10 dimensional feature vectors

6.4 ST 與WVD 的對比

Wigner-Ville 分布（WVD）是Cohen 類時頻分布中最具代表性的非平穩(wěn)信號時頻分析方法，被廣泛應(yīng)用于各類局部放電脈沖的時頻分析[20-22]。對于相同的局部放電UHF 脈沖樣本，本文也采用WVD進(jìn)行時頻分析，并提取了如式（18）的脈沖特征，其FCM 聚類結(jié)果如表1 所示。

表1 ST 與WVD 特征的局部放電脈沖聚類結(jié)果（%）Tab.1 Partial discharge pulses clustering results of ST and WVD based features

從表1 中可以看出，r 取值為1 到5 時，WVD的聚類正確率較ST 均有不同程度的降低，也在r=2 時取得最大聚類正確率86.83%。WVD 屬于雙線性時頻分布，存在一定的交叉項(xiàng)干擾，阻礙了局部放電UHF 脈沖時頻信息的準(zhǔn)確提取；另一方面，ST集成了STFT 和CWT 的優(yōu)點(diǎn)，能夠以高時頻分辨率挖掘足夠信息。從識別結(jié)果上看，ST 較傳統(tǒng)的WVD更適合進(jìn)行局部放電UHF 脈沖的分析。

6.5 不同信號傳播路徑對聚類結(jié)果的影響

為了模擬變壓器繞組和箱壁對UHF 脈沖的折反射作用，將人工缺陷模型放置于高度為75cm、直徑為90cm 的鋼質(zhì)油箱中，并在油箱內(nèi)放置一個人工模擬的變壓器小型繞組。油箱的兩側(cè)各有一個檢測窗，左檢測窗正對著人工缺陷模型；右檢測窗和人工缺陷模型之間是小型繞組，人工缺陷模型到左右檢測窗的距離分別約為20cm 和60cm。假設(shè)有機(jī)玻璃內(nèi)人工缺陷模型的測量分析結(jié)果為P0，左檢測窗的測量分析結(jié)果為P1，右檢測窗的測量分析結(jié)果為P2，均包含了不同缺陷模型、三個電壓等級的600 個局部放電UHF 脈沖。因此，P0 沒有折反射，P1 僅受到繞組折反射影響，P2 的UHF 傳感器與人工缺陷模型距離較遠(yuǎn)，會受到復(fù)雜的多重折反射影響，測量到的脈沖幅值也更小。分別對三組脈沖群提取如式（18）的特征，其FCM 聚類結(jié)果如表2所示。

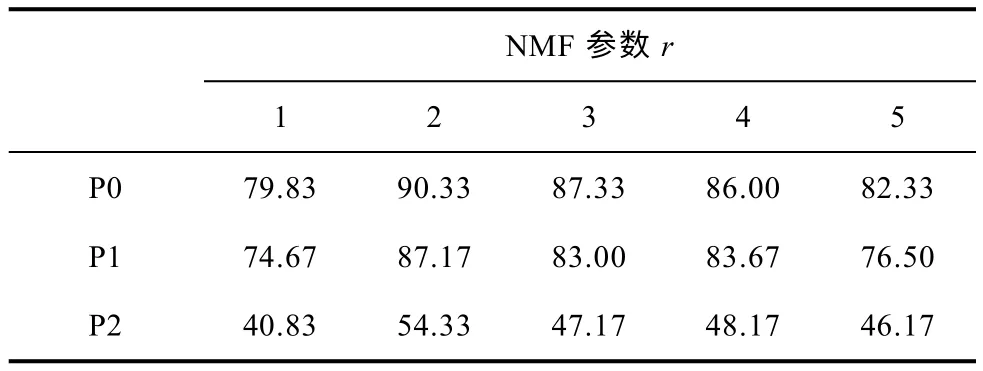
表2 不同信號傳播路徑的局部放電脈沖聚類結(jié)果（%）Tab.2 Partial discharge pulses clustering results with different signal propagation paths

由表2 可知，由于P1 僅受到了繞組折反射的影響，并且距離UHF 傳感器較近，脈沖聚類正確率雖然有一定的下降，但當(dāng)r=2 時，依然可以取得87.17%的聚類正確率。然而，由于受到復(fù)雜折反射的影響，P2 的聚類正確率降低明顯，最高僅取得54.33%的聚類正確率，表明此時ST 時頻特征已經(jīng)無法取得較好的脈沖分離結(jié)果。

7 結(jié)論

針對局部放電UHF 脈沖的特征提取與聚類分離問題，提出了基于S 變換的時頻分析與特征提取方法，并采用FCM 算法對典型局部放電源脈沖進(jìn)行了聚類分析，主要得到以下結(jié)論：

（1）引入S 變換對局部放電的UHF 脈沖進(jìn)行時頻分析，時頻幅值矩陣分布圖表明，不同放電源脈沖信號具有相互區(qū)別的時頻特征，直觀地說明了采用S 變換進(jìn)行放電源脈沖聚類分離的可行性。

（2）采用非負(fù)矩陣分解對S 變換幅值矩陣進(jìn)行分解，得到了一系列頻域基向量和時域位置向量，并對每個基向量和位置向量提取了尖銳度、導(dǎo)數(shù)平方和、信息熵及稀疏度等參量，構(gòu)成了能夠充分反映不同放電源脈沖的原始特征集。

（3）采用FCM 算法對提取的脈沖特征集進(jìn)行聚類分析。試驗(yàn)結(jié)果表明，隨著NMF 參數(shù)r 的增大，F(xiàn)CM 對不同特征集的聚類正確率呈“倒V”形變化，不同特征集的聚類正確率均大于或接近于80%，當(dāng)r 取2 時，F(xiàn)CM 算法能夠取得最高為90.33%的聚類正確率。

（4）與WVD 相比，ST 具有更高的局部放電脈沖聚類效果。當(dāng)存在局部放電信號的多重折反射時，ST 時頻特征的聚類正確率較低，無法取得較好的脈沖聚類效果。

在實(shí)際變壓器中，UHF 天線通常布置在箱體的表面，變壓器（尤其是特高壓變壓器）內(nèi)部繞組鐵心的體積特別龐大，在鐵心另一側(cè)的局部放電常常會衰減嚴(yán)重，被淹沒在環(huán)境噪聲中，難以通過鐵心，使得UHF 傳感器接收到的信號基本上為鐵心同側(cè)局部放電脈沖，與P1 情況類似。因此，本文提出的ST 時頻特征方法存在現(xiàn)場應(yīng)用的可能性，但需要進(jìn)一步的理論和現(xiàn)場試驗(yàn)驗(yàn)證。

[1]Liao Ruijin,Yang Lijun,Li Jian,et al.Aging condition assessment of transformer oil-paper insulation model based on partial discharge analysis[J].IEEE Transactions on Dielectrics and Electrical Insulation,2011,18(1)：303-311.

[2]嚴(yán)家明,廖瑞金,楊麗君,等.油浸絕緣紙局部放電損傷產(chǎn)物分析[J].電工技術(shù)學(xué)報(bào),2011,26(5)：184-191.Yan Jiaming,Liao Ruijin,Yang Lijun,et al.Analysis of damage products of oil-impregnated insulation paper caused by partial discharge[J].Transactions of China Electrotechnical Society,2011,26(5)：184-191.

[3]楊麗君,廖瑞金,孫才新,等.油紙絕緣的局部放電特征量分析及危險(xiǎn)等級評估方法研究[J].中國電機(jī)工程學(xué)報(bào),2011,31(1)：123-130.Yang Lijun,Liao Ruijin,Sun Caixin,et al.Partial discharge characteristics and risk assessment method for oil-paper[J].Proceedings of the CSEE,2011,31(1)：123-130.

[4]Mazzetti C,Frattale Mascioli F M,Baldini M,et al.Partial discharge pattern recognition by neuro-fuzzy networks in heat-shrinkable joints and terminations of XLPE insulated distribution cables[J].IEEE Transactions on Power Delivery,2006,13(4)：1035-1044.

[5]Wang M H.Partial discharge pattern recognition of current transformers using an ENN[J].IEEE Transactions on Power Delivery,2005,20(3)：1984-1990.

[6]汪可,楊麗君,廖瑞金,等.基于離散隱式馬爾科夫模型的局部放電模式識別[J].電工技術(shù)學(xué)報(bào),2011,26(8)：205-212.Wang Ke,Yang Lijun,Liao Ruijin,et al.Partial discharge pattern recognition based on discrete hidden markov models[J].Transactions of China Electrotechnical Society,2011,26(8)：205-212.

[7]Cavallini A,Montanari G C,Puletti F,et al.A new methodology for the identification of PD in electrical apparatus：properties and applications[J].IEEE Transactions on Dielectrics and Electrical Insulation,2005,12(2)：203-315.

[8]Contin A,Pastore S.Classification and separation of partial discharge signals by means of their auto-correlation function evaluation[J].IEEE Transactions on Dielectrics and Electrical Insulation,2009,16(6)：1609-1622.

[9]Hao L,Lewin P L,Hunter J A,et al.Discrimination of multiple PD sources using wavelet decomposition and principal component analysis[J].IEEE Transactions on Dielectrics and Electrical Insulation,2011,18(5)：1702-1711.

[10]Pinpart T,Judd M D.Differentiating between partial discharge sources using envelope comparison of ultrahigh-frequency signals[J].IET Science,Measurement and Technology,2010,4(5)：256-267.

[11]Tang J,Li W,Liu YL.Blind source separation of mixed PD signals produced by multiple defects in GIS[J].IEEE Transactions on Power Delivery,2010,25(1)：170-176.

[12]Gao Wensheng,Ding Dengwei,Liu Weidong.Research on the typical partial discharge using the UHF detection method for GIS[J].IEEE Transactions on Power Delivery,2011,26(4)：2621-2629.

[13]Chang C S,Jin J,Chang C,et al.Online source recognition of partial discharge for GIS insulated substations using independent component analysis[J].IEEE Transactions on Dielectrics and Electrical Insulation,2006,13(4)：892-902.

[14]Abdel Galil T K,EI Hag A H,Gaouda A M,et al.De-noising of partial discharge signal using eigendecomposition technique[J].IEEE Transactions on Dielectrics and Electrical Insulation,2008,15(6)：1657-1662.

[15]Stockwell R G,Mansinha L,Lowe R P.Localization of the complex spectrum：the S transform[J].IEEE Transactions on Signal Processing,1996,44(4)：998-1001.

[16]郭燦新,勇明,徐敏驊,等.S 變換在電力電纜局部放電信號時頻分析中的應(yīng)用[J].電工技術(shù)學(xué)報(bào),2010,25(11)：9-14.Guo Canxin,Yong Ming,Xu Minhua,et al.Application of S transform for time-frequency analysis of partial discharge signals in power cables[J].Transactions of China Electrotechnical Society,2010,25(11)：9-14.

[17]Lee D D,Seung H S.Learning the parts of objects by non-negative matrix factorization[J].Nature,1999,401(6755)：788-791.

[18]高新波.模糊聚類分析及其應(yīng)用[M].西安：西安電子科技大學(xué)出版社,2004.

[19]楊麗君,孫才新,廖瑞金,等.油紙絕緣老化狀態(tài)判別的局部放電特征量[J].電力系統(tǒng)自動化,2007,31(10)：55-60.Yang Lijun,Sun Caixin,Liao Ruijin,et al.Partial discharge features applied in aging condition discrimination of oil-paper insulation[J].Automation of Electric Power Systems,2007,31(10)：55-60.

[20]袁鵬,司文榮,李軍浩,等.局部放電脈沖的Wigner 時頻分布特性研究[J].高壓電器,2008,44(6)：524-526.Yuan Peng,Si Wenrong,Li Junhao,et al.Timefrequency characteristics of partial discharge pulse with wigner-ville distributions[J].High Voltage Apparatus,2008,44(6)：524-526.

[21]司文榮,李軍浩,袁鵬,等.局部放電脈沖的仿射類時頻分布特性研究[J].儀器儀表學(xué)報(bào),2008,29(10)：2168-2174.Si Wenrong,Li Junhao,Yuan Peng,et al.Study on characteristic of affine class time-frequency distribution for partial discharge pulse signal[J].Chinese Journal of Scientific Instrument,2008,29(10)：2168-2174.

[22]任重,董明,任明,等.沖擊電壓下SF6氣體在極不均勻場中局部放電的時頻特征[J].西安交通大學(xué)學(xué)報(bào),2013,47(8)：115-120.Ren Zhong,Dong Ming,Ren Ming,et al.Timefrequency characteristics of partial discharge of SF6gas in an extremely uneven field under impulse voltage[J].Journal of Xi’an Jiaotong University,2013,47(8)：115-120.