“RPR教學模式”的實踐與探索

金麗萍

摘 要：數學教育歷史悠久，教學模式推陳出新，在新課標的改革下，又創造了多種多樣的新模式。隨著對教學模式研究的不斷深入，教師也更加明確沒有一種教學模式可以成為固定模板，可以通用于所有數學課。因為每一堂課都有自身的特點，以“三角形的內角和”為例，打造了屬于這堂課的“RPR教學模式”。第一步，通過邏輯推理，推導出直角三角形的內角和是180°；第二步，通過動手操作的環節，驗證銳角三角形和鈍角三角形的內角和是180°；第三步，通過課外知識的拓展——法國數學家帕斯卡的發現，再次用邏輯推理法鞏固三角形的內角和就是180°。

關鍵詞：教學模式；推理；實踐；三角形；內角和

一、背景分析

中小學的教材中均有“三角形內角和定理”，即“三角形的內角和是180°”。《義務教育數學課程標準（2011年版）》在第二學段4～6年級圖形的認識中，對“三角形的內角和”提出了這樣的目標：“通過觀察、操作，了解三角形內角和是180°。”而在第三學段7～9年級圖形的性質中，提出的教學目標是：“探索并證明三角形的內角和定理。”顯然，“了解”和“證明”是有區別的。了解是指能夠從具體實例中知道或能夠舉例說明“三角形內角和是180°”的特征，而證明則要根據確實的材料判明“三角形內角和是180°”的真實性。

基于新課標對不同學段的不同目標，在教學設計過程中，就要依據教學目標來完成課堂教學。在小學階段，需要學生了解這一規律，但并非是直接告訴學生結論，而是通過學生猜想、觀察、操作等數學方法，發現三角形的內角和是180°。

二、教材分析

何為教材，顧名思義，即教學材料。教材是完成教學任務的依據，是教學過程的支架。為了上好“三角形的內角和”這一堂課，筆者橫向比較了蘇教版、北師大版和人教版三種版本的教材。

通過對三種版本教材的剖析，筆者有以下幾點思考：

第一，更傾向于北師大版和人教版的安排，對于三角形的內角和，學生最基礎的探究方法是量一量、算一算，但在蘇教版中并無體現。但蘇教版有一個知識點是其他版本不具備的，即導入時，有理論知識的鋪墊，可以讓學生更快進入角色。

第二，北師大版的引入比較卡通化，符合學生的認知結構，人教版的設計比較直接。相對而言，北師大版的探究方法更具多樣性。

第三，三種版本都同樣重視“拼一拼”的探究方法，其實這不僅僅是一種方法，更是一種轉化思想的滲透。

通過教材對比以及對其他課輔材料的深入研究，確定本次教學重點是探索和發現三角形的內角和是180°，并能利用這一知識去解決相關問題。而難點是如何去證明三角形的內角和是180°，主要依據浙師大版的探究方法。

三、“RPR教學模式”的構建

（一）理論依據

研究表明，10歲孩子的左右大腦前額皮層發育完善，孩子的天性開始消退；相反，大腦抑制能力加強；思維能力的發展處在轉折期，推理能力開始形成；培養思維的獨立性和發散性在四年級尤為關鍵。所以在這節課的設計上，我特意設計了兩次邏輯推理的環節，有意識地培養孩子的思維以及推理能力。

（二）模式構建

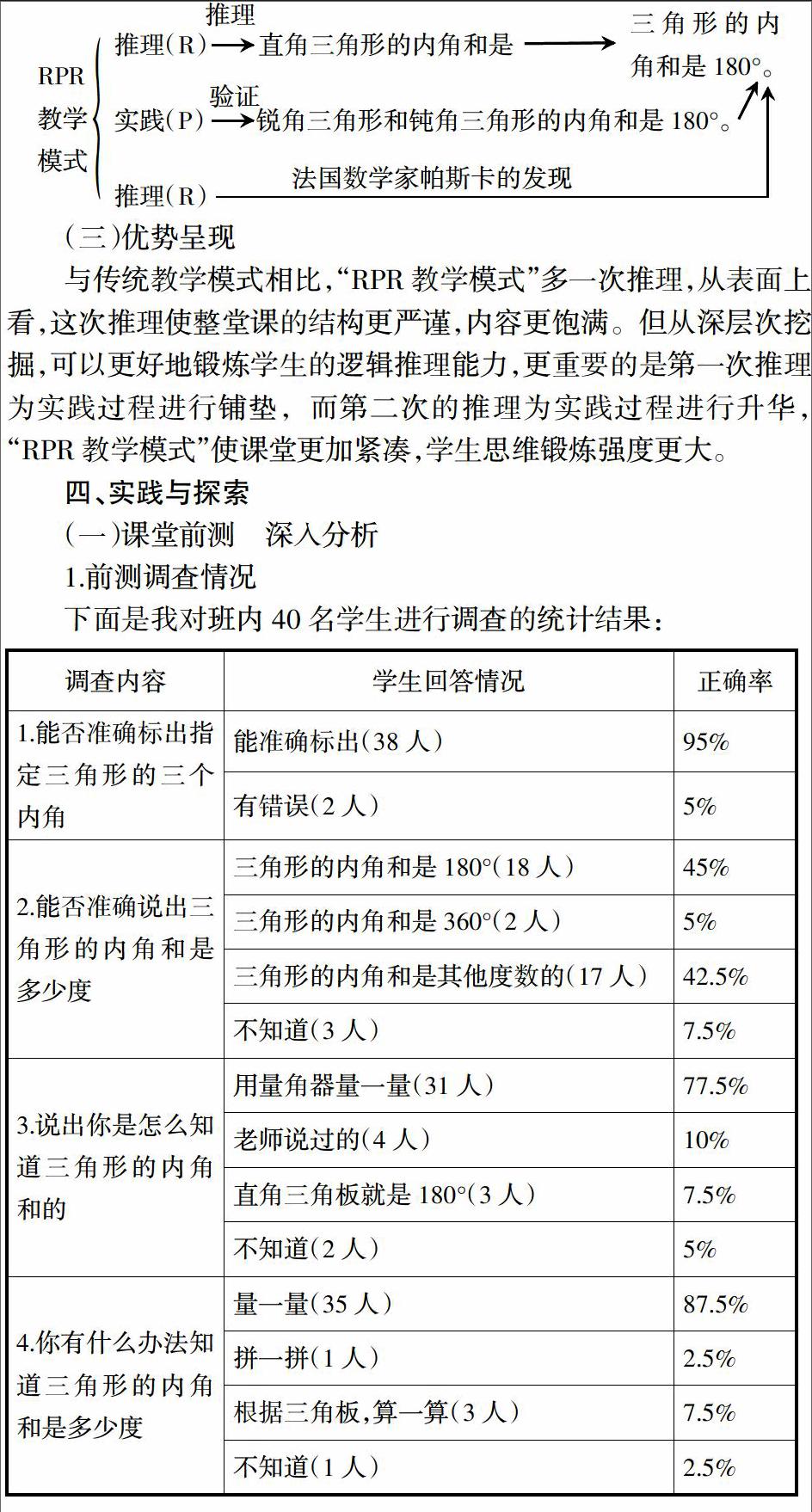
“三角形的內角和”采用了新的教學模式，比上面兩種情況更為科學嚴謹——“RPR教學模式”。到底什么是“RPR教學模式”？即Reasoning（推理）—Practice（實踐）—Reasoning（推理）三部曲。如圖所示：

（三）優勢呈現

與傳統教學模式相比，“RPR教學模式”多一次推理，從表面上看，這次推理使整堂課的結構更嚴謹，內容更飽滿。但從深層次挖掘，可以更好地鍛煉學生的邏輯推理能力，更重要的是第一次推理為實踐過程進行鋪墊，而第二次的推理為實踐過程進行升華，“RPR教學模式”使課堂更加緊湊，學生思維鍛煉強度更大。

四、實踐與探索

（一）課堂前測 深入分析

1.前測調查情況

下面是我對班內40名學生進行調查的統計結果：

2.調查結果分析

通過前測，我了解到以下三點：

第一，“三角形的內角”雖然是一個新的概念，但是通過已有的知識經驗，95%的學生已經能夠準確表達，所以在設計教學過程時，老師只需用一句話帶過。

第二，三角形的內角和是180°，全班有45%的學生能夠準確說出來，而42.5%的學生卻說出了其他答案。通過分析，主要原因是題目1中有一個具體的三角形，大部分學生都想到了用量角器去量一量，由于不可避免的誤差，以致學生回答出了五花八門的內角和度數。說明在眾多的驗證方法中，量一量的方法是最基礎的。基于學生的回答，在進行教學設計的時候，我把測量的方法放在了最前面。

第三，除了測量和根據三角板計算的方法，還有學生想到了拼一拼的方法，看看是不是一個平角，能夠想到這個方法，學生的思維算是比較活躍的。所以在進行教學設計時，我先把問題拋給學生，除了測量的方法，你還有其他辦法來驗證嗎？

（二）教學初試 產生困惑

1.發現問題

（1）巧妙設疑，揭示課題

在導入部分，我設計了以下六個問題：

①出示長方形，問這是什么？（長方形）

②你們還記得長方形有幾個角嗎？（4個）

③每個角是多少度？（90°）

④所以長方形的內角和是？（360°）

⑤課件演示，將長方形對角線等分，所得圖形的內角和是多少度？（180°）

⑥再繼續等分呢？

此時學生的思維產生碰撞，有的學生認為是90°，也有的學生說還是180°，然后揭題，今天我們就來探究“三角形的內角和”。

（2）操作交流，探究知識

①初步猜想

讓學生拿出自己的三角板，經歷算一算，拼一拼更大的三角形等過程，猜想三角形的內角和是多少度。

②測量驗證

師：怎樣驗證三角形的內角和到底是不是180°呢？你們有什么好辦法嗎？

生：量一量。

現在每個小組都有形狀不同的3個三角形。請小組合作，完成活動記錄表。

學生反饋測量的結果，并說說你發現了什么？

教學片段一：

師：通過測量，你發現了什么？（三角形的內角和有180°，也有不是180°）

師：請你觀察這些內角和不是180°的，你發現他們都和180°很？（接近）

師：對呀，其實三角形的內角和是180°，只是測量的時候會出現？（偏差）

師：是的。不同的量角器會有誤差，測量的時候也有誤差，如一個80°的內角，有同學量出來是80°，有同學量出來是81°，所以測量結果并非十分精確。現在你知道三角形的內角和是多少度嗎？（可能是180°，或者接近180°。）

學生的答案讓我很詫異，不是已經很清楚地說明了測量時是有誤差的嗎？答案的呈現不應該是齊刷刷的一句“三角形的內角和是180°”嗎？但還是有學生說“接近180°”，確實結果是學生自己親自動手測量的，所以對于自己測量出來的答案早已根深蒂固，對于誤差，學生還是不太能接受。

③拼接驗證

師：同學們，剛才我們測量的過程中，由于誤差的存在，并不能說不是所有的三角形內角和都是180°，那你還有其他辦法嗎？

請小組交流合作，請生匯報。

④課外拓展

法國數學家帕斯卡的發現。

2.引發深思

通過第一次的教學，我有了以下幾點思考：

首先，在導入部分，我故意設計一個“圈套”，讓學生產生困惑，當學生的思維產生碰撞時，讓學生動手操作，經歷探究過程去尋找答案。由于課前做過前測，知道大部分學生都會想到測量的方法，所以課前準備好三個三角形，鈍角三角形、直角三角形和銳角三角形各一個，讓學生來量一量，在量之前，一定要著重強調操作的規范性。反饋的時候，跟我預設的一樣，有180°的，也有接近180°的，

課后，我一直在思考，怎樣才能更好地解決誤差這個問題。是否應該在操作前給學生一些暗示？但又不能直接告訴他們，這讓我對本節課產生了新的困惑。

（三）挖掘教材 解決問題

1.初次推理

當我再次翻閱教本時，我發現練習十四中的第12題的第（2）小題，求長方形和正方形的內角和，這道題目對于學生而言，即使沒有學過三角形的內角和，也是會求的，因為長方形和正方形的內角都是直角，90°×4=360°，但是教本的思路肯定是讓學生分割成兩個三角形，然后180°×2=360°。突然腦海中蹦出一個想法，既然已知三角形的內角和就能求長方形和正方形的內角和，那如果知道長方形的內角和，豈不是能將它分割成兩個直角三角形，也能推出直角三角形的內角和？而且在我的教學設計中，本來就是用長方形導入的，如果能用長方形來推出直角三角形的內角和是180°，教學環節更加緊扣，而且讓學生的探究過程更加充實，多了一種探究方法。更重要的是這樣的探究方法是沒有任何誤差的。所以在第二次的教學過程中，我改變了教學過程，讓學生先用邏輯推理法，得到直角三角形的內角和是180°。

例如，12.（1）用線段分別連接長方形、正方形一組對角的頂點，分別把長方形、正方形分成了兩個什么圖形？

（2）長方形和正方形的內角和各是多少度？

教學片段二：

課件出示各種形狀的長方形和正方形：

師：同學們，今天老師請來了我們的老朋友，它們是？（長方形和正方形）

師：你們還記得長方形和正方形有幾個角嗎？（4個）

師：很好，我們就把這四個角稱之為“內角”，那你們知道長方形和正方形的內角和是多少度嗎？（360°）

師：你是怎么知道的？（一個內角是90°，4個內角就是90°×4=360°）

師：是不是所有的長方形和正方形的內角和都是360°呢？

（是的）

課件演示將所有正方形和長方形等分，變成

師：看，老師將它等分，現在我們得到了什么？（直角三角形）

師：那直角三角形內角和是多少度呢？（180°）

師：你是怎么知道的？（長方形和正方形的內角和是360°，進行等分后，就是360÷2=180°）

師：那這5個直角三角形的內角和都是180°嗎？（是的）

課件演示 變成

師：好，老師將這個由正方形等分所得到的直角三角形繼續等分，我們又得到了什么？（更小的直角三角形）

師：那你知道這個直角三角形，它的內角和是多少度嗎？為什么？

生1：90°，因為180°÷2=90°。

生2：還是180°。上面的角和下面的角都是直角等分的，所以都是45°，45°+45°+90°=180°。

師：你聽明白了？誰能再來說一遍。

師：如果老師將這個直角三角形繼續等分，請問它的內角和是多少度？（還是180°）

課件呈現大小不一、形狀不同的直角三角形。

師：通過推導，你現在知道大屏幕上的直角三角形內角和都是？（180°）

師：因為它們都可以由長方形或者正方形？（等分得到）

通過邏輯推理法，學生很好地推出直角三角形的內角和就是180°，沒有任何誤差。此時再來猜測銳角三角形和鈍角三角形的內角和是多少度時，學生的心中已經潛意識地認識到銳角三角形和鈍角三角形的內角和也是180°。當然，在學生動手操作的時候還是應該著重強調操作要求，本著科學嚴謹的態度進行操作，不得湊數，不得弄虛作假。不可否認，測量出來的結果還是會有誤差存在，但是因為有了直角三角形的內角和是180°的鋪墊，再向學生解釋內角和接近180°，是因為誤差的存在，學生顯得更難接受。

2.動手實踐

教學片段三：

師：同學們，剛才我們測量的過程中，由于誤差的存在，并不能說不是所有的三角形內角和都是180°，那你還有其他辦法嗎？

師：同學們，那現在老師給你們一點小小的提示，好嗎？請你想想看，我們能不能試著將這三個內角放到一塊去呢？

請小組交流合作，請生匯報。

為了使探究方法多樣化，除了量一量的方法，我們還應該灌輸給學生一種轉化的思想，將這三個內角轉換為一個平角，即三角形的內角和就是180°。最后通過老師的指導，學生呈現了以下三種方法。

3.再次推理

其實早在300多年前，帕斯卡就已經發現了一種“0誤差”的邏輯推理法去驗證三角形的內角和，在前面兩個環節的鋪墊下，再進行課外知識的拓展。對于直角三角形的推導我們已經掌握了，主要是在銳角三角形、鈍角三角形內做高，推出銳角三角形、鈍角三角形的內角和是180°，雖有一定的難度，但是前面的鋪墊夠扎實，學生學起來就不那么費勁了。

五、教學體會

通過本次教學，筆者有以下幾點思考。

（一）培養學生的綜合能力

RPR教學模式中，三部曲的每一個環節都在努力培養學生的能力，第一步，邏輯推理法，順利推導出直角三角形的內角和是180°。第二步，測量法，通過量一量，推出銳角三角形和鈍角三角形的內角和是180°，并且運用轉化的思想，把三個角放在一起，轉化成一個平角，同樣推出三角形的內角和是180°。在整個過程中，學生的動手能力得到了鍛煉。第三步，進行課外知識的拓展，即法國數學家帕斯卡的發現。整個探究過程，收放自如，也提供給了學生較大的自我發揮的空間，較好地鍛煉了學生的思維能力。

（二）開啟新教學模式

推理、實踐、再推理的教學模式并非通用于所有數學課，但是在動手實踐的課堂上，這樣的過程還是非常扎實的。如果沒有理論知識的鋪墊，學生直接動手操作，可能會有一定的盲目性，所以最好有一定的理論知識的灌輸，然后再動手實踐，但是往往實踐的過程是有誤差存在的，所以再一次用理論知識進行分析，最終獲得結論。通過這樣的三部曲，所得到的知識在學生心中將更加根深蒂固。

（三）推廣應用

本次探討是以“三角形的內角和”為例的，而“RPR的教學模式”既然是一種模式，自然可以推廣應用。雖然它不能適用于所有的課堂，但是圖形幾何方面的課堂還是非常值得研究和探討的，例如“平行四邊形的面積”“多邊形的內角和”等等。新的教學模式，自然有不成熟的地方，這需要慢慢磨煉，步步完善。

參考文獻：

張苾菁.從實踐操作到思想點化：《三角形的內角和》教學有感[J].小學教育教學，2011（04）.

編輯 李建軍