工科院校《概率論與數理統計》課程的教學改革與探討

張金鳳

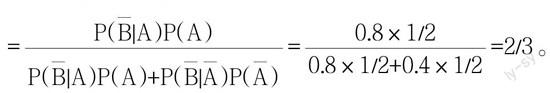
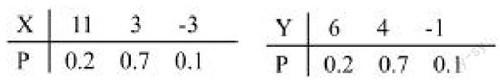
摘要：本文分析了概率論與數理統計課程的教學現狀，針對現狀提出了從案例教學、實驗教學、與專業相結合、建設網絡教學平臺等幾個方面進行改進，并適當地讓學生參與到教學環節中，達到激發學生的學習積極性和主動性，提高教學效果的目的。

關鍵詞：《概率論與數理統計》;案例教學;實驗教學;網絡教學平臺

中圖分類號：G642.0 ? ? 文獻標志碼：A ? ? 文章編號：1674-9324（2015）18-0085-02

《概率論與數理統計》是繼《高等數學》、《線性代數》之后，理工、經管等專業必修的公共基礎課程，對培養學生處理“隨機”的數學基礎知識、基本能力和綜合素質具有其他課程不可替代的作用。本文考慮到筆者所在學校學生的實際水平以及在教學過程中存在的一些問題，結合筆者多年的教學經驗，對《概率論與數理統計》課程從案例教學、實驗教學、網絡教學平臺幾方面進行探討，僅供各位同仁參考。

一、目前教學現狀

筆者根據多年的《概率論與數理統計》教學經驗對目前教學中普遍存在的一些問題進行總結，主要有四個方面：（1）教學內容一成不變，一本教材多專業通用，例題與練習不能很好地結合學生專業特點，致使學生不了解《概率論與數理統計》對后續課程以及專業課的影響和作用，學習時缺乏熱情和主動性。（2）教學手段單一，大多采用板書+多媒體課件的形式。一些教師過度依賴多媒體課件，雖然緩解了教師書寫的壓力，但由于形式過于呆板，課件內容固定，教師不能靈活地調整教學內容，學生處于被動的聽課狀態。（3）現有相關教材多注重概率統計的理論，而對如何操作軟件來解決實際問題介紹得很少。由于學時有限，教師也將精力主要放在理論內容的講解和計算上，使得學生對課程的理解停留在理論層面上，造成課程理論與實踐相脫節。（4）理工科的《概率論與數理統計》多以45學時為主，課程安排一般為兩周三次課，時間安排不夠緊湊。學生在課后對課上的內容只能憑記憶進行總結和消化吸收，如果不能及時復習內容，就會造成知識的積壓，影響后面的學習。面對以上教學中存在的問題，如何有效地提高課堂的教學效果，激發學生的學習主動性，是教師面臨的亟待解決的問題。

二、改善教學效果的幾點建議

1.將案例教學融入課堂，激發學生的學習興趣。由于概率論與數理統計的實用性強，生活中的許多現象均可運用概率統計的知識和方法來解釋。教師在講授某個知識點時，不妨將相關的生活實例融進教學中，激發學生學習的興趣，使得抽象的定義、公式更為直接易懂，有助于學生對知識點的理解和掌握。比如在介紹貝葉斯公式時，可借用一個大家耳熟能詳的“狼來了”的故事來理解和體會貝葉斯公式。故事講的是一個放羊的小孩，在兩次欺騙村民說“狼來了”后，第三次狼真來了，而沒人相信的事。接下來利用貝葉斯公式進行分析。設事件A表示小孩說謊話，事件B表示狼來了。先做一些假設：村民對小孩的信任程度一般，即P（A）=P（■）=1/2，而說謊的小孩喊狼來了的概率P（B|A）=0.2，說真話的小孩喊狼來了的概率P（B|■）=0.6。那么當小孩第一次說謊喊狼來了的時候，村民對小孩說謊的印象P（A|B）由貝葉斯公式計算得：P（A|■）=■=■=2/3。這時注意到村民對小孩的說謊的概率由0.5上升到0.667，可記P（A）=2/3，P（■）=1/3。小孩第二次說謊喊狼來了的時候再次利用貝葉斯公式得P（A|■）=0.8。通過以上的計算表明，在村民上過兩次當后，對小孩說謊話的概率已經由0.5修正到0.8，面對如此高的說謊概率，試問村民聽到第三次小孩喊狼來了，怎么還會去上山呢？可見人與人之間的信任禁不起謊言的消磨。對生活中一個大家都熟識的寓言，通過全概率公式的分析，將結論量化，更容易理解。再比如講解數學期望這個重要的概念時，可以將期望概念的起源故事即“賭資分配問題”介紹給學生。所謂的“賭資分配問題”是17世紀中期一位賭徒向數學家帕斯卡提出了一個困擾他很久的問題：甲乙兩賭徒相約，利用擲硬幣的方式進行賭博，各出50法郎，誰先贏三局即可得全部賭本100法郎。當甲贏了兩次，而乙只贏一次時，因事需終止賭博，那么賭金如何分配呢？當這個問題在課堂上提出時，不少學生產生了興趣，并給出了自己認為合理的答案，這時教師進而引出正確的解法。1654年帕斯加提出最多只需再玩兩次就可結束此次賭博，這兩次可能出現的結果分別為：甲甲、甲乙、乙甲、乙乙。對于甲來說只要出現四種可能結果的前三種，甲都勝出，故甲得100法郎的概率是3/4，得到0法郎的概率為1/4，從而甲應期望得到100×3/4+0×1/4=75法郎。其意指，若再繼續此種賭博多次，甲每次平均可得75法郎。從這個解法中引出數學期望的概念即E（X）=x1p1+x2p2。除引用有趣的案例外，教師還可以盡可能地讓學生參與到教學環節中，以激發學生學習的積極性和主動性。

2.讓實驗教學走入課堂，提高學生實際動手操作的能力。《概率論與數理統計》是一門應用性、實踐性很強的學科，其在各方面的應用性可以通過例題呈現給學生，而實踐性在現有的教學環節中并沒有得到充分的體現，學生不能利用所學的知識解決一些簡單的概率統計問題。教師在課堂上可以選擇一些題目進行簡單的操作，向學生展示概率計算和統計分析的基本步驟。課后提供相應的練習，促使學生在學習中較自然地掌握計算機的實現過程，較好地解決了實踐與教學相脫節的問題。

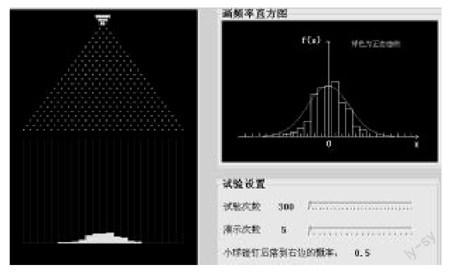
3.充分利用現代化教學手段，提高課堂教學效果。課堂教學多采用板書+多媒體課件的形式，在以教學效果為主的前提下，二者可以相互補充，揚長避短。無論是板書還是多媒體課件的使用，都要有個度，比如定理的推導和例題的計算，適合用板書來講解，達到師生互動的良好效果。而定義、定理的陳述、圖形的演示可以利用多媒體，一方面省去教師書寫的壓力，另一方面借助多媒體展示圖形能更好地理解問題。此外也可以考慮將一些現代化的教學手段和成果穿插在教學中，一定程度上可以提高教學效果。比如在介紹獨立同分布的中心極限定理時，不妨先借助著名的高爾頓釘板試驗，通過不斷地調整試驗次數和演示次數，將小球堆積的效果圖與正態分布曲線相比較，從而分析引出中心極限定理內容，可以幫助學生更形象、直觀地理解中心極限定理的思想。

4.結合專業特點，精選例題。為了更好地將《概率論與數理統計》課程與學生專業相結合，教師可以根據所教學生專業的特點，選擇和專業貼合較近的例題，這樣學生在學習時，能較好地了解該課程對后續專業課的影響和作用。比如給金融、經濟專業的學生上課時，關于數學期望和方差的概念，不妨可以通過一個關于風險投資的問題來理解。例題：某人有一筆資金，可投入兩個項目：房地產和開商店。其收益都與市場狀態有關。若把未來市場劃分為好、中、差三個等級，其發生的概率分別為0.2、0.7、0.1。通過調查，該人認為購置房地產的收益X和開商店的收益Y的分布如下表，問該人資金應該流向何方？

先計算數學期望（即平均收益）E（X）=4（萬元），E（Y）=3.9（萬元）。從平均收益看，購置房地產利益比開商店多0.1萬元。再計算兩者的方差，D（X）=15.4，D（Y）=3.29。方差越大，收益的波動越大，從而風險就越大，顯然購置房地產的風險要比開商店大得多。綜合考慮，該投資者還是選擇開商店。

5.建立網絡教學平臺，引導學生自主學習。網上資源豐富，但學生想找到合適的內容就不太簡單，而且還要花費大量的時間。所以筆者依托學校提供的平臺建設適合各階段學生的網絡教學平臺。網絡教學平臺包含教師精心選取的內容，既可以節省學生的時間，又可以有針對性地引導學生自主學習。網絡教學平臺主要包括概率統計的各章課件、校級教改成果-概率論與數理統計習題課視頻、各章節知識點總結、各章習題答案、歷年期末試題、考研輔導材料以及國內一些大學歷年期末試題幾個模塊。其中概率論與數理統計習題課的視頻可供學生隨時觀看，作為課堂教學的補充，而且該形式不受時間、地點的限制，從而將學生由被動的課上學習轉化為課下的主動學習，解決了課下每周僅有一次答疑時間的局限性，學生可以根據針對個人情況有選擇地學習。《概率論與數理統計》網絡教學平臺的建立，較全面、完整地將《概率論與數理統計》課程組織在一起，使學生在利用平臺學習時，根據自身學習情況，有針對性地選擇，并輔以習題來鞏固和提高理論知識，通過試卷檢驗自己的學習效果。

三、結論

本文對《概率論與數理統計》課程的教學現狀進行分析，從案例教學、實驗教學、網絡實驗平臺等幾個方面進行相應的改善，教學效果在一定程度上得到了提高，同時了也激發了學生的學習積極性。當然，教學改革是無止境的，要根據學生層次、教學內容等不斷地進行調整，以達到較好的教學效果。

參考文獻：

[1]茆詩松，程依明，濮曉龍.概率論與數理統計教程[M].北京：高等教育出版社，2004.

[2]朱淑芹，班朝磊.《概率論與數理統計》教學改革探討[J].教育教學論壇，2014，（45）.

[3]張瑞亭.對概率統計教學中若干問題的探討[J].教育教學論壇，2014，（02）.