大展弦比機翼翼梢裝置性能特性研究
王超,呂莉莉,杜麥勝,劉毅
(中航飛機股份有限公司研發中心總體氣動設計研究所,陜西漢中723000)
0 引言
減小飛機阻力是提高空氣動力效率的一個關鍵因素,誘導阻力是飛機阻力的重要組成部分。一般來說,飛機巡航時的誘導阻力占總阻力的30%左右[1],在低速大迎角飛行時所占的比重更大。因此,減小誘阻以提高空氣動力效率的研究受到高度的重視[2]。空氣動力學的機翼理論指出,增大機翼的展弦比能減小誘導阻力,但大展弦比對結構不利,機場環境對機翼展長也有一定的限制;因此,通過翼尖設計以及加裝翼梢裝置來改善翼尖區的氣流流動和減阻是減小誘阻的重要手段。
多年來,國內外學者從理論計算、風洞試驗、飛行試驗等方面對各類翼梢裝置作了大量的基礎性及應用性研究,一些研究成果投入實際應用并取得了明顯的效果[2]。NASA 研究表明[3],KC-135 加裝翼梢小翼使飛機總阻力下降7%,升阻比提高5% ~8%。B737-800加裝融合式翼梢小翼[4]使航程增加約240~350 km。但國內外研究多集中于中等及小展弦比機翼的翼梢裝置研究,未見對大展弦比(10以上)機翼飛機加裝翼梢裝置的研究及使用報告。
某四發渦槳飛機采用了低速大展弦比的機翼布局,展弦比約為12,升阻比約為15。由于高空/高原動力裝置功率衰減大,極大地限制了高原機場的起降能力和航路越障能力,而動力裝置研制周期長,短期有效的方法是提高飛機的升阻比。根據理論分析[5],翼梢裝置對大展弦比飛機的效果不如小展弦比飛機明顯,但由于該型機巡航升力系數較大,誘導阻力正比于升力系數的二次方,故飛機仍具有采用翼梢裝置減阻的潛力。本文研究了在大展弦比飛機采用翼梢裝置的可行性,提出翼梢裝置設計優化方法,并以風洞試驗數據為依據,對大展弦比機翼飛機的飛行性能提升進行計算驗證并尋找最優方案。
1 翼梢裝置設計及氣動效率分析
1.1 翼梢裝置提高氣動效率原理
飛機飛行中的阻力主要有壓差阻力、粘滯阻力和誘導阻力。壓差阻力和粘滯阻力會很快轉化為熱能,可以改變的只有誘導阻力。而機翼所產生的升力,一部分用于消除誘導阻力,另一部分用于提供升力。誘導阻力越小,則提供的升力越大。減小誘導阻力最直接的方法是通過增加機翼的翼展來實現的,但對于部分大展弦比機翼,過多的增加機翼的翼展將帶來如結構重量、氣動彈性等問題[6]。
翼梢裝置的主要功能是減小飛機的誘導阻力。加裝優化設計的翼梢裝置,機翼有效展弦比提高,升阻比增加。翼梢裝置應用于展弦比A值較小的飛機顯然具有更大的減阻潛力,對于低速大展弦比機翼的飛機仍能有效減小誘導阻力、提高升阻比,從而提高飛機的起飛性能、爬升性能和續航性能。
1.2 影響飛行性能的因素
對起飛性能影響較大的因素包括動力裝置的可用拉力、飛機的升阻特性、飛機的失速速度等。簡化的起飛滑跑距離計算公式[7]為:
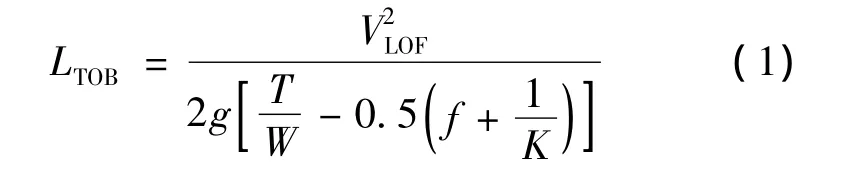
式中:LTOB為起飛滑跑距離;VLOF為起飛離地速度;g為重力加速度;T/W為起飛推重比;f為摩擦系數;K為升阻比。在其他狀態相同的情況下,升阻比越大,離地速度越小(最大升力系數越大),起飛滑跑距離越短。
影響飛機爬升性能的主要因素是飛機的剩余功率和爬升方式。
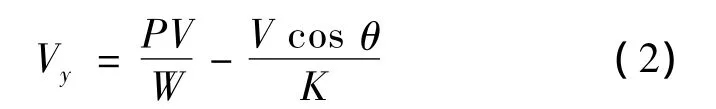
式中:P為爬升功率;W為爬升重量;V為爬升速度;θ為爬升角。爬升方式一定時,升阻比K增大,飛機爬升率增加,飛機的升限也有所提高。
巡航性能直接受小時耗油量qh=WqNh/K的影響,航程 L、航時 t計算公式[8]為:
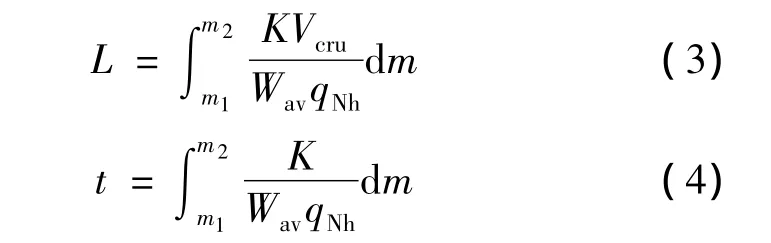
式中:m1,m2為巡航開始和結束時的重量;Wav為平均巡航重量;Vcru為巡航速度;qNh為單位小時耗油率。巡航狀態升阻比增大,航程、航時均有所提高。
1.3 翼梢裝置設計
長期以來,人們一直力圖通過改變機翼翼尖處的幾何形狀,研究減小誘導阻力的有效方法。展向延伸機翼翼尖是方法之一,還有修改翼尖形狀和改變其位置等其他措施[9]。研究發現,用非平面的翼梢升力系統比簡單的翼尖延伸設計能達到更好地減小誘導阻力的效果,如翼梢小翼。翼尖設計可分為翼尖修形和加裝翼梢裝置兩類,前者主要有剪切翼尖、拋物翼尖和雙曲翼尖等;翼梢裝置又分為主動式和被動式,如加裝渦流裝置和翼梢小翼。翼梢裝置的重量對結構和機翼彎矩不利,此外翼梢裝置的存在還會對飛機的穩定性和操縱性有影響,特別是方向穩定性[10]。
結合某型飛機大展弦比機翼(見圖1)的特點,在最大程度提高升阻比的前提下,按照對機翼根部彎矩增加量相同的原則,充分考慮翼梢裝置對重量及橫航向的影響,設計了不同的翼梢裝置外形方案,通過對比分析,尋找最佳方案。

圖1 原機翼Fig.1 Original wing model
方案1:通過在翼尖加裝翼梢小翼(見圖2),使機翼的半翼展增加10%,外傾角為15°,前緣后掠角為40°,小翼根弦前端位于機翼尖弦長33%處,避開機翼尖弦最大厚度位置,以期提高小翼效率。翼梢小翼翼型彎度大于機翼翼型,翼型厚度小于機翼翼型,這樣既可以提高低速升力特性,也可以提高有效的法向力,使小翼氣流分離遲于機翼。

圖2 翼梢小翼Fig.2 Winglet model
方案2:取消原機翼翼尖,機翼沿肋等百分線展長增加5%,展弦比增加7%,將原翼尖按照比例縮放,安裝在新的機翼梢部(見圖3)。通過增加展弦比增大氣動效率。

圖3 機翼翼尖延伸Fig.3 Wingtip extension model
方案3:取消原機翼翼尖,設計新的低阻翼尖方案(見圖4),展長增加4.2%,展弦比增加6.5%。通過將原梯形的翼尖外形修成曲線外形(三次曲線)改善機翼翼尖的氣動效能。

圖4 減阻翼尖Fig.4 Drag-reduction winglet model
最后通過風洞試驗對不同方案的氣動效果進行了驗證,改善效果如表1所示。
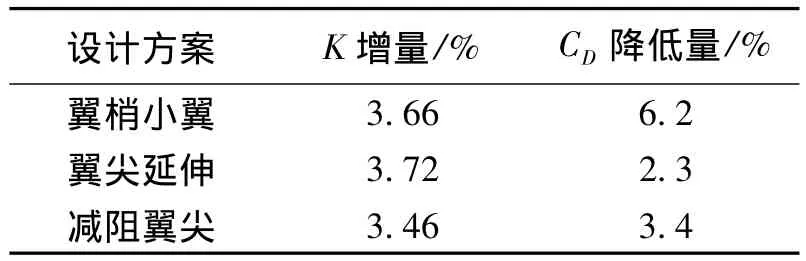
表1 氣動改善效果Table 1 Effect of aerodynamics improvement
2 翼梢裝置對飛行性能的影響
2.1 性能特性影響
加裝翼梢裝置的主要功效在于通過有效減小誘導阻力和提高升阻比,從而提高飛機的飛行性能。特別對于高原高溫條件下的起飛有著明顯的改善作用。
高原機場空氣密度小,加之高原機場地面輻射熱的影響,場面氣溫高,起飛和滑跑距離會增加1.5~2.0倍[11]。發動機起動較平原機場困難,不同高度、溫度下動力裝置推力變化較大,隨著溫度、高度增加,發動機扭矩和拉力值減小,起飛著陸滑跑距離、爬升率和實用升限均減小。因此,可通過計算分析高原高溫條件下加裝翼梢裝置的性能變化,對各優化設計的翼梢裝置方案進行有效評估。
2.2 起飛滑跑距離
以機場標高3 000 m、起飛重量65 t,大氣溫度22.5°C為例,采用式(1)計算不同方案對起飛滑跑距離的影響(見圖5)。某型飛機原機翼方案的起飛滑跑距離為4 988 m,而加裝了“翼梢裝置”后,起飛滑跑距離縮短了275~620 m,特別是加裝優化設計的低阻翼尖后,起飛性能提升明顯。

圖5 不同翼梢裝置對L TOB的影響Fig.5 Influence of different wing tip device on L TOB
2.3 跑道長度限制的最大起飛重量
以機場標高3 000 m、大氣溫度22.5°C、機場跑道長度4 000 m為例計算飛機的平衡場長和起飛限重(機場起飛限重見圖6),其中原機翼起飛重量限制為59 t,安裝“翼梢裝置”后,起飛重量增加2~3 t,特別是加裝優化設計的減阻翼尖后,最大起飛重量達到62.5 t。
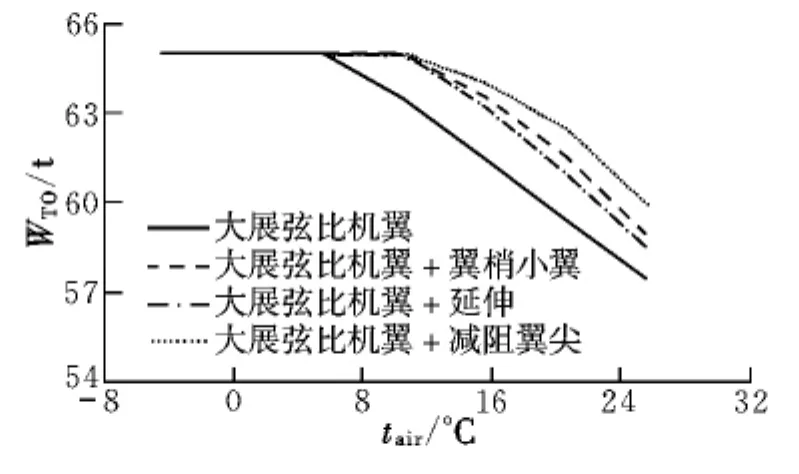
圖6 不同翼梢裝置對最大起飛重量的影響Fig.6 Influence of different wing tip device on maximum take-off weight
2.4 航線最低安全高度限制的最大起飛重量
對于飛越高山地區的航線,航線最低安全高度會限制飛機的最大起飛重量,這是因為巡航時一臺發動機停車后,飛機的改平高度降低。CCAR121部和相關軍用標準均要求多發飛機航路飛行時必須考慮到一臺發動機故障停車的可能性,要求單發停車后的改平高度(升限)大于航路最低安全高度,單發停車后升限越高,飛機任務執行能力/運載力越強。采用式(2)及數值積分的方法,計算了大氣溫度ISA+30°C、某型機不同方案飛機單發停車后的實用升限(見圖7)。計算結果表明,安裝“翼梢裝置”后,飛機單發失效后實用升限提高了120~270 m,相對于同樣的航路最低安全高度,飛機的最大起飛重量提高約2 t,顯著提高了飛機在高原航線、高溫季節執行任務的能力。
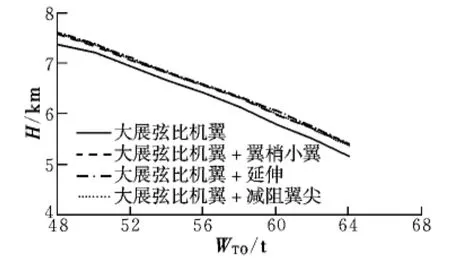
圖7 不同翼梢裝置對單發失效爬升高度的影響Fig.7 Influence of different wing tip device on climb height with one engine failed
2.5 續航性能
飛機的續航性能直接關系到飛機營運經濟性和營運能力,采用式(3)和式(4)計算了某型機加裝翼梢裝置的續航性能(見表2)。計算結果表明,翼尖加裝翼梢裝置以小重量的代價增加飛機的升阻比,提高了巡航效率、降低了油耗,航程與航時均提高了2%左右。
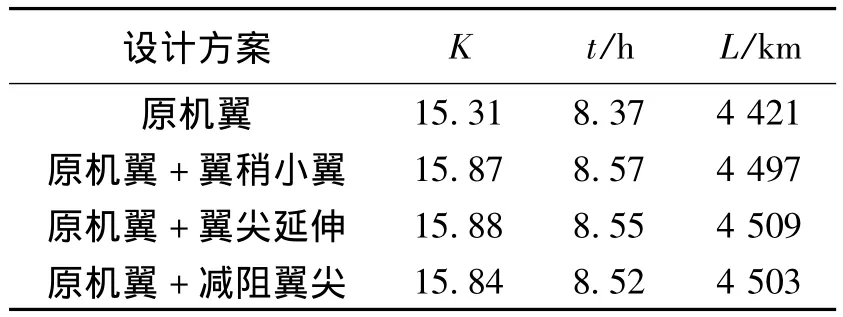
表2 續航性能改善Table 2 Improvement of endurance performance
3 結束語
本文對大展弦比機翼的低速飛機加裝翼梢裝置的可行性進行了研究。研究結果表明,大展弦比機翼的低速飛機加裝翼梢裝置可有效減小誘導阻力、提高升阻比,從而提高飛機的起飛性能、航路越障限制的最大起飛重量和續航能力,不失為改善飛行性能的有效手段。通過對不同翼梢裝置的特性分析,為進一步優化翼梢裝置提供了技術基礎。
[1] Sloff JW.A survey of computational methods for subsonic and transonic design[C]//Proceeding of the first conference on inverse design concepts and optimization in engineering(ICIDESI).1984:1-68.
[2] 朱自強,吳宗成.現代飛機設計空氣動力學[M].北京:北京航空航天大學出版社,2005:182.
[3] Grignon PM,Woodziak JR,Fadel G M.Bi-objective optimization of components packing using a genetic algorithm[R].AIAA-96-4022,1996.
[4] Powell M J D.An efficient method for finding the minimum of a function of several variables without calculation derivatives[J].Computer Journal,1964(7):155-162.
[5] Rayer D P.Aircraft design:a conceptual approach[M]4th ed.New York:American Institute of Aeronautics and Astronautics,Inc.,2006:69-71.
[6] Mattos B S.Considerations about winglet design[R].AIAA-2003-3502,2003.
[7] 方振平.飛機飛行動力學[M].北京:航空航天大學出版社,2005:82.
[8] 丁松濱.飛行性能與飛行計劃[M].北京:科學出版社,2013:51.
[9] Jameson A,Vassberg J C.Computational fluid dynamics for aerodynamic design:its current and future impact[R].AIAA-2001-0538,2001.
[10] Zbigniew M.Genetic algorithm+data structure=evolution programs[M].New York,Springer,1992.
[11]蔡良才,鄧學鈞.飛機極限起飛重量和決斷速度的確定[J].東南大學學報,1997,27(1):136-138.

