基于沖突距離的空中高速路換道模型

王莉莉，劉洋

(中國民航大學天津市空管運行規劃與安全技術重點實驗室，天津300300)

0 引言

隨著我國航空運輸業的不斷發展，有限的空域變得越來越擁擠，交通流量也變得日益飽和［1］。民航工作者開始致力于研究空域結構和管制方式的變革，空中高速路成為解決這些問題的一種新途徑。

歐委會(ECAC)于1999年提出了“歐洲天空一體化”的構想，其中高速路是主要設計內容，定性地給出了空中高速公路結構和位置設置的建議［2］。文獻［3］分析了空中高速路從設計到運行需要解決的8個主要問題。文獻［4］提出了我國空中高速路網絡的布局與結構。文獻［5］研究了空中高速路的流量模型。文獻［6］建立了基于CNS性能的平行航路縱向碰撞風險評估模型，分析了通信、導航和監視誤差，推導出平行航路縱向重疊概率的計算公式。文獻［7］針對京滬平行航路的設計、必要性進行了分析，并對平行航路可操作性和實用性進行了探討。然而，鮮有對空中高速路平行航路換道模型的研究。

我國空中高速路的研究還處于發展階段，還有許多問題亟需解決。航空器進行換道操作會引起交通擾動，影響航路交通流的穩定性、通暢性。當遇到高峰時段時，換道操作不當會引起航路更加擁擠。另外，管制員管制航空器進行換道操作直接關系到航路交通的安全性，錯誤的換道操作將使航空器處于潛在的沖突危險之中。

本文以空中高速路中平行航路為例，研究航空器在平行航路換道的最小沖突距離(Minimum Confliction Spacing，MCS)模型，分析影響最小沖突距離的各種因素，為安全換道行為提供理論基礎。

1 空中高速路理論

1.1 空中高速路基本路段

空中高速路是由三種不同類型的路段組成的，基本航路段、交匯區、匝口共同組成了復雜的空中高速路系統。高速公路基本路段是指不受匝口附近的合流、分流以及交織影響的航路段部分。它處于任何匝口或交織區的影響區域之外，是空中高速路的主體部分(見圖1)。由于交匯區合流、分流換道操作較復雜，本文僅研究空中高速路基本航路段的換道行為。

1.2 空中高速路平行航路

空中高速路平行航路是指平行航路內邊界之間間隔不小于18.5 km，并且只考慮6.6 km以上高空管制空域內單向運行的平行航路［8］。平行航路的側向及縱向間隔標準暫按將要建立的京滬平行航路間隔標準，即側向及縱向間隔標準均為10 km［9］。本文僅研究飛行階段占用相同高度層的平行航路，不考慮垂直間隔。在飛行過程中，飛機之間應保持一定的間隔，當兩機間隔小于最小間隔標準時，存在相撞可能，則認為飛機之間發生了碰撞沖突。

2 平行航路換道模型

2.1 模型條件

2.1.1 航空器碰撞沖突模型定義

由于只考慮側向間隔與縱向間隔，以飛機質心為中心建立兩個長方形(見圖2)，稱為方a、方b。方a為飛機幾何尺寸，方b為沖突風險區，A機的沖突風險區稱為A區，B機的沖突風險區稱為B區，方a到邊界距離為最小間隔的一半。若兩個方b不接觸，則認為相撞率為0;若兩個方b觸碰重疊，兩機之間小于最小安全間隔，則認為產生飛行沖突;若兩個方a接觸重疊，則認為兩機相撞。為了不發生沖突，前后兩航空器的沖突風險區之間沿飛行方向必須保持的最小飛行間距稱為最小沖突距離。圖中，l和w分別為沖突風險區長度和寬度。

2.1.2 換道環境

航道變換是一個復雜的過程，圖3是一個較為典型的換道環境，S航空器從N道的S1區與S4區之間變換至M道的S2區與S3區之間。

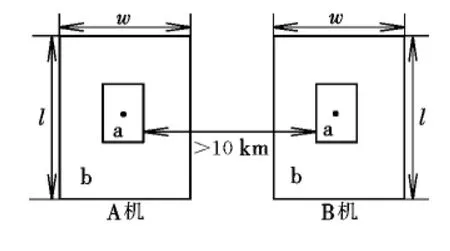
圖2 兩機碰撞沖突模型Fig.2 Collision conflict model between aircraft

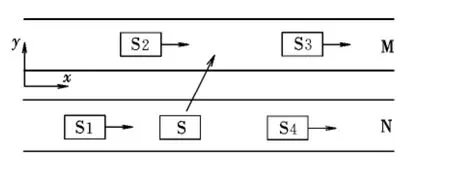
圖3 航道變換環境Fig.3 Environment of lane changing

2.1.3 假設條件

本文僅考慮雙行航路單次換道的情況，多次換道可認為是其行為的重復。由于航路中的換道與地面換道不同，不僅需要在管制員的指令下進行，同時受到諸多因素的影響，因此作如下假設［9］:

(1)在換道過程中，除換道航空器以外，其他航空器保持勻速飛行且在航路中央;

(2)航空器在換道過程中，橫向速度不影響縱向速度的變化;

(3)不考慮高空風影響;

(4)航空器換道行為只考慮航空器自身，不考慮駕駛員、管制員等人為因素的影響;

(5)研究S區時，無需考慮跟隨其后的S1區的影響。

2.2 平行航路換道運動學分析

2.2.1 換道航空器參考點定義

如圖4所示，設S航空器的沖突風險區(S區)4個角分別為R1，R2，R3，R4。若已知左前角R3點的橫向位移為y2(t)，則其他三點的橫向位移［10］可以采用一階近似得出:

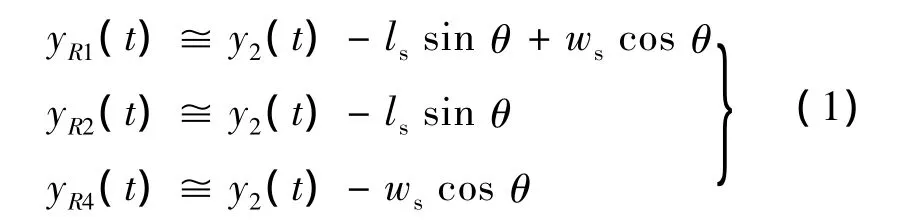
式中:ls為S區的長度;ws為S區的寬度;θ為S區軌跡切線與x軸的夾角。

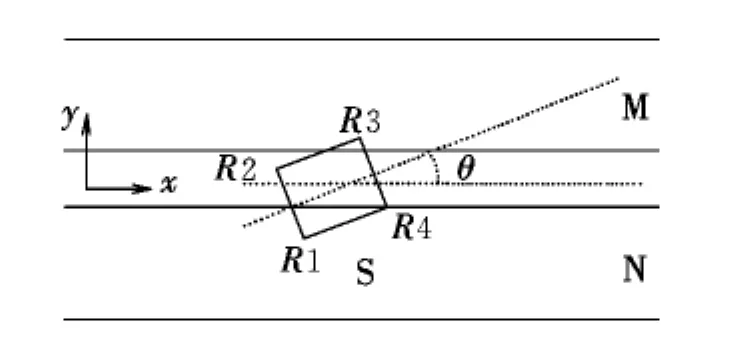
圖4 S航空器沖突風險區參考點Fig.4 Reference point of Saircraft conflict risk area

2.2.2 換道過程的運動學分析

假設:在t=0時，管制員給S航空器下指令進行換道;S航空器的橫向加速度為a2;除S航空器外，其他航空器在航路中直線平穩飛行，橫向加速度均為0。

以S航空器R3點為參考，當S航空器完成換道行為時，其橫向移動距離為L。在整個換道過程中，a2先增大后減小;當a2達到最大時，航空器位于L/2處。S航空器換道軌跡如圖5所示。

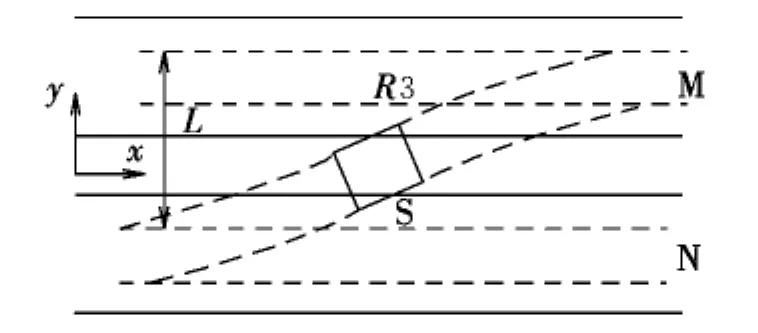
圖5 S航空器換道軌跡Fig.5 Lane changing trajectory of Saircraft

假設S航空器進行平穩的換道操作，橫向速度V2符合正弦波特性，則a2符合余弦波特性［11］。設:

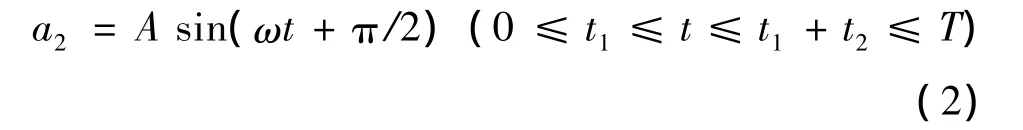
式中:A為待定系數;ω=2π/t2;t1為S航空器施加橫向加速度之前的調整時間;t2為S航空器施加橫向加速度的時間;T為S航空器完成換道時間。則:

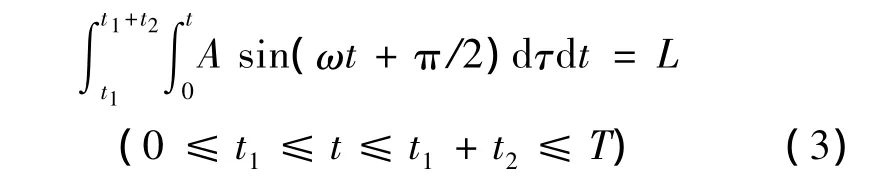
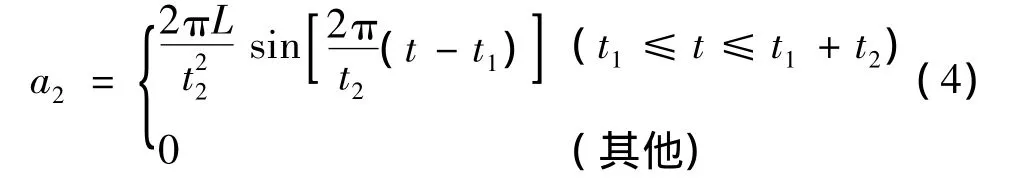
對式(4)積分，得到V2(t)為:

再積分得到S航空器橫向位移y2(t)為:

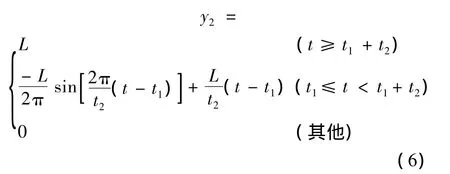
2.3 最小沖突距離建模

航空器開始進行換道操作時，由于高空中飛機速度快，兩航路之間距離較近，故假定航空器進行換道操作時的縱向速度變化很小，加速度均為零。本文主要以S航空器與S4航空器之間的最小沖突距離為例，論述最小沖突距離建模方法。

如圖6所示，設D為t=0時S航空器的沖突風險區(S區)和S4航空器的沖突風險區(S4區)的橫向內側間距，H為S4區左側縱向切線。

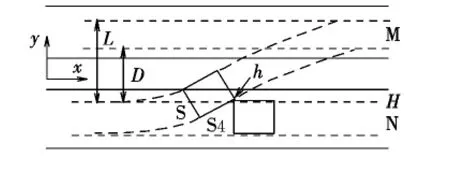
圖6 S區與S4區沖突示意圖Fig.6 Conflict schematic diagram between Sarea and S4 area

設S航空器在t=t1時進行換道操作，其沖突風險區右前角(R4點)通過H線，與H線相交于h點，th+t1為S區移動到h點時間。當t1＜t＜th+t1時，S區易與S4區發生斜向沖突。根據式(1)，當t=th+t1時，R4點的橫向位移滿足:

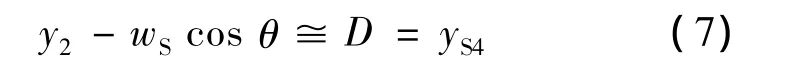
根據式(1)，式(7)又可以表示為:

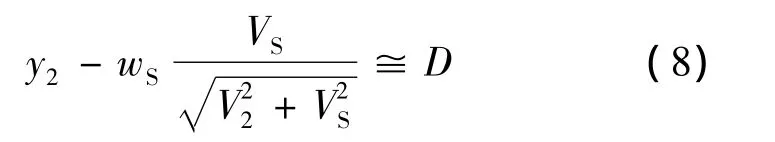
聯立式(5)、式(6)和式(8)可求得th+t1值。

S區與S4區不發生沖突的條件為:

式中:wSsinθ是保證在［t1，th+t1］時間內 S區R4點與S4區后部不發生接觸的重要指標。在［0，th+t1］時間段，sinθ最大值在t=th+t1時刻取得。令，則式(9)簡化為:

令D(t)為S區與S4區的縱向距離，表示為:

在t≤th+t1時，只要D(t)＞0，就不會發生任何形式的沖突。于是式(11)又可以表示為:

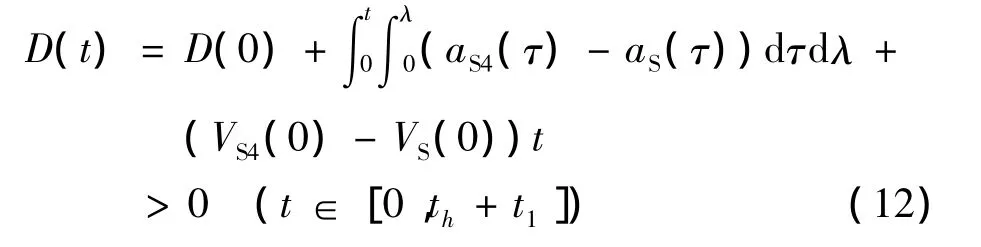
其中:

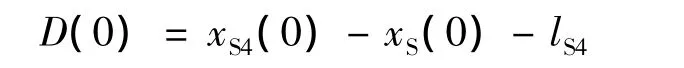
D(0)的最小值即換道時S區和S4區不發生任何沖突的最小沖突距離DMSC(S4，S):

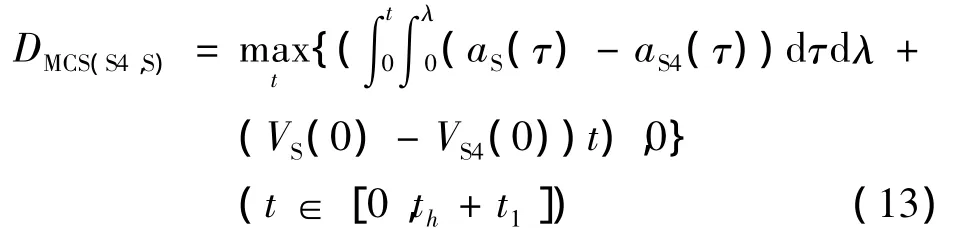
從式(13)中可見，S區和S4區的最小沖突距離DMSC(S4，S)主要與兩航空器之間的相對初速度、相對縱向加速度以及時間th+t1有關。

簡化式(12)，可得S區與S4區不發生沖突的條件為:

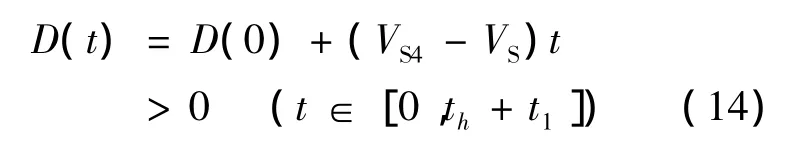
則:

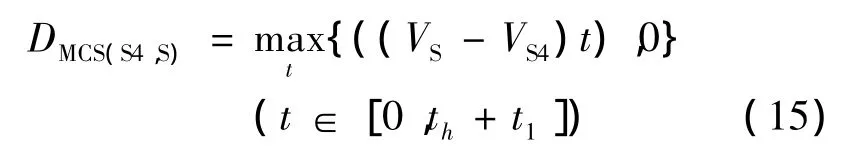
由于S區和S4區的相對速度始終為常數，式(15)可寫為:

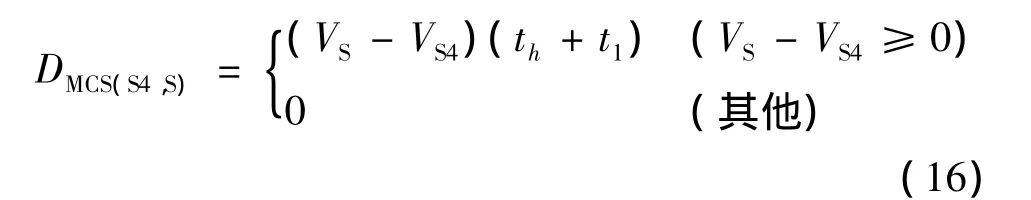
同理可得，S航空器與S3航空器之間的最小沖突距離為:

S航空器與S2航空器之間的最小沖突距離為:

3 仿真計算

設航路寬為20 km，航路間隔為18.5 km;航空器縱向及側向間隔均為10 km，沖突風險區長度l和寬度w均為10 km。S航空器以B737-800為例，巡航速度取Vs=800 km/h，L=38.5 km，飛機轉彎角度一般不宜過大，取θ為30°。

根據式(7)求得 V2=462 km/h，T=L/V2=300 s。取 a2=2 m/s2，則 t2=V2/a2≈64 s。仿真結果如圖7所示。圖中:橫坐標分別表示S區與S4區、S3區的縱向速度差，S2區與S區的速度差;縱坐標D分別表示S區與S4區、S3區、S2區之間的初始縱向距離。例如:當VS－VS4=10 m/s時，對應縱坐標為D=300 m，則當D＞300 m時為安全沖突距離，D＜300 m為不安全沖突距離。

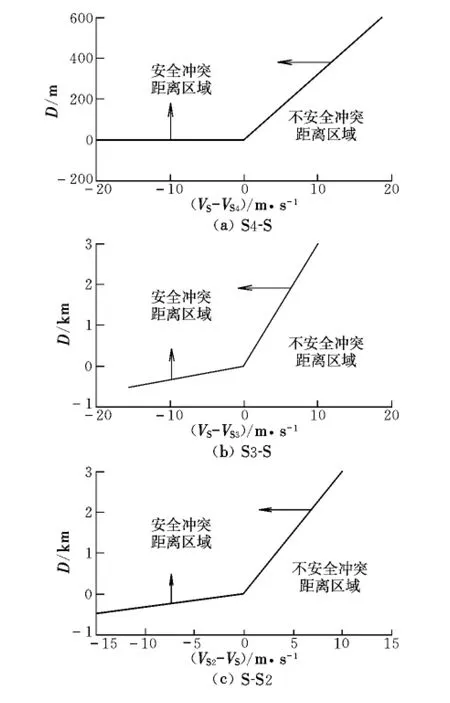
圖7 最小沖突距離區域Fig.7 Area of MCS

4 結束語

本文根據航空器之間的沖突距離，研究了航空器換道運動學的過程，并建立了平行航路的換道模型，得到航空器勻速飛行時與周圍相鄰航空器不會發生沖突的理論安全距離范圍。該范圍可為管制員進行管制工作提供理論依據，對研究空中高速路中航空器的運行問題也有一定的意義。

［1］ 中國民用航空管理局.2010年民航行業發展統計公報［EB/OL］.(2011-05-04)［2014-04-11］.http://www.caac.gov.cn/I1/K3/201105/t20110504-39489.html.

［2］ Hering H.Air traffic freeway system for Europe［J］.Euro Control Experimental Centre Technical Note，2005，3(5):29-36.

［3］ Hoffman R，Prete J.Principles of airspace tube design for dynamic air space configuration ［R］.AIAA-2008-8939，2008.

［4］ 王莉莉，劉兵.空中高速路網的設計討論［J］.系統工程，2012，30(11):107-111.

［5］ 王莉莉，張新瑜.空中高速路交通流的跟馳現象及流量模型［J］.西南交通大學學報，2012，47(1):158-162.

［6］ 沈金煒，張兆寧，劉計民.基于CNS定位誤差的平行航路間隔安全評估［J］.航空計算技術，2010，40(1):34-36.

［7］ 劉穎蕾.京滬平行航路的必要性和實用性探討［J］.空中交通管制，2011(6):6-8.

［8］ ICAO.確定最小間隔標準的空域規劃方法手冊［M］.國際民航組織文件，Doc 9689-AN/953，1998.

［9］ 劉兵.空中高速路網設計及其流量模型研究［D］.天津:中國民航大學，2012:48-50.

［10］王文霞.高速公路基本路段車輛換道安全距離模型的研究［D］.長春:吉林大學，2007:21.

［11］ Shladover SE，Desoer C A，Hedrick J K.Automatic vehicle control development in the PATH program［J］.IEEE Transactions on Vehicular Technology，1991，40(1):114-130.