提高數學教師創編試題和評價試題能力之我見
趙守文 毛遠鵬 楊俊杰 陳立維
(哈爾濱市龍滌新世紀學校哈爾濱市150010)
一、提高教師創編試題和評價試題能力勢在必行
新課程的實施,呼喚教師專業化發展。通過各學科組織的通識培訓和課程解讀,教師的專業化水平有了長足的發展。但是,隨著新課程不斷深入,如何使教師們對涉及到的教學環節的細微之處的學習、研究、交流諸方面達到科學的培訓和規范的要求,就將成為提高教師專業化水平的重中之重的工作。
鑒于目前教師在習題處理方面存在著三個弊端:一是搞題海戰術,盲目做題而不會評價和精選題目;二是照抄照搬各類復習資料和模擬題,而缺少自己的獨立思考,缺少自己的思想和主張的創編性題目;三是一套一套的做試卷,或簡單的對對答案或不了了之,缺少必要的反思和補救,訓練效果低。因此精選題目,編制題目,反饋矯正題目,評價題目,教做題目等既是檢驗學生所學的知識是否掌握的重要手段之一;又是應對多類評價和考試的重要渠道;還是教師教學的一項基本素質。是教師教學活動的一項重要的基本功,是校本教研重要內容。因而提高教師創編試題和評價試題能力勢在必行。
二、必須明確試題評價能力的范疇和探究試題創編的途徑
(一)試題評價能力的內容
1.基礎性及知識性:所謂基礎性是指通過填空、選擇或簡答等題型直接考查最基本的定義、性質、法則、詞匯、語句等。
2.綜合性及開放性:所謂綜合性就是指多個知識點的交匯,多種解題思想的融通,多種解題方法的應用,多個學科的整合;所謂開放性就是答案不是唯一的。條件或結論都是可以開放的。給學生張揚個性的空間。
3.生活性及實踐性:所謂生活性是指考查的問題同學生生活,社會生活,科技環境,當前時政方面緊密聯系;實踐性要求學生動手實驗、動手操作,如畫一畫、剪一剪、拼一拼、做一做等。
4.探究性及體驗性:所謂探究性就是通過觀察、探索、分析和歸納,得出相應的結論;體驗性,通過設計的參與的情境,使學生在活動過程中得到親身感悟和體會。
5.解法的多樣性及評估的多維性:是指一個題的解法過程的多種思路、多種方法。評估的多維性,是從教與學的多側面、多角度、多渠道的考查和應用。
6.區分性及層次性:一套試卷必須有層次,就是一道綜合試題也必須有層次。原則上體現出容易題、中檔題、較難題,這樣的檔次鋪設為學生構架了階梯,有利于對不同層次學生能力的考核。
(二)教師試題研究創編能力主要體現
1.創編題目的原型題資料(教材和各類資料的知識點或題目)
2.上述資料所賦予的背景或載體。
3.創編的意圖:知識內容的鏈接、延伸及擴展;條件及方法的演變及強化。
4.創編題目及答案。
5.創編題目的特點。
上述種種對教師的能力有了明確的表述,對培訓的內容做到了詳實具體,易于操作。
三、必須做到使提高教師創編試題和評價試題能力的培訓,可示范,可操作。
在明確了培訓的內容和程序之后,很重要一點是要使教師懂得如何去實施。
(一)試題評價舉例
題目:如圖,在坐標系中有矩形OABC。
(1)有一動點N以5cm/s的速度由O運動到A,再由A運動到B,的面積s與動點運動的時間t的函數圖像如圖1。請根據圖像求出矩形的邊長,并寫出s與t的函數關系式。
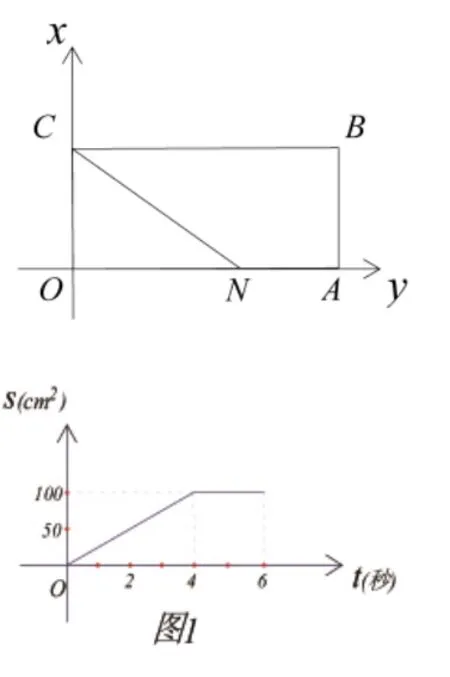
(2)若矩形的邊長如(1)中所求,動點Q以1cm/s的速度從點A出發,沿線段AO運動到O點(含O點),點Q出發5s后點P以2cm/s的速度由O點沿折線運動到點B(含點B)。當≌時,求點P的運動時間。

(2)①t=10;②t=15
評析:一是具有基礎性。無論是(1)中給出的一次函數圖像,還是(2)中的三角形全等都是最基礎的知識;二是具有探究性,(1)中的圖像觀察需根據三角形面積不變判斷點是在AB上運動,三角形的底邊和高都是定值。(2)中的三角形的判定需要猜想全等時的條件;具有很好的探究趨勢;三是綜合性。(1)題中圖像逆用及分段函數與(2)中的三角形全等的判定將幾何、函數等知識融為一體。四是區分性及層次性。本題各問體現了基礎性、銜接性和提升性三個不同檔次,這有利于不同層次學生能力的考核。
這里應該著重說明一點,在試題評價過程當中要做到有的放矢,實事求是,評價的要恰如其分。
<范例二>試題創編能力舉例
(二)創編過程
1.創編的原型題.原題是人教版數學教材第126頁11題:電信部門要修建一座電視信號發射塔。如圖,按照設計要求,發射塔到兩個城鎮A、B的距離必須相等,到兩條高速公路m和n的距離也必須相等。發射塔應建在什么位置上?在圖中標出他的位置。
知識內容是角平分線的性質和線段垂直平分線性質,而且是個實際應用作圖題。
2.創編的背景和載體。把原型題這一材料作為背景和載體,在此基礎上進行創編。
3.創編的意圖。原知識點關于角平分線和線段垂直平分線的性質保持不變,使其與直角坐標系及一次函數鏈接起來,使知識得到延伸及擴展;條件和方法的演變及強化:將其條件融于一個直角三角形中,且給出30°的特殊角,并增設直角三角形的一條直角邊與x軸正方向成30°角這一條件,這里又包含兩種情況,即30°和60°銳角與x軸正方向成30°角的問題。
(三)創編題目及答案
創編題目:有一個直角三角形,其一個銳角分別為30°,斜邊長為2。將它的一個銳角的頂點與直角坐標系的原點重合(在第一象限內,含兩個坐標軸),此直角三角形的斜邊與x軸正方向成30°角。求到該直角三角形的斜邊和一條直角邊距離相等且到斜邊兩端點距離相等的點的坐標。
答案:略解:
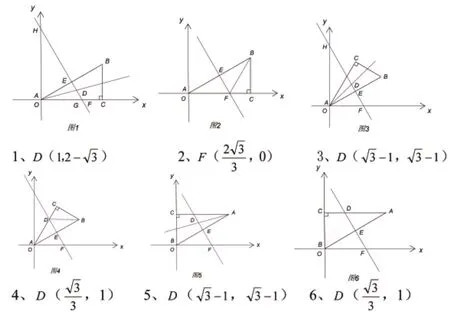
(四)創編題目的特點
1.知識的整體性。本題將平面幾何中的兩個重要知識點與函數和解直角三角形問題實現統一體。
2.答案的多樣性。由一條斜邊與x軸正方向成30°角這個條件就出現了三種可能,而每一種可能中又有兩種情況,因此共六個解。
3.解法的多元性。本體可用三角形全等、解直角三角形、三角形相似、勾股定理等諸多方法去解。
4.編制的創新性。本題的編制是新穎的、獨特的,是創造性的工作,可以說是具有專利權的。
提高試題評價及試題編制能力,不是一朝一夕的事。不能設想模仿幾道題的評價與創編,能力就會有大幅度提升。而必須在入門之后,只有經過多次訓練,一招一式踏實推進,進行深思熟慮的反思,循序漸進,長期不懈的艱苦努力,才會使創新思維和創新能力得到有效提高。評價試題和創編試題能力是提高教學質量重要環節之一,必將在提高教學質量方面有所突破。

