單/雙基地雷達超低空探測研究?

(軍械工程學院電子與光學工程系,河北石家莊050003)

0 引言

近年來,隨著空戰裝備技術的發展和空襲戰術的改進,現代戰場上巡航導彈、武裝直升機等超低空(高度在10～300 m之間)目標越來越多。這些目標飛行高度低、航線隱蔽,在地球曲率和地形起伏的遮擋,以及強地雜波的掩蓋下非常難以被發現。超低空突防在實施對敵打擊時的優勢在近幾十年的多次戰爭中被廣泛應用,對戰場要地防空提出了新的考驗[1]。

雙基地雷達由于收發分置,在對低空目標探測時具有單基地雷達無法比擬的優點[2-3]。根據Babinet原理,目標的前向散射雷達截面積(Radar Cross Section,RCS)與目標的表面形狀和涂覆材料無關,而完全由入射場和目標的輪廓決定,當雙基地角到達180°時,目標的RCS達到最大值。因此,雙基地雷達對低空目標的探測優勢主要是利用目標的前向散射區。然而,隨著雙基地角的增大,目標的距離估計精度會迅速降低,當雙基地角接近180°時,雙基地雷達基本喪失對目標的定位能力,可以認為是無效的探測區域。文獻[4-5]分析了雙基地雷達對金屬橢球體的低空探測能力。文獻[6]基于經驗公式分析了雙基地雷達對隱身目標的探測范圍。文獻[7-9]對臨近空間雙基地雷達的探測范圍進行了分析,這種配置下超低空區域的雙基地角相對較小,不利于對超低空目標的探測,同時在臨近空間配置大功率的發射機會有極大的成本和被發現的概率。文獻[10-11]分別對壓制干擾下的空地雙基地雷達探測范圍和基于旋翼無人機的空地雙基地雷達的空間同步進行了研究。以上文獻均沒有考慮雙基地角臨近180°時的無效探測區域,雙基地低空探測分析并不完善。

本文仿真分析了距離探測精度隨雙基地角的變化關系,綜合考慮了雙基地角臨近180°的無效探測區域,以及目標位于不同雙基地角下的RCS等因素,對單基地雷達、地基雙基地雷達和空地雙基地雷達在超低空區域對巡航導彈等弱目標的探測能力進行了對比分析。結果表明,地基雙基地雷達的探測盲區主要分布在超低空區域,而空地雙基地雷達將探測盲區轉移到了低空和中低空區域,對超低空弱目標的探測能力遠大于單基地雷達和地基雙基地雷達,用空地雙基地雷達作為現役單基地雷達的超低空補盲雷達有極大的應用價值。

1 單/雙基地雷達探測范圍分析

1.1 單基地雷達探測范圍分析

在不考慮方向圖傳播因子的情況下,單基地雷達方程為

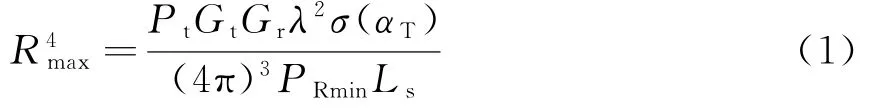
式中:Gt為發射天線增益,Gr為接收天線增益,對于單基地雷達,通常Gt=Gr;σ(αT)為與波束入射角相關的目標雷達截面積函數,αT為入射波束與水平面的夾角;Ls為損耗因子,Ls＞1;Pt為發射的峰值功率;PRmin為接收的最小可檢測信號功率。

式中:M為脈沖積累個數,當使用單個脈沖回波進行檢測時M=1;Pcr為寬帶接收機的脈沖壓縮比,Pcr=Pw×Bn(即時寬帶寬積);k為玻耳茲曼常數,k=1.38×10-23J/K;T0為標準室溫,一般取290 K;Bn為接收機的噪聲帶寬,一般由中放決定。

由式(1)可得,不同距離下單基地雷達接收到的信號能量為

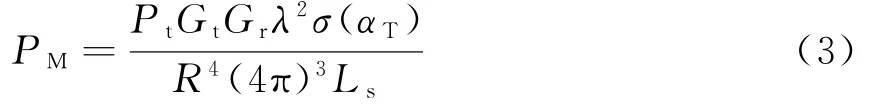
雷達若能發現目標,需要滿足

1.2 雙基地雷達探測范圍分析

在不考慮方向圖傳播因子的情況下,雙基地雷達的雷達方程不同于單基地雷達,為

式中,RT為目標到發射機的距離,RR為目標到接收機的距離,σB(β)為與雙基地角相關的目標雷達截面積函數,其他參數定義與單基地雷達方程相同。

由式(5)可得,不同雙基距離積下接收機收到的信號功率為

若雙基地雷達接收機的最小可檢測功率與單基地雷達相同,則雙基地雷達發現目標需滿足

為分析單/雙基地雷達在不同高度下的探測范圍,以單基地雷達為原點建立XOZ二維直角坐標。X軸表示地面,Z軸表示與地面的高度,對第一象限內的整個區域進行網格劃分,dx表示X軸的劃分間隔,dz表示Z軸劃分間隔,如圖1所示。

圖1 探測空域網格劃分

單基地雷達部署在(0,0)位置,則任意位置的目標(xi,zi)到雷達距離為

對于空地雙基地雷達,發射機部署在(H,0)位置,接收機部署在(L0,0)位置,基線距離L=,可得

分析單/雙基地雷達的探測范圍時,根據式(4)和式(7)計算圖1中劃分的每個網格中心點處的目標是否可以被檢測到。若能被檢測到,則認為整個網格內的區域均為可探測范圍,令發射機的高度H=0即可得到地基雙基地雷達的探測范圍。

2 目標的單/雙基地雷達截面積分析

進行超低空突防的目標主要為巡航導彈,為了便于分析,以細長金屬橢球體的RCS來近似替代巡航導彈的RCS,一般巡航導彈的尺寸遠大于雷達發射電磁波的波長,在不考慮表面涂覆材料的影響時,導彈的RCS一般處于光學區。橢球體處于不同位置時,其相對于雷達的視線角是變化的,記水平放置的橢球體的視線角與水平面的夾角為α,用標準物理光學近似法來分析細長金屬橢球體的單基地RCS如下[12]:

式中,a為橢球體的長軸長,b為短軸長。

文獻[6]通過分析得出了雙基地雷達截面積與單基地雷達截面積的經驗公式,為

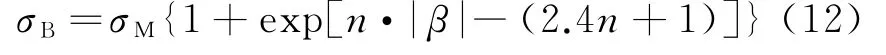
式中:σB為雙基地雷達截面積;σM為單基地雷達截面積;n為經驗參數,一般取7～10;β為雙基地角,單位為rad。

橢球體尺寸a=5 m,b=0.5 m,根據式(11)和式(12),圖2(a)給出了該橢球體不同入射角下的單基地RCS,圖2(b)給出了入射角為30°,n=8情況下,該橢球體不同雙基地角下的RCS。從圖2(b)可以看出,在雙基地角大于135°時,橢球體的RCS隨雙基地角的增大而迅速增加。

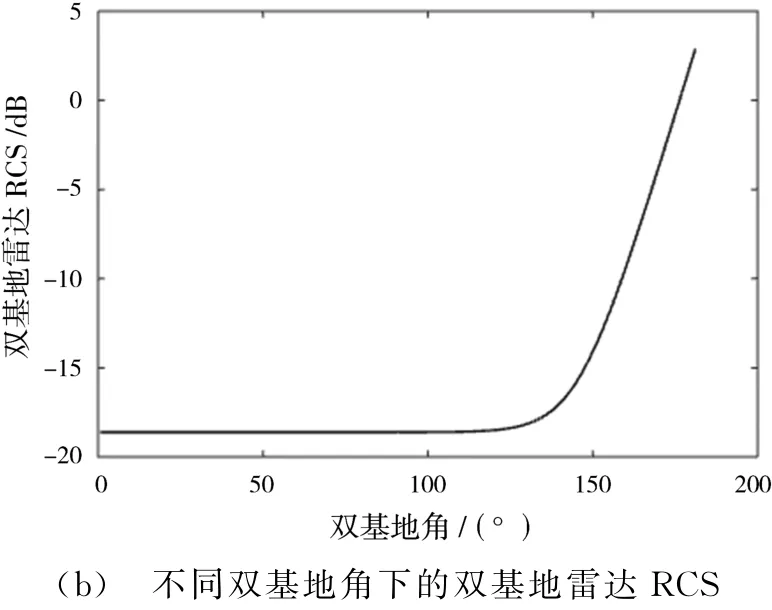
圖2 單/雙基地雷達RCS分布

3 距離探測精度分析

通常在雙基地平面中采用距離和-角度方法進行目標測距,得到接收站到目標距離RR表達式[13]為

式中,RS為發射站-目標-接收站距離和,L為發射站-接收站基線長,θR為雙基地平面上的目標視角。

在空地雙基地雷達中,如圖3所示,發射站的高度為H,其與接收站的傾角為θT,目標到發射站的距離為RT,目標到接收站的距離為RR,β為目標的雙基地角,RS,θR和L的定義同式(13)。

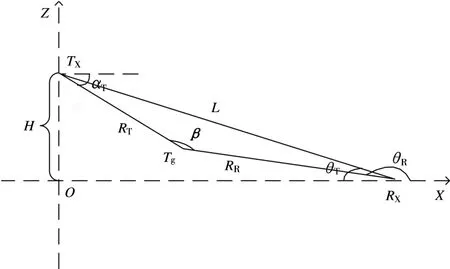
圖3 空地雙基地幾何示意圖

以接收站中心,將空地雙基地配置逆時針旋轉θT為地基雙基地配置,根據式(13),在空地雙基地雷達中,接收站到目標距離RR表達式為

目標的雙基地角

RR的測量誤差主要是由Rs,θR,θT和L的測量誤差導致的,根據誤差理論,均方根誤差表達式如式(16)所示:

4 仿真分析

仿真1:不同配置單/雙基地雷達對巡航導彈的低空探測范圍分析

以長軸長5 m、短軸長0.5 m的金屬橢球體目標為例進行分析,地基雙基地雷達的基線距離L=20 km,空地雙基地雷達發射機高度H=2 km,發射機和接收機的水平距離L=20 km。探測空域的網格劃分如圖2所示,dx=50 m,dz=5 m,整個空域范圍的水平距離為25 km,高度為1 000 m。不同配置的雷達發射天線增益和接收天線增益均為30 dB,損耗因子為10 d B,發射機功率為100 W,脈壓增益為10 dB,脈沖積累個數為10,接收機最小可檢測信號功率為10-13W。根據式(4)和式(7)得不同配置單/雙基地雷達對巡航導彈的探測范圍,如圖4所示。

從圖4可以看出,雙基地雷達(包括地基雙基地雷達和空地雙基地雷達)在對1 000 m以下的低空區域進行探測時有明顯的優勢,地基雙基地雷達對水平距離距發射機較近的區域有更強的探測能力,但在遠區低空區域,空地雙基地具有和地基雙基地雷達同樣強的探測能力。

圖4 不同配置下的單/雙基地雷達對巡航導彈的探測范圍

仿真2:雙基地雷達距離探測精度仿真分析

雙基地的距離探測精度與雙基地角之間的關系與雙基地配置無關,因此仿真采用的雙基地雷達配置同仿真1中的地基雙基地雷達,仿真時,根據式(17)和式(20)分別分析在距離和估計誤差和目標角度估計誤差影響下,雙基地雷達距離探測誤差斜率同雙基地角的變化關系,如圖5所示。圖5(a)的誤差斜率表示1 m的距離和測量誤差所產生的目標距離估計誤差,圖5(b)的誤差斜率表示0.1°的角度估計誤差所產生的目標距離估計誤差。

圖5 雙基地雷達距離探測精度與雙基地角的關系

基線測量精度、距離和測量精度對雙基地距離探測精度的影響是在同一數量級的且誤差斜率同雙基地角的變化趨勢一致,因此只需分析其中一個即可。圖5(a)和圖5(b)表明,當雙基地角大于174°時,距離和誤差和角度估計誤差對雙基地雷達的測距誤差影響成指數型增長;當雙基地角大于174°時,雙基地雷達幾乎失去對目標的距離測量能力。因此,雙基地角大于174°的區域可以認為是無效的探測區域。

仿真3:不同配置單/雙基地雷達有效探測區域仿真分析

根據仿真2分析,雙基地雷達的有效探測區域應為雙基地角小于174°的區域且在雙基地雷達的視距范圍內。單/雙基地雷達的配置方式同仿真1,根據式(15)計算這兩種雙基地配置對應的雙基地角等值線,如圖6所示。圖7在仿真2基礎上考慮了雙基地雷達的探測盲區,給出了不同配置的單/雙基地雷達在300 m以下超低空區域的有效探測范圍。

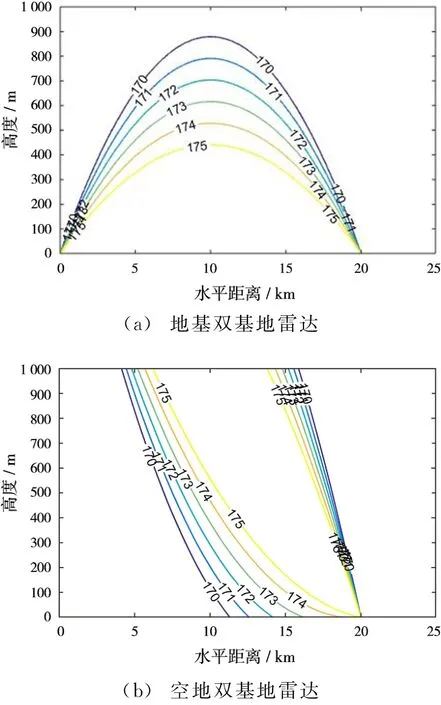
圖6 雙基地雷達等雙基地角曲線分布

圖7 不同配置單/雙基地雷達有效探測區域

從圖7可以看出,在相同的功率和收發天線增益條件下單基地雷達對巡航導彈的低空探測距離相對較近,普通的地基雙基地雷達對300 m以下的超低空區域存在極大的盲區,在此區域內普通雙基地雷達基本無法確定目標的具體位置,空地雙基地雷達隨著空域高度的降低有效的探測區域越來越大,因此對采用地形匹配制導的巡航導彈具有更強的探測能力。從單基地雷達和空地雙基地雷達的有效探測區域來看,在接近發射機的距離空地雙基地雷達存在盲區,而單基地雷達在這一區域內有較好的探測能力,因此空地雙基地雷達可以作為普通單基地雷達的超低空補盲雷達,從而增大對巡航導彈等進行超低空突防目標的探測能力。

5 結束語

理論分析和仿真結果表明,弱目標在大雙基地角下RCS會顯著升高,雙基地雷達對低空區域弱目標的探測能力要明顯強于單基地雷達,然而當雙基地角接近180°時,目標的距離探測精度會迅速降低。對比單基地雷達、地基雙基地雷達和空地雙基地雷達的有效探測區可以發現,空地雙基地雷達對于低空、超低空區域探測有著普通雷達難以比擬的優勢。空地雙基地雷達發射平臺具有較好的機動性,可根據戰場需求靈活地調整空地雙基地配置,從而使空地雙基地雷達發揮更大的作用,下一步將對不同配置下的空地雙基地雷達對超低空區域的探測范圍進行研究。

[1]馬井軍,馬維軍,趙明波,等.低空/超低空突防及其雷達對抗措施[J].國防科技,2011(3):26-35.

[2]楊振起,張永順,駱永軍.雙(多)基地雷達系統[M].北京:國防工業出版社,1998.

[3]李曉東.連續波擴頻雙/多基地雷達[J].電光系統,2000,92(2):35-39.

[4]張小寬,甄蜀春,鈔剛.單/雙基地雷達的低空探測性能研究[J].系統工程與電子技術,2003,25(12):1478-1480.

ZHANG Xiaokuan,ZHEN Shuchun,CHAO Gang.Research on the Low-Altitude Detection Performance of Monostatic and Bistatic Radars[J].Systems Engineering and Electronics,2003,25(12):1478-1480.(in Chinese)

[5]張小寬,甄蜀春,于慶國.雙基地雷達的探測范圍分析[J].彈箭與制導學報,2003,23(1):196-198.

[6]吳小坡,時家明,莫正攀,等.雙基地雷達對隱身目標探測區域的計算[J].現代防御技術,2012,40(4):124-127.

[7]門向生,田新華,宮健.臨近空間雙基雷達探測隱身目標性能研究[J].電光與控制,2009,16(5):43-46.

[8]陳長興,王博,牛德志,等.臨近空間雙基地雷達抗低空突防能力分析[J].現代電子技術,2011,34(23):1-3.

[9]王博,陳長興,牛德智,等.臨近空間雙基地雷達探測性能分析[J].實驗室研究與探索,2013,32(4):67-70.

[10]劉琪,孫仲康.空地雙基地系統的探測范圍分析[J].國防科技大學學報,1997,19(5):14-17.

[11]馬彥恒,宋瑤,董健.空地雙基地雷達空間同步研究[J].雷達科學與技術,2015,13(1):65-69.

MA Yanheng,SONG Yao,DONG Jian.Research on Spatial Synchronization in Air-Ground Bistatic Radar[J].Radar Science and Technology,2015,13(1):65-69.(in Chinese)

[12]郭文彥,呂長榮,張敬東.細長橢球導體雷達散射截面的分析計算[J].哈爾濱工業大學學報,1990(5):37-40.

[13]寧晉煒.雙基地雷達定位精度和空間同步方法研究[D].西安:西安電子科技大學,2011.