Winkler彈性地基板梁的自由振動分析①

Winkler彈性地基板梁的自由振動分析①

通信作者：蔣吉清。E-mail：jiangjq@zucc.edu.cn。

魏綱1， 李鋼2， 蔣吉清1， 魏新江1

(1.浙江大學城市學院工程分院，浙江 杭州 310015； 2.浙江大學建筑工程學院，浙江 杭州 310058)

摘要：中短型軌道板的幾何構型介于梁、板之間，屬于寬梁結構。從Mindlin板理論出發，退化得到適用于寬梁的Mindlin板梁控制方程；引入Winkler地基剛度系數，推導得到位移和轉角的模態函數表達式。考慮兩端簡支的邊界條件，得到彈性地基板梁的自由振動特征方程。通過無量綱數值算例求解出彈性地基板梁的自振頻率，并與Timoshenko梁理論和Mindlin板理論進行對比。研究高跨比、泊松比和彈性地基剛度等參數對結構自振特性的影響，總結出彈性地基板梁方程的特點及適用范圍，即寬度效應顯著且泊松比較大的寬梁結構。

關鍵詞：Winkler地基； Mindlin板梁； 自振頻率； 泊松比

收稿日期：①2014-08-20

基金項目：國家自然科學基金(51278463，11202186)；浙江省自然科學基金(LQ12E08009)

作者簡介：魏綱(1977-)，男，博士，教授，主要從事軟土地基處理和地下隧道結構相關的教學和科研。E-mail：weig@zucc.edu.cn。

中圖分類號:TU311.3文獻標志碼：A

DOI:10.3969/j.issn.1000-0844.2015.03.0655

Free Vibration Analysis of a Mindlin Plate-beam

on a Winkler Elastic Foundation

WEI Gang1, LI Gang2, JIANG Ji-qing1, WEI Xin-jiang1

(1.SchoolofEngineering,ZhejiangUniversityCityCollege,Hangzhou310015,Zhejiang，China;

2.CollegeofCivilEngineeringandArchitecture,ZhejiangUniversity,Hangzhou310058,Zhejiang，China)

Abstract：In recent years, short- and medium-length floating-slab tracks have become commonly used in railway engineering. These tracks are of a model type between a Winkler foundation beam and a Winkler foundation plate. For this type of wide-beam structure, a more suitable theory is required that both ensures calculation accuracy, as does the plate theory but also provides a simple analytical process, such as that of beam equations. In this study, the governing equations of the Mindlin plate are degraded and the dynamic equations for wide-beam structures are obtained: this is called the Mindlin plate-beam theory. Although the equations of the Mindlin plate-beam theory appear similar to the equations of the Timoshenko beam theory, the coefficient of bending stiffness is different and retains the direct influence of the Poisson's ratio parameters. This means that lateral deformation can be considered in the Mindlin plate-beam theory. The stiffness of the elastic foundation is also considered, and the equations are extended accordingly. For general analysis, the variables and parameters in this study are normalized and the expressions for both the vertical displacement and flexural rotation angle of a wide beam are obtained. Based on the boundary conditions, the dynamic characteristic equation for a simply supported wide beam is finally derived, and the normalized frequencies for the wide beam can be calculated through certain root searching programs. In this study, different kinds of boundary conditions are considered using the same procedure. To illustrate the wide-beam theory described herein, several numerical examples are used and the natural frequencies of a Mindlin plate-beam on a Winkler elastic foundation are compared with the results of a Timoshenko elastic foundation beam and a Mindlin elastic foundation plate. The results demonstrate the accuracy of the present equations. The effects of the height-to-length Poisson's ratios and elastic foundation stiffness are considered and the following conclusions are obtained from the numerical results: (1) For a simply supported wide beam, the first three frequencies of the plate-beam model show good agreement with those based on the Mindlin plate model. The discrepancy of the results from the two beam models increases with the width of the beam as compared to those of the Mindlin plate. However, the fundamental frequency of the Mindlin plate-beam theory still remains in good agreement with the plate theory; (2) the natural frequencies obtained from the Mindlin plate and Mindlin plate-beam theories will increase with the Poisson's ratio for a wide beam on an elastic foundation and those obtained from the Timoshenko beam theory will decrease. This result means that the relative error of the beam-plate and Mindlin plate will further reduce for a larger Poisson's ratio; and (3) the equations derived here are suitable for wide-beam analysis, can incorporate the effect of beam width, and are especially suitable for a wide foundation beam with a relatively large Poisson's ratio. The numerical examples based on this approximation theory are in good agreement with the Mindlin plate theory, while the equations and calculation process are much simpler.

Key words： Winkler foundation; Mindlin plate-beam; natural frequency; Poisson's ratio

0引言

梁和板是土木工程常用的結構形式，其相關的力學問題一直是學者研究的熱點[1-3]。工程中常用的梁理論有Euler梁和Timoshenko梁兩類，板理論則有Kirchhoff板和Mindlin板等。相對而言，Timoshenko梁和Mindlin板在中厚結構及中高頻動力分析方面更具優越性。有學者采用Timoshenko梁對Mindlin板進行退化分析[4]，但在退化過程中卻未能考慮Timoshenko梁在結構寬度方向上的尺寸效應。

彈性地基上的梁和板振動是工程領域廣泛關注的重要問題之一。呂朝鋒[5]基于二維平面理論和狀態空間微積分法分析了Winkler彈性地基梁的自由振動。Wang等[6]采用Green函數給出了彈性地基Timoshenko梁在不同參數條件下的靜動力解析解。Akhavan等[7]推導出了面內受荷時的Mindlin板在Winkler地基上的精確解。Xiang[8]分析了Mindlin板在分段不均勻彈性地基上的振動。

現在鐵路工程上常用的板式軌道，尤其是彈性CA砂漿板式軌道[9]和橡膠墊浮置板軌道[10]，其構件模型介于Winkler地基梁和Winkler地基板之間。對于這種寬梁結構，當前的研究大多集中在工程應用的角度，少有理論方面的討論。有必要尋求一種合適的計算理論，既能得到類似于板理論的計算精度，又能保證其分析過程如梁方程般簡潔。為此，Mindlin本人從Mindlin板的控制方程出發，退化得到適用于寬梁結構的動力方程[13]。本文將此退化方程整理并定義為Mindlin板梁方程(Mindlin Plate-beam theory，簡稱P-B方程)，并在方程中考慮彈性地基剛度的影響；通過數值算例分析Winkler地基上的Mindlin板梁的固有頻率，分別與Timoshenko彈性地基梁、Mindlin彈性地基板的計算結果進行對比，由此驗證本文方程。

1Mindlin彈性地基板梁的動力方程

根據Mindlin板的動力控制方程[10]，并假設轉角ψx和豎向撓度υ沿z方向保持不變，即ψx=ψx(x,t)，υ=υ(x,t)；同時，忽略繞y軸轉角ψz的影響，即可退化得到如下方程[12]

式中：E和G分別為彈性模量和剪切模量；ρ為材料密度;κ=π2/12為剪切系數;I是關于z軸的轉動慣量；A為橫截面面積；b為截面寬度;q為分布荷載；D=Eh3/12(1-μ2),為抗彎剛度系數；h為板厚;μ為泊松比。位移υ和轉角ψx的正方向如圖1所示。

圖1　板梁模型示意圖 Fig.1　Sketch of the plate-beam model

式(1)為適用于寬梁結構的Mindlin板梁方程，由Mindlin本人首先提出,該方程與Timoshenko梁方程非常相近，但抗彎剛度系數有所區別，并保留了泊松比參數的直接影響，若考慮彈性地基的影響，式(1)將變為

式中：Kw為Winkler地基剛度。

2彈性地基板梁的自由振動分析

對于單根均勻彈性地基板梁，當不考慮外力作用，即q(x,t)=0時，板梁處于自由振動狀態。根據分離變量法的思路，分別令υ(x,t)=V(x)eiωt，ψx(x,t)= ψ(x)eiωt，代入式(2)并消去eiωt可得

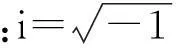
對于兩端簡支的彈性地基板梁，無量綱后的邊界條件可整理為：

將式(6)和(7)代入，并整理成矩陣形式：

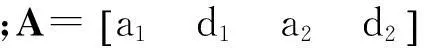
3數值算例及分析

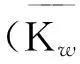
表1給出了不同地基剛度下三種計算理論得到的前三階無量綱頻率系數?。從中可以看到，不論是高跨比很小的淺梁(λ=1/100)、高跨比較大的深梁(λ=1/10)，還是更極端的矩形中厚板(λ=3/10)，板梁理論的結果總體上更接近二維Mindlin中厚板理論。

表1說明，在淺梁范疇(λ=1/100)，也就是長度方向的尺寸遠大于寬度和厚度時，雖然板梁理論的結果與Mindlin板理論更為接近，但Timoshenko梁理論與Mindlin板的最大誤差也僅為0.73%，且隨著地基剛度的增加誤差還在進一步降低。可見，在高跨比很小的淺梁范疇，采用Timoshenko梁理論，甚至是經典梁理論，都是可行的。

對于λ=1/10的深扁平梁，相比較Timoshenko梁的計算結果，板梁與Mindlin板理論更為接近。此時Timoshenko梁與Mindlin板的最大誤差增大近4倍，達到2.46%。隨著地基剛度的增加，誤差雖有所降低，但降低幅度不大。因此，對于較大高跨比的寬梁，板梁理論的計算結果相對于Timoshenko梁更接近實際，體現出板梁在寬扁梁到中厚單向板范圍內的優越性。

表 1　前三階固有頻率系數?的比較

針對λ=3/10且b/h=2的矩形中厚板，此時長寬高基本在一個量級范圍內。從計算結果看出:板梁理論得到的值與Mindlin板理論雖然更為接近，但也僅限于低階;在第三階時，兩種梁理論與Mindlin板理論的最大誤差都超過10%，隨著地基剛度的增加，誤差有所降低。因此，雙向矩形板范圍內板梁理論在低階頻率求解時能體現一定的優越性，但總體上看此時用梁理論來近似模擬已不合理。

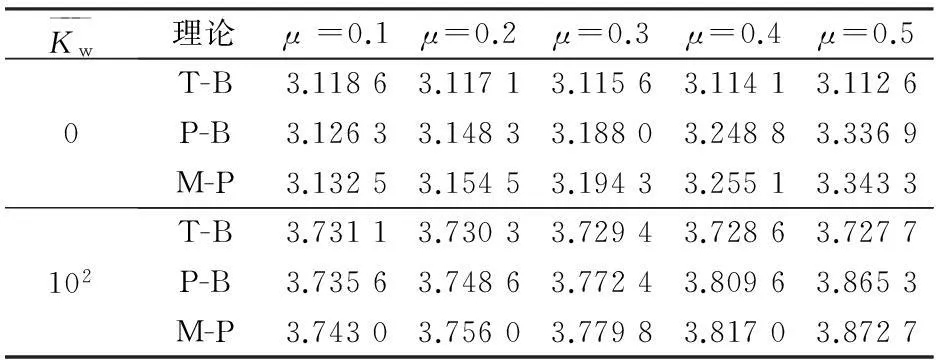
表 2　不同泊松比下三種理論的基頻系數比較( λ=1/10)

除了考慮結構尺寸的影響，還考察了三類理論在不同泊松比取值下的首階頻率系數隨地基剛度的變化情況。該結果基于b/h=2且λ=1/10的深扁平梁模型，同時也是板梁最佳的適用范圍。如圖2所示，在不同地基剛度下，隨泊松比的增加板梁的基頻增高，體現出與Mindlin板相同的趨勢。但是Timoshenko梁的變化趨勢卻剛好相反，即隨泊松比的增加，固有頻率有小幅度的下降。由此可以得出，對于泊松比較大的材料，采用板梁理論分析彈性地基寬梁結構的動力性能更加精確，也再次反映出板梁理論能夠考慮寬度變形效應的影響。

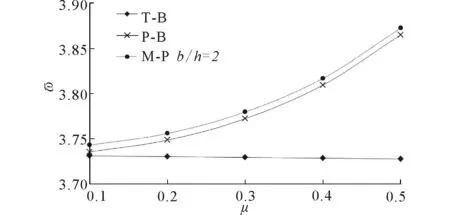
圖2　不同泊松比下三種理論基頻系數比較 　　　 ( ——=100) Fig.2　Comparison of the fundameratal frequency 　　　 coefficients based on three theories 　　　 with different Poisson’s ratios ( =100)

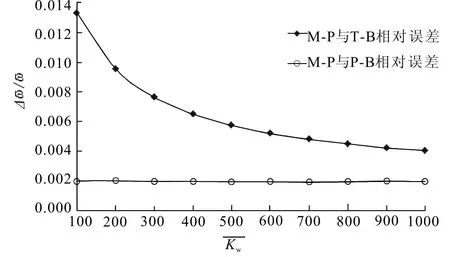
圖3　不同理論基頻隨地基剛度變化誤差 Fig.3　Comparison of the fundamental frequency 　　　 coefficients based on three theories 　　　 with different foundation stiffness

以Mindlin板為基準，分別考察不同地基剛度下板梁理論和Timoshenko梁理論的首階自振頻率系數相對誤差。如圖3所示，隨著地基剛度的增加，板梁與Mindlin板的相對誤差較為穩定，且相對較小;而Timoshenko梁與Mindlin板的相對誤差稍大，但隨著地基剛度的增加呈現減小的趨勢。

4結語

分析由Mindlin板理論退化得到的板梁控制方程在Winkler地基上的自振特性，得到以下結論：

(1) 簡支邊界條件下，在通常的中長梁范圍內，較之Timoshenko梁，彈性地基上的板梁與Mindlin板的前三階振動頻率更加吻合，且隨著板寬的增加，低階頻率同樣吻合良好。

(2) 隨泊松比的增加，彈性地基板梁的自振頻率趨勢及計算精度與Mindlin彈性地基板更加一致，當地基剛度增加時板梁與Mindlin板的相對誤差將進一步降低。

(3) 本文方程適用于寬度效應顯著(b/h≤4)、泊松比較大的Winkler地基寬扁梁結構，且在保證近似于Mindlin板理論的精度情況下，可以避免復雜的運算過程。

參考文獻(References)

[1]TimoshenkoSP.OntheCorrectionforShearoftheDifferentialEquationforTransverseVibrationsofPrismaticBars[J].PhilosophicalMagazine，1921，41(245)：744-746.

[2]TimoshenkoSP.VibrationProblemsinEngineering[M].NewYork:Wiley, 1974.

[3]ChakravertyS.VibrationofPlates[M].BocaRaton：CRCPress，2009.

[4]馬晨明.Kirchhoff板和Mindlin板上動態分布荷載的辨識問題研究[D].上海：復旦大學, 2004.

MAChen-ming.ResearchonDeterminationofDynamicLoadDistributionAppliedtoKirchhoffPlatesandMindlinPlates[D].Shanghai:FudanUniversity, 2004.(inChinese)

[5]呂朝鋒, 陳偉球, 邊祖光. 狀態空間微積分法分析Winkler地基梁的自由振動[J].浙江大學學報:工學版,2004, 38(11):1451-1454.,

LVChao-feng，CHENWei-qiu，BIANZu-guang.FreeVibrationAnalysisofBeamsonWinklerFoundationviaState-space-basedDifferentialQuadrature[J].JournalofZhejiangUniversity:EngineeringScience,2004，38(11)：1451-1454.(inChinese)

[6]WangCM，LamKY，HeXQ.ExactSolutionsforTimoshenkoBeamsonElasticFoundationsUsingGreen’sFunctions[J].MechanicsofStructureandMachines, 1998, 26(1)：101-113.

[7]AkhavanH，HosseiniHashemiSh，RokniDamavandiTaherH,etal.ExactSolutionsforRectangularMindlinPlatesUnderIn-planeLoadsRestingonPasternakElasticFoundation.PartII:FrequencyAnalysis[J].ComputationalMaterialsScience,2009,44：951-961.

[8]XiangY.VibrationofRectangularMindlinPlatesRestingonNon-homogenousElasticFoundations[J].InternationalJournalofMechanicalSciences，2003，45：1229-1244.

[9]左景奇，姜其斌，傅代正，等.板式軌道彈性墊層CA砂漿的研究[J].鐵道建筑，2005，9：96-98.

ZUOJing-qi，JIANGQi-bin，FUDai-zheng，etal.StudyofCementAsphaltMotarIncludedinElasticPadUnderSlabTrack[J].RailwayEngineering，2005，9：96-98.(inChinese)

[10]耿傳智, 樓夢麟. 浮置板軌道結構系統振動模態分析[J].同濟大學學報：自然科學版，2006，34(9)：1201-1205.

GENGChuan-zhi，LOUMeng-lin.VibrationModelAnalysisofFloatingSlabTrackSystem[J].JournalofTongjiUniversity：NaturalScience,2006, 34(9)：1201-1205.(inChinese)

[11]MindlinRD.InfluenceofRotatoryInertiaandShearonFlexuralMotionsofIsotropic，ElasticPlates[J].JournalofAppliedMechanics，1951，18(1)：31-38.

[12]MindlinRD.Thickness-shearandFlexuralVibrationsofCrystalPlates[J].JournalofAppliedPhysics，1951，22(2)：316-323.

[13]CalimFF，AkkurtFG.StaticandFreeVibrationAnalysisofStraightandCircularBeamsonElasticFoundation[J].MechanicsResearchCommunications, 2011, 38(2):89-94.