從實數不等式到矩陣不等式的演變

胡汭

（銅陵學院，安徽 銅陵 244061）

從實數不等式到矩陣不等式的演變

胡汭

（銅陵學院，安徽 銅陵 244061）

文章通過矩陣的相關知識，將兩個實數不等式演變到矩陣跡的不等式以及矩陣的范數不等式，并且得到該范數不等式的變形形式；在該方法中主要應用矩陣論中半正定Hermite矩陣、酉矩陣以及矩陣跡的相關知識得到兩個簡單的實數不等式的推廣形式。

實數不等式；矩陣的跡；范數；正定矩陣

眾所周知，不等式理論在矩陣理論中占有重要的地位，它滲透到數學的各個領域，當然隨著現代科學的發展，矩陣不等式理論已經在工業生產、經濟管理和交通運輸等多個領域都有著深入的滲透。隨著矩陣不等式理論的廣泛應用，科學家們不斷將矩陣理論知識轉化為科技成果。這些新成果不僅使得人們享受它帶來的財富和便利，更使得人們對矩陣理論知識有了新的和更深入的思考，并將矩陣理論劃分為更細的分枝。本文通過對矩陣理論知識的研究得到一種新方法，這種新方法是將兩個實數不等式演變到矩陣跡的不等式以及范數不等式，并給出了該范數不等式的推廣形式。這種方法就是本文要闡述的精髓。

1 預備知識

定義1 A＝（aij）為n階復方陣，稱它的對角元素之和為矩陣A的跡，稱為trA，即若 l1，l2，……，ln為A的特征值，則成立。[1]

定義2 A＝（aij）為n階復方陣，定義，則它是一個矩陣范數，稱它為Schatten p-范數.當p=2時，稱之為Hilbert-Schmite范數（或Frobenius范數），且知A*為A的共軛轉置。‖A‖2是酉不變范數，即對任意的酉矩陣U，V有‖UAV‖2=‖A‖2成立[1]。以下k，n均為正整數[1]。

引理1 對任意大于等于零的實數x，不等式x3+1≥x2+x都成立。

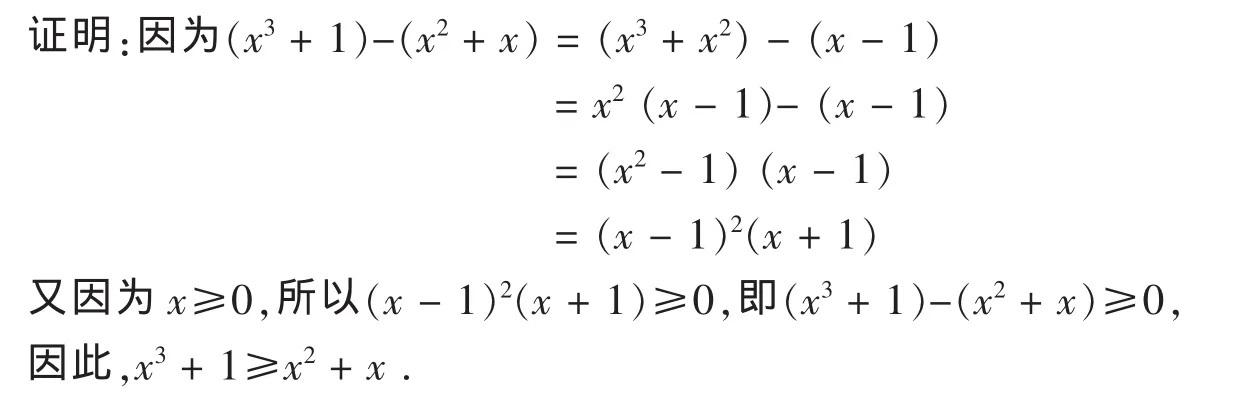
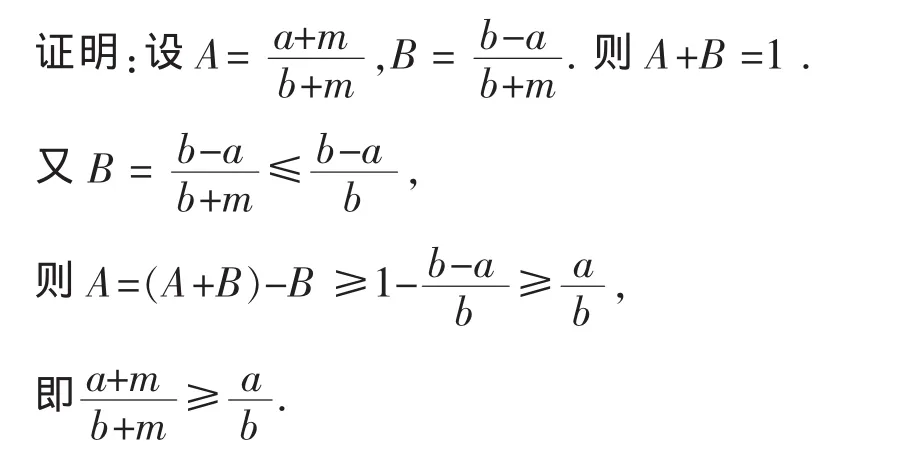
引理3 （Neumann）設A，B為兩個n階Hermite陣，它們的特征值分別為λ1≥λ2≥…≥λn和μ1≥μ2≥…≥μn則

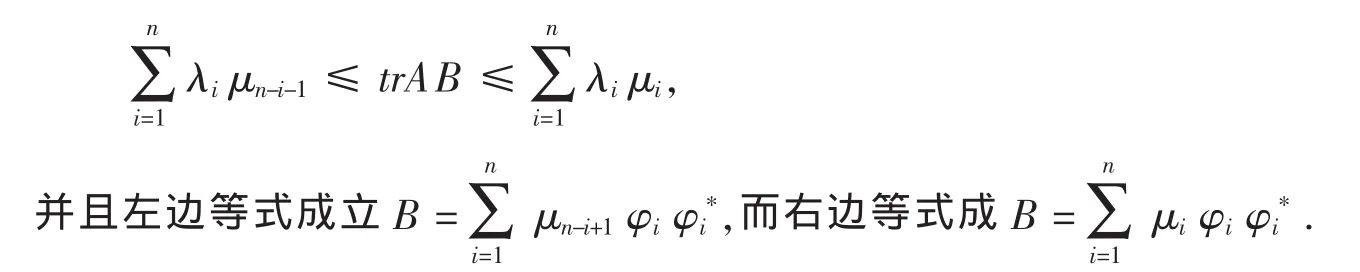
這里l1，l2，……，ln為A的對應于l1，l2，……，ln的標準正交化特征向量[1]。

2 主要結果

定理1 設A為n階半正定Hermite陣，則有tr（A3＋In）≥trA2+trA

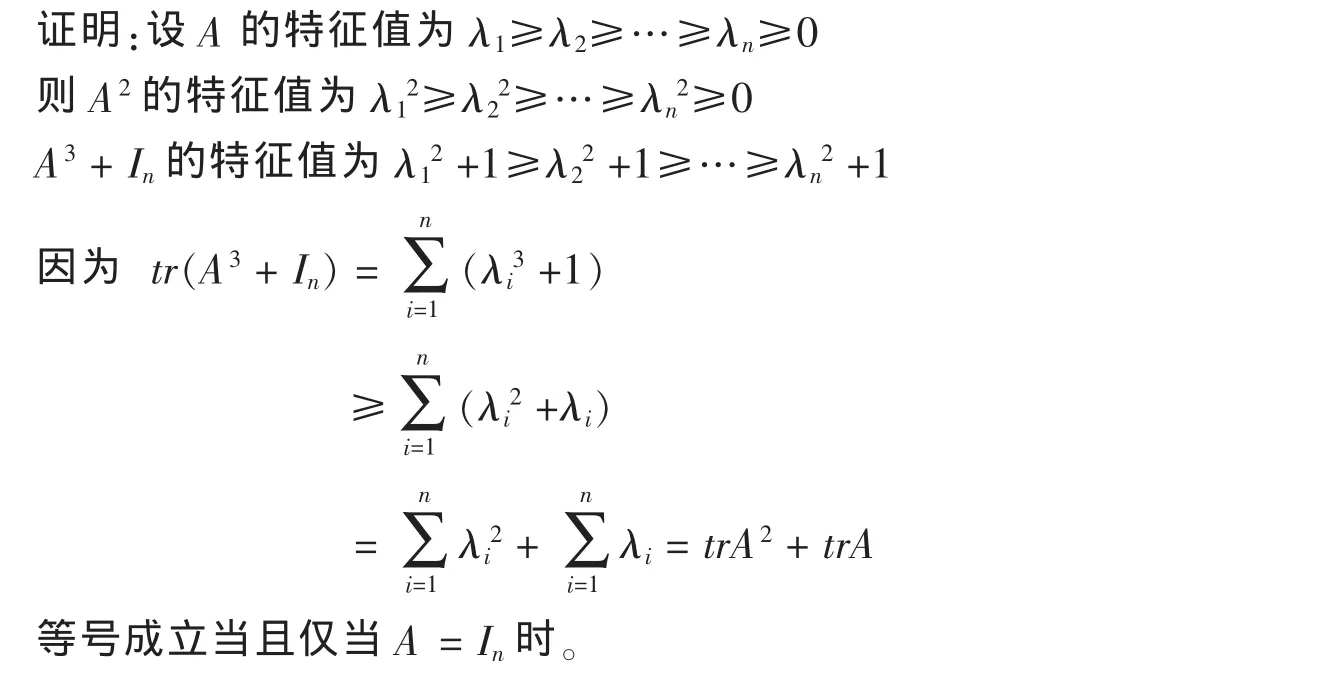
定理2 設A為n階半正定Hermite陣，則有

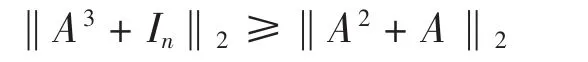
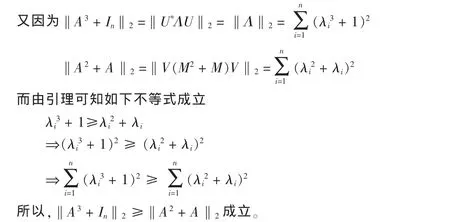
定理3 設A為n階半正定Hermite陣，X為任意n階復方陣，則有：

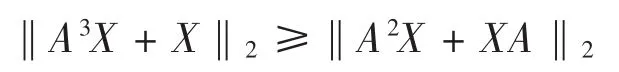
定理4 設X，A，B為同階半正定Hermite矩陣，且trB≥trA，trB≥0，則

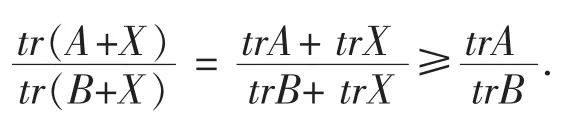
定理5 設A，B為n階半正定Hermite陣，且B≥A，X為任意n階方陣，則有

[1]王松桂，吳密霞，賈忠貞.矩陣不等式：第二版[M].北京：科學出版社，2006:4、18、139.

A STUDY ON THE EVOLUTIONS FROM THE REAL INEQUALITY TO THE MATRIX INEQUALITY

HU Rui
（Tongling University,Tongling Anhui 244000）

Two real inequality are evolved into the matrix trace inequality and norm of the matrix inequality in the paper through the knowledge of matrix.Therefore,the deformation form of the norm inequality is obtained.The positive semi-definite matrix of Hermite,unitary matrix and knowledge relevant to the trace of matrix are applied in the method to get the extension mode of two simple real inequality.

The real inequality；The trace of matrix；Norm；Positive definite matrix

O178

A

1672－2868（2016）06－0011－04

責任編輯：楊松水 校對：陳 侃

2016－08－28

胡汭（1985-），女，安徽六安人。銅陵學院數學與計算機學院，講師。研究方向：應用數學。