彈炮結合防空系統作戰部署建模與分析*

劉鴻福，翁郁，王志強

(國防科技大學 機電工程與自動化學院，湖南 長沙 410073 )

空天防御體系與武器

彈炮結合防空系統作戰部署建模與分析*

劉鴻福，翁郁，王志強

(國防科技大學 機電工程與自動化學院，湖南 長沙 410073 )

對彈炮結合防空系統部署的依據和方法進行研究，在線形、扇形和環形3種基本的部署模型基礎上，詳細分析了彈炮結合防空系統的殺傷區范圍及主要參數，并在此基礎上解算了殺傷區的特征值計算模型，利用任務規劃系統進行軟件仿真，驗證了模型的正確性。

任務規劃；彈炮結合防空系統；火力防區；兵力部署；火力分配原則；防御體系建模

0 引言

目前在低空、超低空防御體系中主要存在3種防空武器，一是防空導彈；二是自行高炮；三是彈炮結合防空武器系統。彈炮結合防空武器系統作為野戰和要地防空的重要武器裝備，同時也是末端防御的重要手段。

彈炮結合防空系統是近年來新興的防空武器系統，但發展和應用很快。現今各國都研制了不少彈炮結合武器系統。目前國外主要在以下2個方面大幅運用彈炮結合防空系統。一是作為末端防御的重要手段對巡航導彈的末端攻擊進行快速有效防御；二是作為高機動和高密集火力的重要防御手段伴隨裝甲部隊，對武裝直升機等高機動目標實施實時精確快速防御。

本文主要是針對彈炮結合防空系統防空進行分析研究，通過構建模型、研究戰術戰法，提出合理有效的作戰任務規劃方法。其研究有助于提升彈炮結合防空系統的作戰使用效能，有助于更加深入理解聯合作戰中各兵種的協同配合，為今后的作戰運用提供理論依據。

1 彈炮結合防空系統的殺傷區建模

1.1 火力防區劃分與建模

高炮射程較近、反應較快，一般都是針對近前目標進行作戰[1]，它的防空區主要由有效射程、有效射高、射程死角和最大射角4個因素確定[2]。防空導彈火力準備時間較長，單發毀傷概率高，一般都是針對中遠程目標進行作戰，它的防空區域主要由射程遠界、射程近界、作戰高界和低界確定[3]；同時，防空導彈還可以對過航目標進行攻擊，本文只分析過航前后射程遠界相同的情況。

根據不同距離下導彈和高炮的毀傷概率特點來看[4]，對于導彈而言，不同的殺傷近界對整體的毀傷效能影響不大，本文只討論殺傷近界為1 km的導彈；在殺傷近界之前存在作戰死區，從殺傷近界到正常工作區需要500～1 000 m的緩沖距離，這一段距離雖然有防空作戰的能力，但作戰效能不穩定，不作為導彈的火力防區。對于高炮而言，在最大有效射程附近的毀傷概率較低，對目標威脅性較小，所以此區域不作為高炮的火力防區。

在火力防區劃分時，需要給高炮留足完成一個長度為2 s的點射時間，也就是大概1.5 km。考慮到高炮為多發點射射擊，一個點射的總毀傷概率較大，所以可以將其火力防區適當擴大。為了保證更加明確地區分高炮和導彈的火力防區，避免火力分配混亂，火力重疊區不宜太大。

根據上述分析，確定以下建模原則：

(1) 高炮攻擊區從0距離開始，防區遠界的毀傷概率不能低于0.4；

(2) 導彈攻擊區的起始端要至少大于發射近界500 m；

(3) 導彈攻擊區的平均毀傷概率不能低于0.65；

(4) 火力重疊區范圍不宜超過1 km。

建立以下火力防區模型，并計算相關的平均毀傷概率：當斜距離小于1.5 km時，火力防區為高炮攻擊區，平均毀傷概率為0.62；當斜距離1.5～2 km時，火力防區為火力重疊區，平均毀傷概率為0.7；當斜距離大于2 km時，火力防區為導彈攻擊區，平均毀傷概率為0.68。

1.2 火力分配原則與建模

火力防區劃分完成之后，需要對各防區的火力進行分配，以達到最好的防御效果。對于彈炮結合防空系統而言，當目標處于高炮攻擊區內時，必須由高炮進行火力攻擊；當目標處于導彈攻擊區內時，必須由導彈實施火力打擊；當目標處于火力重疊區時，高炮和導彈皆能攻擊，為避免火力分配混亂，需要建立分配原則，并進行簡單建模[5]。

火力重疊區的火力分配需要解決的核心問題是在該區域內的目標用哪種武器打擊更有效。這要從2個方面考慮：一是彈炮結合防空系統本身作戰性能。導彈和高炮的單獨作戰方式有很大差別。導彈發射基本上不需要提前量，只要導彈瞄準鎖定目標就可以發射；而高炮射擊必須要在火控系統給出提前量、隨動系統調轉火力到目標未來點的情況下才能擊發[6]。另外，導彈的飛行速度快，具有自導跟蹤的能力，對于機動靈活的目標可以實施跟蹤打擊，并且單發毀傷概率較高[7]；而高炮初速慢，主要是依靠數量優勢產生的面殺傷達到攔截效果，炮彈自身沒有機動性，彈道比較單一，比較適合攔截航跡固定的飛行目標。二是來襲目標的特點。目標的飛行速度、機動過載能力、目標價值將很大程度上決定攔截方式的變化。

根據上述分析，確定以下火力分配原則：

(1) 高速度目標由導彈攔截；

(2) 低機動能力目標由高炮攔截；

(3) 低價值目標由高炮攔截。

在上述分配原則的基礎上以目標速度v、機動過載能力g和目標價值w為基本參數建模。目標權函數表示為

T=vα1+gα2+wα3,

(1)

式中：α1，α2和α3為權重系數，表示各參數的重要程度。

用層次分析法[8]對權重系數進行評估，通過兩兩比較，確定權重大小。假設專家評估結果為：機動過載能力相對于目標速度要重要，分數值為6∶5；目標速度相對目標價值要重要，分數值為7∶6。則通過計算可以得出α1=0.33，α2=0.39，α3=0.28。各參數的具體數值通過分段取值法可以進行量化，將量化值代入目標函數就可以求出目標函數值。目標函數值越大，越適合導彈攔截，目標函數值越小，越適合高炮攔截。

2 兵力部署模型的構建與效能分析

2.1 兵力部署模型

根據防空系統作戰的基本規律、基本原則，彈炮結合防空系統的兵力部署依據主要有以下4個方面：

一是保護目標的情況；二是敵方使用的兵力；兵器及采用的戰術技術手段；三是我方兵力的數量及裝備的作戰性能；四是保衛同一目標的友鄰部隊部署情況。

根據不同的實際情況，彈炮結合防空系統的部署模型是多種多樣的，但就基本模型而言，主要有線形部署、扇形部署和環形部署3種模型[9]。

線形部署是在敵方可能的主要來襲方向上，將防空兵力沿保衛區域呈一線配置。該部署方式能夠形成較大的攔截正面寬度，但火力縱深小，防線容易被破壞，一旦某一防御點被突破，剩余的防御力量將很難收縮支援。此防御方式適用于防御范圍較大的矩形防御區域，也適合背靠強大的后方保護或者天然地形屏障，以及敵方多航路、寬正面來襲等情況。

扇形部署是在我方兵力不夠充足的情況下使用，在防御區域的主要作戰方向上，將防御兵力以扇狀的方式配置。其突出優點是節約兵力，通過集中兵力，在主要作戰方向形成嚴密的火力防御網，抗擊能力強。但是這種部署方式的可靠性較差，如果敵方改變進攻方向，便會避開火力防區，造成重大失誤，風險較大。因此，扇形部署可以和環形部署搭配使用，外圈防御區在可能的主要作戰方向采用扇形部署，內圈防御區采用環形部署。

環形部署是在己方兵力比較充足，并且敵進攻方向不明確時使用，在保衛目標周圍以環形的方式部署兵力。環形部署具有很強的防御能力，能顧及到所有可能的作戰方向，具有全方位的抗擊能力，可靠性高。對于特別重要的目標，還可以采取多層環形部署，增大防御縱深，進一步提高防御的可靠性。但是其不足也很明顯，對于同一個保衛目標，其需要的兵力數量最多。

對于上述建立的3個部署模型，可以從2方面進行優化：一是在一定數量的火力單元的情況下，通過調整各火力單元之間的相對位置關系，盡可能地增大防御角和防御寬度；二是在滿足一定防御角和防御寬度的防御要求下，通過理論分析比較，選擇最優的部署模型，使得所需火力單元最少。

2.2 模型理論分析

在地面防空過程中，有兩種常規的防空方式，一是將投彈目標攔截在可投彈的最遠范圍之外，這一防空區域叫做投彈區[10]；二是將來襲的空中目標攔截在最大殺傷范圍之外，這一防空區域叫做安全區。本文以下涉及到的理論分析均是針對投彈區展開研究，安全區的防御模型分析可以類比于投彈區。

對于具有遠距離投彈的空中目標，盡可能多的將其攔截在投彈區之外能夠最大限度地減少空中目標的數量，大幅增強防空效能，減少空襲損失。

投彈區的計算公式如下：

RT=rm+rs+rt，

(2)

式中：RT為投彈區的半徑；rm為保衛目標的半徑；rs為空襲武器的毀傷半徑；rt為投彈目標水平投彈距離。

對于自殺式無人機、巡航導彈和彈道導彈等類似的不需要投彈的空襲兵器，其不具有投彈區，只能在安全區之外攔截[11]，因此，安全區的確定也至關重要。

安全區的計算公式如下：

RA=rm+rs，

(3)

式中：RA為安全區的半徑。

掩護角是指防御兵力能夠對保衛目標提供的防御角度，掩護寬度是指防御兵力能夠在正面對保衛目標形成橫向防御線的長度。這2個防御要素是評價防御系統優劣的重要指標，其中掩護角尤為重要。

在部署彈炮結合防空系統時，為了以最合理的方式、最少的兵力完成部署，需要對每一個火力單元的掩護角和掩護寬度進行計算，盡量減少火力重疊區[12]。圖1表示了火力單元對投彈目標的各攔截要素之間的關系。

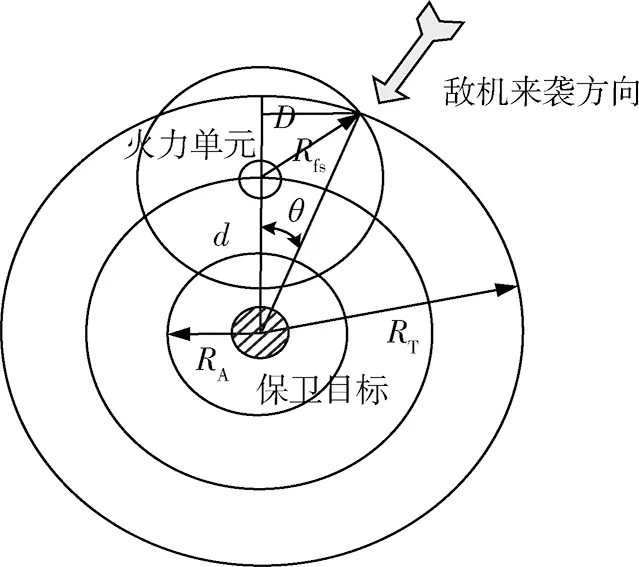
圖1 火力單位攔截要素示意圖Fig.1 Fire units to intercept features

圖1中，Rfs表示火力單元的殺傷遠界，d表示為火力單元部署點距保衛目標中心的距離，2θ表示為掩護角，2D表示為掩護寬度[13]。由圖中關系可知，計算掩護角和掩護寬度之前需要對d，RT，Rfs之間的大小關系進行比較。

當d≤Rfs-RT時，

2θ=360°; 2D=+∞.

(4)

2D=+∞表示投彈目標無法在保衛目標正面實施有效投彈。

當Rfs-RT

(5)

當d≥Rfs+RT時，

(6)

當彈炮結合防空系統以線形方式部署時，可計算其掩護寬度和掩護角[14]：

Lx=N2D;αx=arctanNtanθ,

(7)

式中:Lx為線形模型的掩護寬度;αx為線形模型的掩護角;N為火力單元的個數。

當彈炮結合防空系統以扇形方式部署時，可計算其掩護寬度和掩護角：

(8)

式中：αs為扇形模型的掩護角；Ls為扇形模型的掩護寬度。

當彈炮結合防空系統以環形方式部署時，可計算其掩護寬度和掩護角：

Lh=+∞;αh=360°，

(10)

式中：Lh為環形模型的掩護寬度；αh為環形模型的掩護角。

對于不同的兵力部署模型，其防御要求的不同會影響所需火力單元的總數。

線形部署以防御寬度作為防御要求，若所需防御寬度為L，則所需火力單元總數：

(11)

式中：[ ]為取整符號。

扇形部署以防御角作為防御要求，若所需防御角為α，則所需火力單元總數：

(12)

環形部署以防御區域半徑作為防御要求，若所需防御半徑為R(R≥RT)，將式(4),(5)中的RT用R代替，則可以得到所需火力單元總數：

(13)

彈炮結合防空系統火力單元的相對位置因部署方式的不同而有所區別。

如果采用線形部署的方式，其火力單元之間的部署距離dx為

dx=2D，

(14)

式中：2D為火力單元掩護寬度，具體計算見式(5)和式(6)。

如果采用扇形部署的方式，當被掩護目標為大面積掩護對象時，火力單元與被掩護對象的距離則較大，式(14)仍基本適用。由于環形部署與扇形部署類似，所以，其火力單元之間的相對位置仍然可以采用式(14)。

3 實驗與分析

利用任務規劃軟件[15]，對于第2節中建立的模型通過實驗仿真進行驗證。

根據第2節掩護角和掩護寬度計算模型可以分別計算出達到最大防御角和防御寬度時部署點距離保衛目標中心的距離。當以線形方式部署時，最優部署距離為17.3 km，掩護角為81.8°，掩護寬度為76.7 km，火力單元之間的間隔為19.2 km；當以扇形部署時，最優部署距離為17.3 km，掩護寬度為34.6 km，火力單元之間的間隔為17.3 km；當以環形部署時，最優距離為17.3 km，火力單元之間的間隔為17.3 km。

在仿真軟件中將兵力按照上述計算結果進行部署，圖2、圖3和圖4分別為線性部署、扇形部署和環形部署的仿真結果，從圖中可以看出，優化部署的3種模型將所有的空中目標全部擊落，達到了良好的防御效果。

圖2 線性部署Fig.2 Linear deployment

圖3 扇性部署Fig.3 Fan deployment

圖4 環性部署Fig.4 Ring deployment

為了使實驗結果更加可靠，基于上述作戰任務想定，對扇形模型做了多次對比實驗，將對比實驗的結果進行統計比較。統計比較結果如表1所示。

表1 對比實驗統計表Table 1 Comparative experimental statistics

當部署距離過近時，由式(5)和式(9)可計算得到的掩護角αs和掩護寬度Ls很小，火力單元在最遠投彈區域附近的火力密度不夠，以致敵機可以輕易躲避攻擊，并且有機會發射空地導彈摧毀目標，沒有達到防御的要求。

當部署距離較近時，部署的彈炮結合防空系統能夠保衛好目標，盡管其可提供的掩護寬度Ls相對最優方案有一點點優勢，但其可提供的掩護角αs和毀傷敵方目標的距離相對最優方案差距很明顯。

當部署距離大于最優距離時，也能夠保衛好目標，其可提供的掩護寬度Ls和毀傷敵方目標的距離已達到極限，并不隨部署距離的大幅增加而有明顯提高，基本上不影響防御體系的防御效果。而且其最重要的防御指標掩護角αs卻有較明顯的減小，對整個防御體系影響較大。相當于大幅度犧牲重要指標來小幅度提高次要指標，這不符合實際防御效能要求。

綜上分析可知，此模型得出的最優距離是合理且正確的。

4 結束語

本文先是以單個彈炮結合防空系統為基礎研究導彈和高炮的防區劃分與火力分配問題，構建了防區劃分模型，提出了火力分配原則。然后基于線形、扇形和環形3種最基本的防空部署模型，從掩護角、掩護寬度、兵力需求和火力單元之間的相對位置四個方面對3個部署模型構建了詳細的計算模型，并通過仿真實驗驗證了計算模型的正確性，可以為彈炮結合防空系統的兵力部署提供有效的決策依據。

盡管論文對3個部署模型進行了詳細的分析研究，但是由于武器裝備本身的火力射擊與毀傷能力難以量化，影響戰場態勢變化的因素較多，并且往往具有不可預測性，這使得論文中構建的理論計算模型與理論分析存在一定的不足，有待進一步研究與優化。

本課題涉及到的彈炮結合防空系統是一種比較新型的防空作戰武器，其作戰能力不能忽視，在實驗中發現，彈炮結合戰車中的防空導彈的速度、毀傷概率和裝填時間對整個系統的毀傷能力有很大影響。因此彈炮結合防空系統中使用的近程防空導彈可比以往超高速方向發展，縮短反應時間，提高單發導彈的命中概率。

[1] 石磊.彈炮結合武器系統作戰效能評估方法[D].北京：中國航天科工集團第二研究院，2006. SHI Lei.Research on Evaluation Method of Combat Effectiveness of Missile-Gun Combal Weapon System[D].Beijing:The Second Research Academy of CASIC,2006.

[2] 王鳳山，李孝軍，馬栓柱.現代防空學[M].北京：航空工業出版社,2008. WANG Feng-shan, LI Xiao-jun, MA Shuan-zhu. Modern Air Defense Technology[M].Beijing: Aviation Industry Press,2008.

[3] 王克強.防空概論[M].北京：國防工業出版社,2012. WANG Ke-qiang. Antiaircraft Introduction[M]. Beijing: National Defense Industry Press, 2012.

[4] 馬春茂，陳熙，侯凱，等.彈炮結合防空武器系統總體設計[M].北京：國防工業出版社,2008. MA Chun-mao, CHEN Xi, HOU Kai,et al. Missile-Gun Integrated Air Defense Weapon System Design[M]. Beijing: National Defense Industry Press,2008.

[5] LI D F. Fuzzy Multi Objective Many-Person Decision Makings and Games[M].Beijing National Defense Industry Press,2003,1：138-158.

[6] Grey Hawk. Cooperative Engagement Capability(CEC)[C]∥U.S.Washington D.C.: Network-Centric Air Defense, 2001,6.

[7] CHIANG J T.Defense Conversion and Systems Architecture: Challenges to Taiwan’s Aircraft Industry [J]. Technology in Society, 1999,21(3):263-274.

[8] 馮璐，高曉光. 層次分析法在多目標攻擊邏輯與決策中的應用[J].西北工業大學學報,1998，17(4)：515-519. FENG Lu, GAO Xiao-guang. Application of Analytic Hierarchy Process in Multi-Objective Attack Logic and Decision Making.[J]. Journal of Northwestem Polytechnical University, 1998, 17(4): 515-519.

[9] 吳家明.地面防空武器系統混合部署方法研究[D].長沙: 國防科學技術大學，2009. WU Jia-ming. Study on Derivative-Free Algorithms in the Air-to-Sea Single Observer Passive Tracking Application [D]. Changsha: National University of Defence Technology, 2009.

[10] 王君，陸小平，婁壽春.防空作戰運籌中的敵情、我情分析模型[J].現代防御技術,2002，30(3)：1-5. WANG Jun, LU Xiao-ping, LOU Shou-chun. The Situation Analysis Model in Air Defense Operation[J]. Modern Defense Technology, 2002, 30(3):1-5.

[11] 劉鴻福，潘梓逸，陶云.防空反導作戰部署的評估問題初探[C]∥防空反導作戰體系裝備與技術發展論文集,北京：兵器工業出版社,2014. LIU Hong-fu, PAN Zi-yi, TAO Yun. Preliminary Assessment of Air Defense Missile Combat Deployment[C]∥Beijing: Ordnance Industry Press, 2014.

[12] YOU D D,WANG F,YANG H,et al.The Problem Research about Firepower Compatibity of the Surface Warship Air Defense[J].Fir Control & Command Control,2004,29(6):1603-1605.

[13] NAVEH B Z，GUI A，LEVY E，et al. Theater Ballistic Missile Defense[C]∥ AIAA,2008,9:89-106.

[14] Boaz I Kaminer,Joseph Z Ben-Asher.A Methodology for Estimating and Optimizing Effectiveness of Non-Independent Layered Deifense[M].Wiley Inter Science 2009,8:119-129.

[15] 陳璟，任敏，劉鴻福,等.飛行器任務規劃[M] .長沙：國防科大出版社，2014. CHEN Jing, REN Min, LIU Hong-fu,et al. Aircraft Mission Planning.[M]. Changsha: National University of Defence Technology, 2014.

Combat Deployment Modeling and Analysis of Air Defense System in Combination with Missile-Gun

LIU Hong-fu, WENG Yu, WANG Zhi-qiang

(National University of Defense Technology,College of Mechatronics Engineering and Automation,Hunan Changsha 410073, China )

Deployment rules and methods of air defense system in combination with missile-gun are studied. On the basis of three basic deployment models (linear, fan-shaped and circular), analysis is made in detail on kill area and main parameters of air defense system with a combination of missile-gun, and on this basis characteristic value computation model of kill area is computed, mission planning system is used to do simulation, and correctness of model is validated.

mission planning； missile-gun combination air defense system； fire defense area； force deployment;fire distribution principle; defense system model

2015-10-13；

2016-03-02

國家自然科學基金(61403411)

劉鴻福(1983-)，男，湖南衡陽人。講師，博士，主要從事任務規劃、智能系統、自主協同控制、軌跡優化領域的研究。

10.3969/j.issn.1009-086x.2016.06.002

E844；N945.12

A

1009-086X(2016)-06-0007-06

通信地址：410073 湖南省長沙市國防科技大學三院自動化所三室

E-mail：330767967@qq.com