基于灰色聚類理論的非合作目標交會效能評估*

化金，朱學昌，王立旭

(北京宇航系統工程研究所，北京 100076)

空天防御體系與武器

基于灰色聚類理論的非合作目標交會效能評估*

化金，朱學昌，王立旭

(北京宇航系統工程研究所，北京 100076)

由于空間非合作目標航天器的特性不完全已知，將空間非合作目標視為灰色系統，利用灰色聚類理論評估交會效能。選擇跟蹤精度、預報精度、交會精度和交會窗口為評估指標，使用熵權法確定指標權重。考慮目標航天器變軌時刻和變軌加速度不同情況，分別仿真計算指標觀測值，評估交會效能。仿真算例評估結果說明效能評估方法具有客觀性和有效性。

航天系統工程；效能評估；灰色聚類；非合作目標；評估指標；信息熵

0 引言

空間非合作目標泛指不能提供有效合作信息的空間目標[1]，包括故障或失效衛星、空間碎片、廢舊航天器等。非合作目標交會技術是航天器在軌服務、空間垃圾清除[2]、空間對抗等熱門領域的關鍵技術[3]。與合作目標交會問題不同的是，非合作目標本身沒有配備目標識別器和交會敏感器[4]，而且姿態、軌道不受控制，出現自由翻滾、軌道下降的現象。

非合作目標的物理特性和運動特性是不完全已知的，屬于不確定性系統。概率統計、模糊數學、灰色系統理論和粗糙集理論是4種最常用的不確定性系統研究方法[5]。與概率統計研究“隨機不確定”對象、模糊數學解決“認知不確定”問題、粗糙集理論處理“邊界不清晰”情況不同，灰色系統理論以“部分信息已知，部分信息未知”的不確定性系統為研究對象，通過挖掘“部分”已知信息，提取有用信息，實現系統認知的目的。

空間非合作目標交會問題中包含了相對位姿測量、交會導航制導控制、抓捕與對接機構設計等關鍵技術，并需要多類傳感器和航天器組成系統實現交會任務。以往的研究中常以測量精度、導航精度、控制精度等單一指標評價交會問題的研究成果[6-8]，然而對交會系統在規定條件、規定時間內完成規定任務的程度[9]，即系統效能應該采用綜合指標進行評估。目前針對空間非合作目標交會效能評估方法的研究較少，本文利用灰色聚類理論，設計評估指標，建立空間非合作目標交會效能評估方法，并通過仿真算例說明評估方法的客觀性和有效性。

1 效能評估指標設計

空間非合作目標交會過程中，被動交會航天器稱為目標航天器，主動交會航天器稱為追蹤航天器。追蹤航天器在飛行的初始階段，距離目標航天器很遠，地基或者天基的測量控制系統搜索、跟蹤目標航天器軌跡，預報未來軌道，形成導航信息，向追蹤航天器發送制導指令，這個階段稱為遠距離導引段。當追蹤航天器上的交會敏感器捕獲目標航天器后，進入自主尋的段，控制系統導引追蹤航天器到達目標航天器附近某一點。最后根據具體的交會任務，追蹤航天器張開捕獲網或機械臂捕捉非合作目標，或者對目標進行伴飛、繞飛，或者以一定的相對姿態與目標對接。

測控系統的目標跟蹤、軌道預報和追蹤航天器的自主尋的、變軌交會都是空間非合作目標交會的重要環節。跟蹤精度、預報精度和交會精度影響交會任務的完成效果，所以應成為評估空間非合作目標交會的綜合效能指標。此外，由于非合作目標的特征不完全確定，交會窗口的長度會影響追蹤航天器應對目標航天器突發狀況的效果，因此也應成為評估指標之一。因此，交會效能評估指標包括：跟蹤精度、預報精度、交會精度和交會窗口。

2 評估指標計算模型

本文建立空間非合作目標交會仿真系統，通過仿真計算的方法獲取評估指標的數值。仿真系統包括目標航天器運動模型、目標跟蹤模型、軌道預報模型和追蹤航天器交會模型。

(1)目標航天器運動模型

在地心慣性坐標系下建立目標航天器的運動方程

(1)

式中：r=(x,y,z)為地心慣性坐標系下的位置矢量；v=(vx,vy,vz)為地心慣性坐標系下的速度矢量；a=(ax,ay,az)為地心慣性坐標系下的航天器推力加速度矢量；μ為地心引力常數；用下標tar代表目標航天器。

對于測控系統和追蹤航天器，已知目標航天器具有一定的變軌能力，但是未知目標變軌時刻、變軌加速度大小和形式。假設目標采取單脈沖變軌，變軌時刻為t1，變軌加速度為常值‖atar‖=aj，方向為軌道面的法線方向，變軌持續時間t。

(2) 目標跟蹤模型

假設測控系統、航天器上敏感器測量3個參數：目標與追蹤航天器的相對距離、視線俯仰角和視線方位角，利用擴展卡爾曼濾波算法(EKF)[10]估計目標的運動狀態X=(rtar,vtar,atar)，進行目標航天器軌跡跟蹤。跟蹤算法為

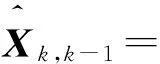
(2)

(3) 軌道預報模型

本文采用輸入為白噪聲的一階時間相關模型(Singer模型)[11]描述非合作目標的變軌加速度為

(3)

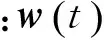
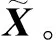
(4) 追蹤航天器交會模型

將目標航天器軌道坐標系選為追蹤航天器與目標航天器的相對運動參考坐標系，相對位置矢量為rrel=(x,y,z)，參考坐標系相對于地心慣性坐標系的角速度為目標航天器軌道角速度ω，則相對運動方程[8]為

(4)

式中：ax，ay，az為軌道坐標系下的加速度分量，下標cha代表追蹤航天器。

追蹤航天器在測控系統導引下飛向預設交會點，探測到目標變軌后，按照變軌策略在推力的作用下實施變軌，飛向新的交會點。交會過程如圖1所示，在交會時刻目標航天器與追蹤航天器的相對距離為交會誤差。當追蹤航天器采取不同的變軌策略，可在不同交會時刻以較小的誤差交會。將滿足交會誤差上限要求的交會時刻組成的時段定義為交會窗口Tj，追蹤航天器可在窗口內完成捕捉、對接或者伴飛等任務。每類任務對于交會誤差上限的要求不同，文本仿真計算時取5 m。在交會窗口內，交會誤差的平均值定義為交會精度δj=‖rrel‖。

圖1 空間非合作目標交會過程示意圖Fig.1 Sketch map of process of rendezvous with space noncooperative target

3 灰色聚類評估方法

灰色聚類評估主要用于“少數據”“貧信息”情況下的多指標系統評估[12]，設定若干個灰類，以反映評估對象不同的等級，如“優”、“良”、“中”、“差”。根據聚類對象不同，灰色聚類評估分為灰色關聯聚類評估和基于白化權函數的灰色聚類評估2類[13]。根據權重的不同，基于白化權函數的灰色聚類又分為灰色變權聚類和灰色定權聚類[14]。灰色關聯聚類評估主要用于歸并同類因素、簡化系統、減少不必要數據的收集。基于白化權函數的灰色聚類評估主要用于考察觀測對象屬于事先設定的某個類別。灰色變權聚類適用于指標意義、量綱皆相同的情形，而灰色定權聚類適用于指標意義或者量綱不同的情況。由于空間非合作目標交會問題物理意義明確，不需要簡化系統、合并同類項，評估指標意義、量綱不同，且在數量上差異較大，因此文本采用基于白化權函數的灰色定權聚類方法[14]。聚類評估方法具體步驟如下：

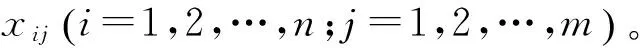
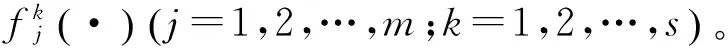
(5)

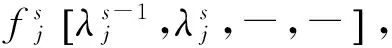
(6)

(7)

(8)

指標j的熵權為

(9)

第4步：根據指標權重和觀測值，計算灰色定權聚類系數

(10)

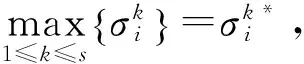
4 交會效能評估算例

4.1 算例仿真場景設定

設定非合作目標航天器分別按照表1中6種變軌參數飛行，以aj為標準，編號1，2可以看作目標“弱變軌”，而3～6為“強變軌”；以t為標準，編號1～4為“長時間”，而5,6為“短時間”；以t1為標準，編號1，3，5為“早變軌”，而2，4，6為“晚變軌”。通過上述3個參數的排列組合，可將目標變軌飛行分為6種與之對應的情況，并將這6種情況作為交會效能評估對象。以編號1的目標航天器變軌時刻為時間原點，從1 250～1 350 s每間隔5 s作為一個交會時刻，對追蹤航天器與目標交會的過程進行仿真。

表1 目標航天器變軌參數Table 1 Orbit transfer parameters of target spacecraft

圖2 中心點混合三角白化權函數示意圖Fig.2 Sketch map of mixed triangular whitenization weight function

4.2 效能評估

在21個交會時刻中，追蹤航天器對目標(編號1)的交會誤差如圖3所示。除1 250 s的交會誤差大于上限5 m以外，1 255～1 350 s的交會誤差均滿足要求，所以交會窗口為95 s。1 255～1 350 s的交會誤差平均值(交會精度)為1.89 m、跟蹤精度為21.90 m、預報精度為40 383 m。通過仿真計算，6個評估對象對4個交會評估指標：跟蹤精度、預報精度、交會精度和交會窗口(分別對應j=1,2,3,4)的指標值如表2所示。

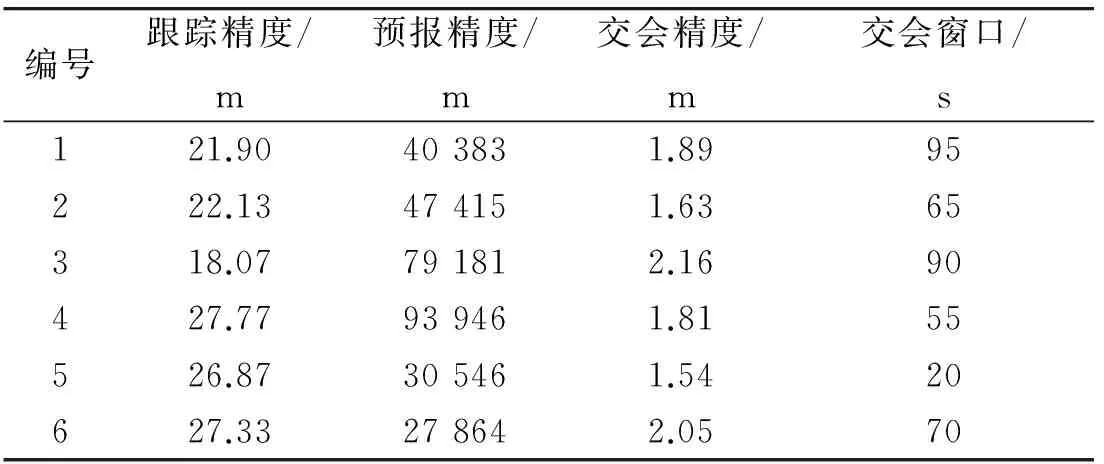
表2 效能評估指標值Table 2 Value of effectiveness evaluation index

從表2看出，在非合作目標交會的過程中，軌道預報精度遠遠低于目標跟蹤精度，相差3個量級。這是由于目標跟蹤時測控系統與交會敏感器的測量數據輸入到濾波算法中，將估計誤差維持在很小的范圍內波動，因此目標跟蹤的精度比較高。而軌道預報僅通過積分運動微分方程組得到估計值，初始值的誤差隨著時間逐漸累積到很大的數值。在仿真設置的變軌參數中，無論目標航天器進行早/晚、強/弱、長/短時間的變軌飛行，追蹤航天器都能在某時長的交會窗口內，以小于5 m的交會精度與目標航天器交會。

本文將4個指標分為 “優”、“良”、“中”、“差”(分別對應k=1,2,3,4)這4個灰類。對于前3個指標，誤差越小，精度越高，越有利于交會，權函數的轉折點從小到大排列。而對于交會窗口，時間越長，越有利于交會任務的完成，因此轉折點從大到小排列。結合經驗值，選取三角白化權函數的轉折點與中心點分別為

b3=5，

將觀測值進行歸一化處理，計算指標的熵權為

ω1=0.055 4，ω2=0.506 7，ω3=0.034 3，ω4=0.403 7.

從指標熵權來看，跟蹤精度和交會精度的變化很小，這2個指標的權重也小，總和接近0.1。交會窗口變化較大，預報精度變化最大，這2個指標的權重也大。說明了熵權法通過觀測值信息差異的大小決定指標的權重，并通過聚類系數反映到了評估結果中。相比利用專家打分等形式確定的指標權重，熵權法具有客觀性和可信性。4個指標觀測值的意義、量綱不同、數量上差距很大，相比灰色變權聚類方法，采用灰色定權聚類方法，可以充分發揮每個指標在聚類評估中的作用。

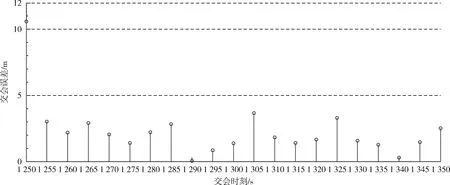
圖3 每個交會時刻的交會誤差Fig.3 Rendezvous error at each rendezvous time

計算灰色定權聚類系數，i=1時

0.403 7.

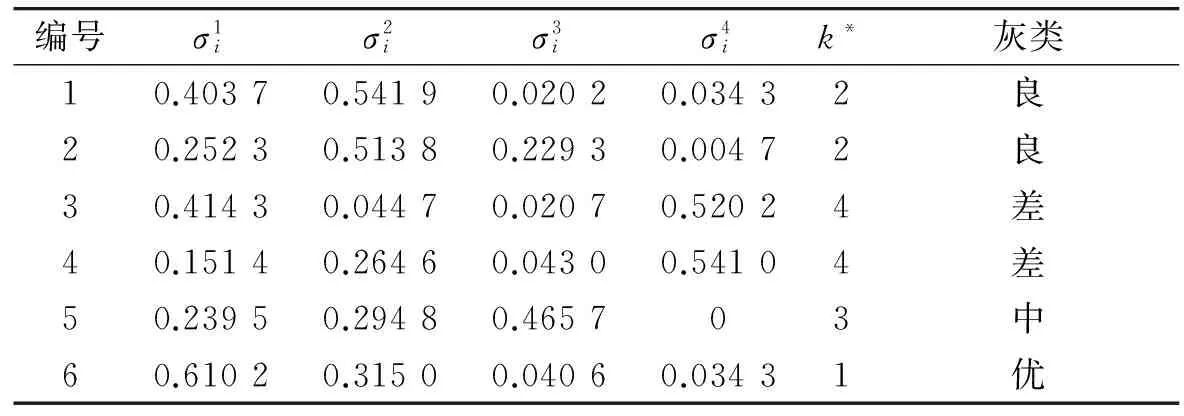
表3 聚類系數與評估結果Table 3 Clustering coefficient & evaluation result

4.3 評估結果分析

從表3看出，交會效能“優”的情況為編號6，“良”的情況為編號1和2，“中”的情況為編號5，“差”的情況為編號3和4。針對非合作目標航天器的不同變軌情況，無論變軌早晚，對于“長時間”、“強變軌”的目標航天器(編號3和4)，交會的評估結果是最差的。對于“長時間”、“弱變軌”的目標(編號1和2)，評估交會的結果是“良”，這是由于目標變軌前后軌道差異小于“強變軌”的情況，追蹤航天器與此類目標交會更加容易。對于“短時間”、“強變軌”的目標(編號5和6)，因為目標變軌時間短，測控系統預報誤差累積小，對交會誤差影響小。尤其是當目標“晚變軌”時，預報精度最高、交會窗口較長，導致交會效果較好，評價結果為“優”。但是當目標“早變軌”時，交會窗口變短，導致交會效果下降，評價結果為“中”。

綜合以上分析，效能評估的結果科學有效。相比選擇單一指標進行效能評估的方法，本文研究的方法更加客觀全面。

5 結束語

本文基于灰色聚類理論建立了空間非合作目標交會的效能評估方法。根據空間非合作目標交會的過程，選擇跟蹤精度、預報精度、交會精度和交會窗口為評估指標。在仿真系統中建立目標航天器運動模型、目標跟蹤模型、軌道預報模型和追蹤航天器交會模型。通過仿真算例說明了效能評估方法的客觀性和有效性。

[1] Committee on the Assessment of Options for Extending the Life of the Hubble Space Telescope, National Research Council. Assessment of Options for Extending the Life of the Hubble Space Telescope: Final Report[M]. Washington, WA, USA: National Academies Press, 2005.

[2] LEONOR M, BRUNO C. Covariance Analysis Tool for Far Non-Cooperative Rendezvous [C]∥AIAA Guidance, Navigation, and Control Conference, Boston, USA， August 19-22, 2013.

[3] 馬寶林，桂先洲. 空間非合作目標形式概念分析[J]. 吉首大學學報:自然科學版，2012，33(4)：87-90. MA Bao-lin, GUI Xian-zhou. Analysis of Formal Concept of the Space Non-Cooperative Target [J]. Journal of Jishou University:Natural Science ed, 2012,33(4): 87-90.

[4] 劉濤，解永春. 非合作目標交會相對導航方法研究[J]. 航天控制，2006，24(2)：48-53. LIU Tao, XIE Yong-chun. A Study on Relative Navigation for Spacecraft Rendezvous with a Non-Cooperative Target [J]. Aerospace Control, 2006, 24(2):48-53.

[5] 劉思峰，楊英杰，吳利豐. 灰色系統理論及其應用[M]. 北京：科學出版社，2014：113-115. LIU Si-feng, YANG Ying-jie, WU Li-feng. Grey System Theory and Application [M]. Beijing: Science Press, 2014: 113-115.

[6] XU Wen-fu, LIANG Bin, LI Cheng, et al. Autonomous Rendezvous and Robotic Capturing of Noncooperative Target in Space [J]. Robotica, 2010, 28(3): 705-718.

[7] 張立佳. 空間非合作目標飛行器在軌交會控制研究[D]. 哈爾濱：哈爾濱工業大學，2008. ZHANG Li-jia. Research on Control for Rendezvous with Noncooperative Target in Orbit [D]. Harbin: Harbin Institute of Technology, 2008.

[8] 陳密密. 用于空間非合作目標交會的相對測量算法研究[D]. 鄭州：解放軍信息工程大學，2009. CHEN Mi-mi. Research on Relative Measurement Algorithm of Space Rendezvous with A Noncooperative Target [D]. Zhengzhou: PLA Information Engineering University, 2009.

[9] 張杰. 效能評估方法研究[M].北京：國防工業出版社, 2009. ZHANG Jie. Study on Effectiveness Evaluation Theory [M]. Beijing: National Defense Industry Press, 2009.

[10] 秦永元. 卡爾曼濾波與組合導航原理[M]. 西安：西北工業大學出版社，2012：51-52. QIN Yong-yuan. Kalman Filter and Integrated Navigation Theory [M]. Xi’an: Northwestern Polytechnical University Press, 2012:51-52.

[11] 潘泉. 現代目標跟蹤與信息融合[M]. 北京：國防工業出版社，2009. PAN Quan. Modern Target Tracking and Information Fusion [M]. Beijing: National Defense Industry Press, 2009.

[12] 余靜，張勇濤，張松良. 基于灰色聚類理論的C4ISR系統效能評估研究[J]. 現代防御技術，2009，37(3)：64-67. YU Jing, ZHANG Yong-tao, ZHANG Song-liang. Evaluation Method of C4ISR System Effectiveness Based on Grey Cluster Theory [J]. Modern Defense Technology, 2009, 37(3):64-67.

[13] ZHANG Ke, LIU Si-feng. Research on Extended Cluster of Grey Incidence and Its Application [C]∥2009 IEEE International Conference on Grey Systems and Intelligent Services, Nanjing, China，November 10-12, 2009.

[14] 王正新，黨耀國，劉思峰. 基于白化權函數分類區分度的變權灰色聚類[J]. 統計與信息論壇，2011，26(6): 23-27. WANG Zheng-xin, DANG Yao-guo, LIU Si-feng. Grey Clusters with Variable Weights Based on the Classification Degree of the Whitening Weight Functions [J]. Statistics & Information Forum, 2011, 16(6):23-27.

[15] 米傳民，劉思峰，黨耀國，等. 灰色熵權聚類決策方法研究[J]. 系統工程與電子技術，2006，28(12)：1823-1825. MI Chuan-min, LIU Si-feng, DANG Yao-guo, et al. Study on Grey Entropy Weight Clustering Decision-Making [J]. Systems Engineering and Electronics,2006,28(12):1823-1825.

Effectiveness Evaluation of Rendezvous with Space Non-Cooperative Target Based on Grey Clustering Theory

HUA Jin，ZHU Xue-chang, WANG Li-xu

(Beijing Institute of Aerospace Systems Engineering, Beijing 100076,China)

Due to the uncertainty of space non-cooperative target, the target is regarded as a grey system, and the effectiveness evaluation of rendezvous is based on grey clustering theory. Tracking precision, predicting precision, rendezvous precision and rendezvous window are chosen as indicators, and their weights are decided by entropy. Considering different orbit transfer time and acceleration, the data of indicators are calculated respectively by simulation, and the effectiveness of rendezvous is evaluated with thegrey cluster method. Simulation result shows that effectiveness evaluation method is of objectivity and credibility.

aerospace systems engineering; effectiveness evaluation; grey clustering; non-cooperative target; evaluation index; entropy

2015-11-19；

2016-02-16

化金(1991-)，女，北京人。碩士生，主要研究方向為飛行器設計研究。

10.3969/j.issn.1009-086x.2016.06.003

V57;TP301.6

A

1009-086X(2016)-06-0013-06

通信地址：100076 北京9200信箱10分箱10號

E-mail：huajin112358@163.com