基于軌跡預測的二階DPA擴散抑制方法*

孫承鋼，張奕群，2

(1.北京電子工程總體研究所，北京 100854； 2. 北京仿真中心 航天系統仿真重點實驗室，北京 100854)

探測跟蹤技術

基于軌跡預測的二階DPA擴散抑制方法*

孫承鋼1，張奕群1，2

(1.北京電子工程總體研究所，北京 100854； 2. 北京仿真中心 航天系統仿真重點實驗室，北京 100854)

二階動態規劃算法(DPA)是一種有效的點目標檢測算法，能夠在低信噪比條件下檢測目標，但也存在著評價函數擴散等缺點。針對二階DPA的這一不足，提出了抑制二階DPA評價函數擴散的方法。與其他抑制方法相比，提出的方法既有效地降低了噪聲對檢測過程的影響、抑制了評價函數擴散的現象、提高了對目標的檢測能力，又更適合于硬件實現。

目標檢測；Markov過程；動態規劃；軌跡預測；卡爾曼濾波；評價函數擴散

0 引言

點目標檢測與跟蹤，特別是低信噪比條件下的點目標檢測與跟蹤，一直是一個困難的問題，這是由于點目標沒有形狀和紋理特征，而且信噪比比較低時，目標的灰度與噪聲相仿，所以很難將目標與噪聲區分開來，以致對點目標的檢測和跟蹤十分困難。

從20世紀六七十年代起，人們開始系統地研究點目標跟蹤問題，并提出全局最近鄰(GNN)算法[1]、概率數據關聯(PDA)算法[2]、聯合概率數據關聯(JPDA)算法[3-4]、多假設跟蹤(MHT)算法[5-7]、動態規劃算法(DPA)[8-9]等多種算法，其中DPA是一種重要的先跟蹤后檢測算法，也是目前最有效的低信噪比跟蹤算法，它通過逆向分步尋優實現在跟蹤過程中檢測目標，取得了檢測效果和計算量上的平衡。然而DPA也存在著一些不足[10]，例如檢測過程容易受到噪聲干擾、由于評價函數擴散導致的目標覆蓋等。

由于DPA存在上述不足，有人提出了基于二階Markov過程的DPA[10](簡稱二階DPA)，該算法改善了對低信噪比運動目標的檢測能力，縮短了所需的檢測幀數，但是對評價函數擴散的抑制并不理想，所以文獻[10]中專門提出了一種抑制評價函數的方法，但該方法不適合于硬件實現。為了解決上述問題，本文提出了一種方法，該方法既能有效抑制評價函數的擴散，又比較適合于硬件實現。

1 基于二階Markov過程的DPA[10]

二階DPA是文獻[10]首次提出的，其基本內容介紹如下。在基于二階Markov過程的DPA中采用的評價函數[11]為

s(θ(k),θ(k-1),…，θ(1)) =

(1)

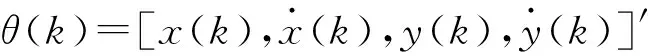
由于式(1)的計算量很大，為簡化尋優過程，將式(1)中的分式部分整理為遞推形式：

P(θ(k)|θ(k-1),θ(k-2),…,θ(1))·

(2)

假設目標滿足二階Markov模型，則式(2)等號右側的狀態轉移概率P(θ(k)|θ(k-1),θ(k-2),…,θ(1))可簡化為

P(θ(k)|θ(k-1),θ(k-2),…,θ(1))=

P(θ(k)|θ(k-1),θ(k-2)),

k≥3.(3)

定義：

Θk

并令

lnP(θ(k)|θ(k-1),θ(k-2))，k=3,

lnP(θ(2)|θ(1))，

結合式(1)及(2)，(3)，得到遞推形式的評價函數：

s(θ(k),θ(k-1)…,θ(1))=a(k)+s(θ(k-1),

…,θ(1))，k≥3,

s(θ(2))=a(2)+s(θ(1)).

(4)

在DPA中，評價函數最大的軌跡認為是目標的真實軌跡，因此

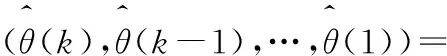
(5)

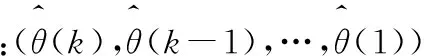
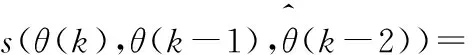
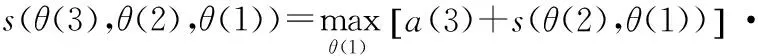
s(θ(2),θ(1))=a(2)+s(θ(1)).

(6)

根據位置的估計誤差，就可以確定搜索范圍。由于搜索范圍減小，二階DPA中評價函數擴散范圍與傳統DPA相比要小。為了進一步抑制評價函數擴散，文獻[10]提出了一種抑制評價函數擴散的方法。該方法將整幅圖像分成了2部分，一部分是包含目標的關聯區域；另一部分則是未檢測出目標的區域。通過將目標軌跡的關聯始終限制在關聯區域內，減小關聯到目標軌跡上的噪聲數量，從而達到抑制評價函數擴散的目的。該方法在軟件仿真時有著良好的抑制效果，但在實際應用中會遇到以下問題：第一，在對圖像進行處理時，該方法首先對搜索區域內的軌跡進行關聯。由于搜索區域可能在圖像的任意位置，所以在實際處理前必須獲取到整幅圖像的數據信息，這會浪費大量的時鐘周期。第二，目標搜索區域的個數和大小不固定，導致在硬件設計時必須預先留出足夠的資源，而這極易導致硬件資源的浪費。

由于上述缺點的存在，導致該算法的實時性較差、硬件資源的消耗也比較大。鑒于以上原因，提出了一種基于軌跡預測的擴散抑制方法，該方法既能夠很好的抑制評價函數擴散，又更適合于硬件實現。

2 基于軌跡預測的擴散抑制方法

文獻[10]的擴散抑制方法的關鍵就是劃定目標關聯區域，將能夠與目標軌跡關聯的像元限制在該區域內，從而實現對擴散的抑制。但這樣做就會產生上一節中所述的2個缺點。所以提出利用軌跡預測來抑制評價函數擴散的方法，因為在此方法中不再需要劃定目標關聯區域，從而避免了劃定目標關聯區域所帶來的問題。

2.1 原理分析

對于一幅分辨率為M×M的圖像，其像素點的測量值z(k)通常有如下定義：

式中：1≤i,j≤M，zij(k)為像素點(i,j)的觀測值并滿足如下關系[12]：

式中：μ>0。從上式可以看出，目標所在觀測數據的均值一定比噪聲的均值大。因此，所有通過DPA檢測到的軌跡中，目標軌跡的評價函數是最大的。

根據DPA中的尋優關系，所有像素點都是關聯到其附近的評價函數最大的軌跡上，這就使得會有多個像素點關聯到目標軌跡上，如圖1所示，導致目標周圍像素點的評價函數增大，出現評價函數擴散現象。因此如果能夠減少與目標軌跡關聯的像素數量，就能夠有效降低評價函數的擴散程度。

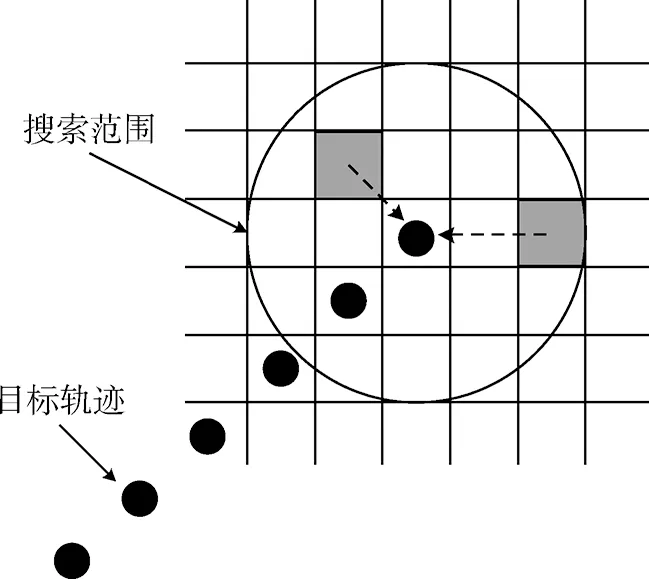
圖1 評價函數擴散的原因Fig.1 Reason of merit function scattering

2.2 基于軌跡預測的擴散抑制方法

根據上述分析，在式(6)中引入權重ω：

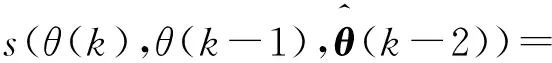
s(θ(2),θ(1))=a(2)+s(θ(1))，

(7)

擴散抑制方法的具體實現，如圖2所示。可分為以下幾個步驟：

(1) 根據二階DPA確定搜索范圍Rs；

(2) 根據式(6)計算評價函數；

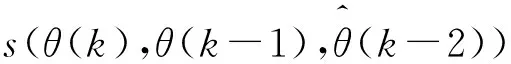
從實現步驟中可以看出，擴散抑制方法不需要劃定關聯區域，可以對獲取到的像元信息進行實時處理，從而節約大量的時鐘周期。同時擴散抑制方法的算法結構固定，其實現過程中其所需的硬件資源固定，不會出現硬件資源的浪費。由此可以看出，此方法很好的克服了文獻[10]中方法所存在的2個缺點。

2.3 狀態估計

在估計目標狀態前，先要建立目標運動模型。設在第k幀時，目標的運動狀態為

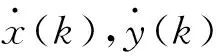
假設目標不機動，即目標的運動軌跡基本上是一條直線，其運動狀態模型[13-14]為

θ(k+1)=Fkθ(k)+Gkv(k)，

式中：

式中：Tk+1是第k+1幀圖像與第k幀圖像間的時間間隔；v(k)為0均值的白噪聲；狀態誤差滿足：

第k幀圖像的觀測模型為

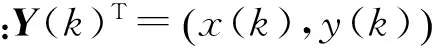
Rk

為了方便，假設圖像中的噪聲為0均值的白噪聲。

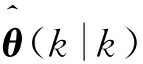
圖2 擴散抑制方法的實現過程Fig.2 Realization of method for restraining merit function scattering

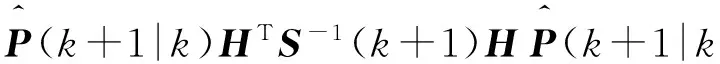
3 仿真驗證

下面通過仿真來說明擴散抑制方法對評價函數擴散的抑制效果。實驗的詳細參數如表1所示。

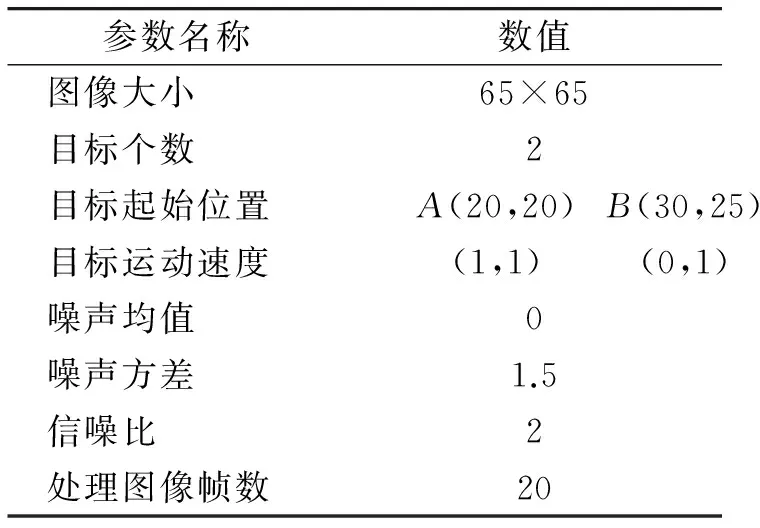
表1 實驗參數Table 1 Parameter of test

其中，信噪比定義為目標灰度和噪聲方差之比。

通過比較圖3和圖4可以看出，文中提出的擴散抑制方法能夠有效地抑制評價函數擴散，其抑制效果與文獻[10]中方法的抑制效果相差不多。在圖4中，目標位于評價函數最大的2個像素點處，評價函數的擴散已經被抑制掉，只要給定合適的閾值，就可以直接將目標確定出來。

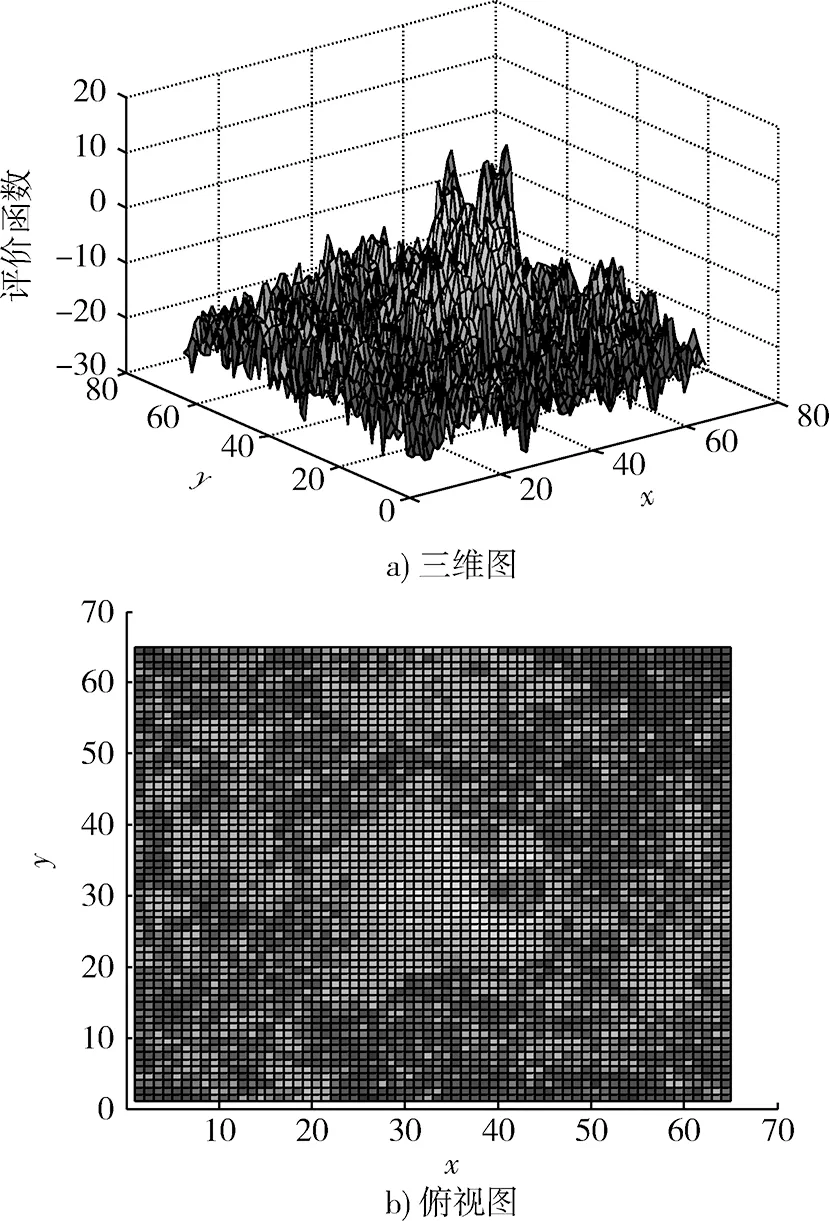
圖3 二階DPA的評價函數Fig.3 Merit function of second-order DPA

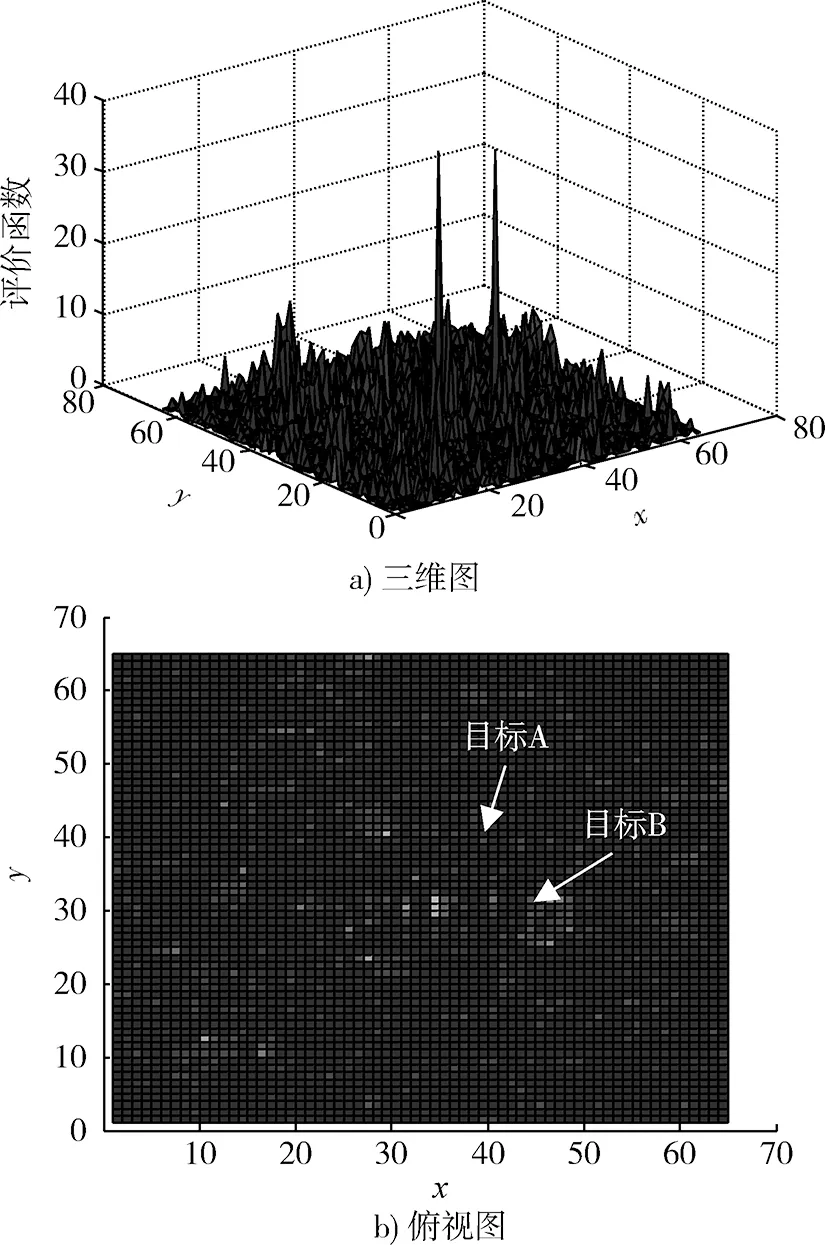
圖4 擴散抑制方法的評價函數Fig.4 Merit function of method for restraining merit function scattering

4 結束語

本文提出了一種抑制二階DPA評價函數擴散的方法。通過引入目標運動狀態，減小搜索范圍大小，進而抑制評價函數的擴散。仿真結果表明，該方法能夠有效的抑制評價函數擴散。從表面上看由于引入卡爾曼軌跡預測使得算法的計算變得極為復雜，實際上由于目標運動模型中的矩陣都是稀疏矩陣，使得卡爾曼遞推計算過程變得非常簡單，很容易硬件實現。但是因為目標在搜索范圍R′內的概率小于1，導致算法的檢測概率有一定程度的減小，如何克服這一缺點還有待于進一步研究。

[1] BLACKMAN S, POPOLI R. Design and Analysis of Modern Tracking Systems[M].Country Norwood,United States: Artech House, 1999.

[2] BAR-SHALOM Y, KIRUBARAJAN T, LIN X. Probabilistic Data Association Techniques for Target Tracking with Application to Sonar, Radar and EO Sensors[J]. IEEE Aerospace and Electronic Systems Magazine, 2005, 20(8): 37-56.

[3] FORTMANN T E, THOMAS E, BAR-SHALOM Y, et al. Sonar Tracking of Multiple Targets Using Joint Probabilistic Data Association[J]. IEEE Journal of Oceanic Engineering, 1983, 8(3): 173-184.

[4] BAR-SHALOM Y, FORTMANN E T. Tracking and Data Association[M].New York:Academic Press, 1988

[5] REID D B. An Algorithm for Tracking Multiple Targets[J]. IEEE Trans. on Automatic Control,1979, 24(6):843-854.

[6] REID D B.A Multiple Hypothesis Filter for Tracking Multiple Targets in a Cluttered Environment[R]. Lockheed Missiles and Space Company Report, 1977.

[7] BLACKMAN S S. Multiple Hypothesis Tracking for Multiple Target Tracking[J]. IEEE Aerospace and Electronic Systems Magazine, 2004, 19(1): 5-18.

[8] BARNIV Y. Dynamic Programming Solution for Detecting Dim Moving Targets[J]. IEEE Trans. on Aerospace and Electronic Systems,1985, 21(1): 144-156.

[9] BARNIV Y,KELLA O. Dynamic Programming Solution for Detecting Dim Moving Targets Part II: Analysis[J]. IEEE Trans. on Aerospace and Electronic Systems, 1987,23(6):776-788.

[10] 王碩. 基于二階Markov過程的動態規劃法及其在點目標檢測中的應用[D].北京：中國航天科工第二研究院，2015. WANG Shuo. Dynamic Programming Algorithm Based on Second-Order Markov Process and Its Application on Point Target[D].Beijing: The Second Research Academy of CASIC,2015.

[11] ARNOLD J, SHAW S, PASTERNACK H. Efficient Target Tracking Using Dynamic Programming[J]. IEEE Trans. on Aerospace and Electronic Systems,1993, 29(1): 44-56.

[12] TONISSEN S M, EVANS R J. Performance of Dynamic Programming Techniques for Track-Before-Detect[J]. IEEE Trans. on Aerospace and Electronic Systems,1996, 32(4): 1440-1451.

[13] PULFORD G W, LA SCALA B F, Over-the-Horizon Radar Tracking Using the Viterbi Algorithm-Second Report to High Frequency Radar Division[R]. University of Melbourne, Technical Report CSSIP 16/95, Aug. 1995.http://web.ukonline.co.uk/gpulford/Pdf doc/vda-rep2.pdf.

[14] PULFORD G W, LA SCALA B F. Over-the-Horizon Radar Tracking Using the Viterbi Algorithm-Third Report to High Frequency Radar Division[R]. University of Melbourne, Technical Report CSSIP 27/95, Dec. 1995. http://web.ukonline.co.uk/gpulford/Pdf doc/vda-rep3.pdf.

[15] PULFORD G W, LA SCALA B F. Multihypothesis Viterbi Data Association: Algorithm Development and Assessment[J]. IEEE Trans. on Aerospace and Electronic Systems, 2010, 46(2): 583-609.

Restraint Method for Merit Function Scattering of Second-Order DP Algorithm Based on Trace Prediction

SUN Cheng-gang1, ZHANG Yi-qun1，2

(1.Beijing Institute of Electronic System Engineering,Beijing 100854, China；2.Science and Technology on Special System Simulation Laboratory,Beijing 100854,China)

The second-order dynamic programming algorithm (DPA) is effective on target detection. The low SNR target can be detected with this algorithm. But the algorithm still has some shortages like merit function scattering. Aiming at the shortage of the second-order DPA, a method is put forward to restrain the merit function scattering. With the method, the impact of noise on the detection process can be reduced, and the merit function scattering can be restrained. The method hasbetter detection ability,and can be implemented on hardware much more easily.

target detection; Markov process; dynamic programming; trace prediction; Kalman filter; assessment function scattering

2016-03-08；

2016-05-15

有

孫承鋼(1990-)，男，遼寧大連人。碩士生，主要研究方向為導航、制導與控制。

10.3969/j.issn.1009-086x.2016.06.015

TN953；N945.13

A

1009-086X(2016)-06-0085-06

通信地址：100854 北京142信箱30分箱

E-mail：15311449734@189.cn