滲透的是思想 孕育的是策略

陳志鳳

[摘要]小學數學教材編排是以數學知識的發生、發展、運用為主線，知識內容是顯而易見的，但對于數學知識中所蘊含的數形結合思想教材并未明確指出，尤其是在解決問題的策略單元教學中，合理地運用數形結合的思想，有助于化抽象為直觀，打破學生的思維局限；有助于學生解決具體的問題；有助于拓展學生尋找解決問題的途徑，從而促進學生策略的形成，提高分析問題和解決問題的能力.

[關鍵詞]數形結合思想；有效滲透；策略形成

隨著社會的發展，要想實現終身學習和人的可持續發展，在教育中發展學生的能力，使之掌握獲得知識和進一步學習的方法，逐漸掌握蘊涵在知識內的思想和方法也就顯得尤為重要，小學數學涉及的數學思想有很多，如數形結合思想、函數思想、轉化思想、分類討論思想……用數學思想引領數學課堂，對學生解決問題的策略形成必將有質的提升.小學是學生學習數學知識的啟蒙時期，在數學教學中運用數形結合思想，不但符合學生的認知規律，而且能引起學生的學習興趣，激發學生的學習積極性，提高學生分析問題和解決問題的能力.

小學數學教學中滲透數形結合思想的意義

1.滲透數形結合的思想，培養思維的靈活性和創造性

數形結合具體地說就是將抽象的數學語言與直觀圖形結合起來，通過“數”與“形”之間的對應和轉換來解決數學問題.著名數學家華羅庚指出：“數缺少形時少直觀，形少數時難入微.”這句話說明了“數”和“形”是緊密聯系的，由數想形，以形助數的數形結合思想在解答問題時，具有可以使問題直觀呈現的優點，有利于加深學生對知識的識記和理解；有利于學生分析題中數量之間的關系，豐富表象，引發聯想，啟迪思維，拓寬思路，迅速找到解決問題的方法，從而提高分析問題和解決問題的能力.它可以借助簡單的圖形、符號和文字所作的示意圖，促進學生形象思維和抽象思維的協調發展，溝通數學知識之間的聯系，從復雜的數量關系中凸顯最本質的特征，例如，我們常用作線段圖、樹形圖、長方形面積圖、集合圖、數軸等，幫助學生理解抽象的數量關系、數學概念，使問題簡明直觀，這些都體現了數形結合的思想，在解決問題的過程中，提高學生的思維能力和數學素養，適時地滲透數形結合的思想，可達到事半功倍的效果.

2.應用數形結合思想，增強思維的廣闊性和深刻性

“數形結合”是一種重要的數學思想，對教師來說是一種教學策略，是一種發展性課堂教學手段；對學生來說則又是一種學習方法.數形結合思想形成的前提是讓學生經歷應用的歷練，而教師提供時間與空間是“方法”提升為“思想”的保證，如果長期滲透，運用恰當，則使學生形成良好的數學意識和思想，長期穩定地作用于學生的數學學習生涯中.在教學中，教師應充分利用學生形象思維的特點大量地用“形”解釋、演示，幫助理解抽象的“數”.

數形結合思想在解決問題的策略教學中的滲透與應用

蘇教版數學教材從第二學段開始，每冊編排了一個“解決問題的策略”單元，依次介紹了列表、畫圖、一一列舉、轉化、假設等解決問題的基本策略.“形成解決問題的一些基本策略，體驗解決問題策略的多樣性，發展實踐能力和創新精神”是《數學課程標準（2011版）》確定的課程目標之一，教材編寫“解決問題的策略”這樣的單元，就是為了貫徹落實這樣的課程目標.解決問題的策略是在長期數學教學中不斷培養的，是通過各個領域內容的教學逐漸形成的，單獨編寫“解決問題的策略”這樣的單元，能加強策略的形成和對策略的體驗.怎樣在教學中滲透基本的數學思想，幫助學生提高解決問題的能力，形成解決問題的一些基本策略，一直是值得每位教師認真思考的問題.本文結合筆者執教的三次“解決問題的策略”的課例，就數形結合的思想方法在“解決問題的策略”單元教學中的有效應用談談自己的認識.

1.數形結合：化抽象為直觀，打破學生思維局限

在中高年級的數學教學中，學生在解決有一定思維難度的數學問題時，常常會被題目中繁雜的信息所困擾，不知從何下手，尤其是行程問題和圖形的面積變化問題，而畫圖可以將題目中的信息簡潔地表示在圖中，學生根據所揭示的數學問題內涵，采用畫線段圖或面積變化圖的方法，把抽象的問題具體化、直觀化，從而找到解決問題的突破口，形成解決問題的策略.可見，“畫圖策略”是解決問題的常用方法，是“數形結合”思想的具體體現，

案例1：蘇教版四年級下冊《用“畫圖”的策略解決問題》片段回放：

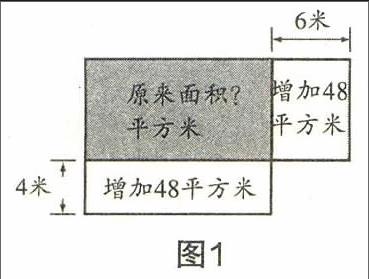
出示題目1：東關小學有一塊長方形試驗田.如果這塊試驗田的長增加6米，或者寬增加4米，面積都比原來增加48平方米，你知道原來試驗田的面積是多少平方米嗎？

師：怎樣理解這道題？（大家互相說一說，討論一下）

師啟發：長增加的時候，寬增加嗎？寬增加的時候，長增加嗎？

指示學生回答，師總結并出示課件：

如果長增加6米，寬不變，面積比原來增加48平方米；

如果寬增加4米，長不變，面積比原來增加48平方米，

生畫圖，師指導，突出說明兩個增加的部分不能相連， 解答：48÷6=8（米），48÷4=12（米），12x8=96（平方米）.

師總結：通過畫圖我們把復雜的問題變簡單，抽象的文字變直觀.這就是畫圖策略的重要作用.并板書：復雜——簡單；抽象——直觀.

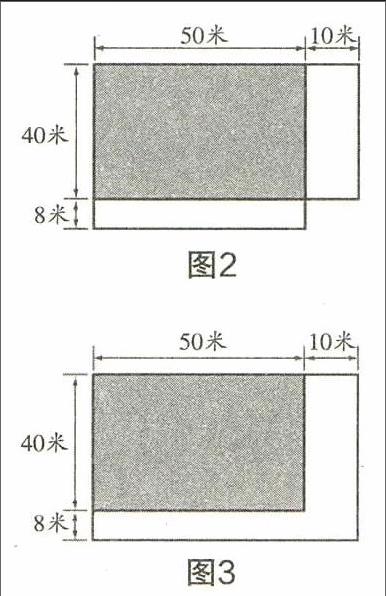
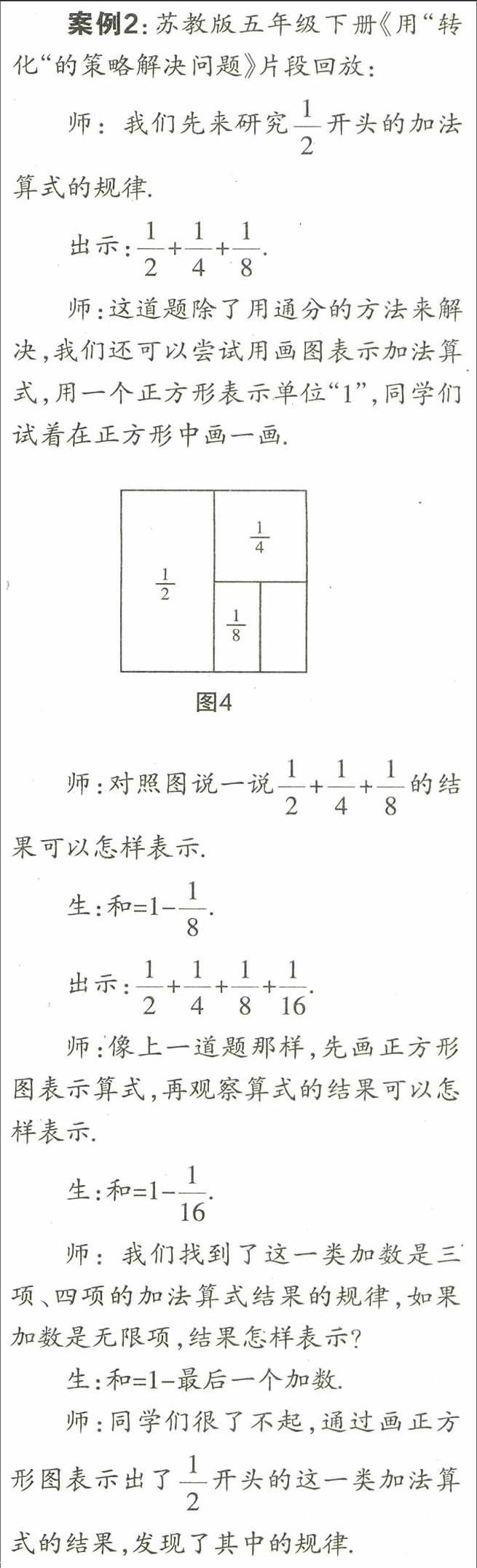
出示題目2：王營小學原來有一個長方形操場，長50米，寬40米，擴建校園時，操場的長增加了10米，寬增加了8米，操場的面積增加了多少平方米？

學生畫圖，呈現兩種不同情況.

引導學生結合題意進行討論，師：你們認為哪一種畫法符合題目的意思？為什么？（師組織學生討論，最后得出正確的答案）

學生在解答這個問題時情況也很多，出現了四種不同的解答方法.

通過數形結合（畫圖），讓學生在圖中表征題目中的信息，使原本復雜的題意直觀化、形象化，打破學生思維的局限性，讓解決問題的方法多樣化，這樣的教學從簡單到復雜，層層推進，充分體現了開放性、綜合性和應用性.通過兩個問題的嘗試、比較、探索，學生掌握了解決此類問題的基本方法，形成了畫圖的基本策略，激發了學習的興趣，激起了探究的欲望，endprint

‘

2.數形結合：學生解決具體問題的“向導”

在小學數學教學中，恰當地運用數形結合的思想方法，能將抽象的數學語言與直觀的圖象結合起來，把復雜的問題簡單化，抽象的問題形象化，從而較好地突破教學難點，促進學生的數學學習，

案例2：蘇教版五年級下冊《用“轉化“的策略解決問題》片段回放：

師：我們先來研究 開頭的加法算式的規律.

出示：

師：這道題除了用通分的方法來解決，我們還可以嘗試用畫圖表示加法算式，用一個正方形表示單位“1”，同學們試著在正方形中畫一畫.

本節課的教學目標之一是讓學生經歷有序的探究過程，體驗數學規律的形成過程，感悟探究數學規律的一般方法.教師在呈現問題時也很有序，先研究加數是三項，再研究四項，在此基礎上拓展到無限項，符合學生的認知邏輯.這個過程能讓學生初步體會到用直觀的“形”表示抽象的“式”二者的和諧統一，從而使問題得以巧妙地解決.

3.數形結合：拓展學生尋找解決問題的途徑

運用數形結合有時能使數量之間的內在聯系變得比較直觀，成為解決問題的有效方法之一.在分析問題的過程中，注意把數和形結合起來考察，根據問題的具體情形，把圖形的問題轉化為數量關系的問題，或者把數量關系的問題轉化為圖形的問題，使復雜問題簡單化，抽象問題具體化，化難為易，

案例3：蘇教版六年級下冊《解決問題的策略》片段回放：

出示題目：全班42人去公園劃船，租10只船正好坐滿.每只大船坐5人，每只小船坐3人.租的大船、小船各有多少只？

應該給學生足夠的時間思考：解決這個問題，你準備選擇什么策略？

生1：畫圖：先畫10只大船坐50人，再去掉多的8人

生2：一一列舉：從大船有9只、小船有1只開始，有序列舉，

生3：假設：假設大船和小船同樣多，再根據總人數調整，

在上面這個片段中，數形結合很好地促進學生聯系實際，靈活解決數學問題，而且還有效地防止了學生的生搬硬套，打開了學生的解題思路，由不會解答到用多種方法解答，逐步讓學生感悟到了不同策略中的共有規律，引發了學生的創新思路，它將學生頭腦中原有的思維方式進行了更新，拓展了學生尋找解決問題的途徑，從而提高了解決數學問題的能力.endprint