圖片——圖形——圖理

高峰官

[摘要]空間與圖形的入門課便是讓學生走進《豐富的圖形世界》，筆者立足學生已有的生活經驗和知識背景，理清了教學思路，精心設計了三個教學模塊：從生活到圖片，讓數學貼近學生生活；從圖片到圖形，讓學生用數學眼光看待世界，增強數學抽象概括能力；從圖形到圖理，讓學生探尋規律、領悟數學知識的奧秘.在實際教學中，師生互動、生生互動，達到了很好的教學生成，實現了教學目標的三者融合.

[關鍵詞]圖片；圖形；圖理；數學規律

初中數學課程有四大模塊：數與式、空間與圖形、概念與統計、實踐與探究.其中空間與圖形的入門課便是讓學生走進《豐富的圖形世界》.能否激起學生的好奇心、激發學生的學習興趣，能否引發學生的探究熱情，能否增強學生學好幾何的信心，這節啟始課的教學顯得特別重要，為此，筆者立足學生已有的生活經驗和知識背景，理清了教學思路，精心設計了三個教學模塊：從生活到圖片，讓數學貼近學生生活；從圖片到圖形，讓學生用數學眼光看待世界，增強抽象概括能力；從圖形到圖理，讓學生探尋規律、領悟數學的奧秘，在實際教學中，師生互動、生生互動，達到了很好的教學生成，實現了教學目標的三者融合.

本節課的設計思路清晰獨特，數學來源于生活，從生活中抽象出幾何體，通過觀察、討論、比較，我們認識了幾何體的構成，初步了解到幾何體的特征，這將為學生今后學好數學揭開新的一頁，讓學生走近幾何圖形的世界.

從生活到圖片，讓數學貼近學生生活

數學學習從來都不是紙上談兵、空中樓閣，而應建立在豐富的生活背景與學生已有知識經驗基礎上.數學新課程觀念強調，數學學習要多聯系生活實際，要讓學生多感受生活，多從生活具體問題中提煉出數學問題，從而促進學生形成正確的數學學習觀.

在這一教學環節，筆者從網上搜索或用照相機拍攝了許多包含常見幾何圖形的精美圖片，如埃及金字塔、北京天壇、城市高樓建筑、上海的東方明珠、火箭、時鐘、文具盒、書本、鉛筆、魔方、三棱鏡、圣誕老人的帽子、足球、奧運五環旗、一些包含幾何圖形的藝術品等，這些圖片的展示，一下子激發起了學生學習的興趣，讓學生感受到數學就在身邊，生活離不開數學.屏幕展示出來的圖片，看似漫不經心，實際上是教師精心預設的——從這些圖片中都可以抽象出一些基本的數學圖形.

從圖片到圖形，讓學生用數學眼光看世界

數學教學要引導學生將生活中的問題轉化為數學問題，從而形成正確的數學觀.從小學到初中，學生的思維方式將發生較大的變化，由具體形象思維到抽象邏輯思維，進入初中數學學習，無論是代數學習，還是幾何學習，教師都要關注學生抽象概括能力的發展，

在這一教學環節，筆者設計_r這樣幾個活動：

活動一：觀察生活中的圖片，感受數學中的圖形.

從生活中的圖形抽象出長方體、正方體、球、圓柱、圓錐、棱柱、棱錐等，這些都是立體圖形.

活動二：認識數學中幾何體的分類，

幾何體可分為柱體、錐體與球體.柱體有圓柱與棱柱；錐體有圓錐和棱錐.

如果按幾何體是否全由平面構成，那么可分為多面體與非多面體.多面體有棱柱、棱錐，非多面體有圓柱、圓錐和球體.

分類需按一定的標準進行，分類討論是認識數學世界、分析問題、解決問題的一種重要的數學思想方法.

活動三：理解數學圖形的組成.

點動成線，線動成面，面動成體，幾何圖形是由點、線、面構成的，面與面相交得到線，線與線相交得到點.

接著以棱柱、棱錐為例，重點介紹組成部分的名稱，如底面、側面、頂點、高等概念，并對棱、側棱、頂點作出明確的說明，

引導學生進一步觀察比較：棱柱、棱錐有哪些不同點、相同點？ 通過這一環節的教學，讓學生從具體豐富的物體中，抽象出幾何圖形，這是一個從具體到抽象的思維過程；引導學生對幾何體進行分類，讓學生領會分類的思想方法，讓學生有條理地分析思考問題；理解數學圖形的組成，進一步深入圖形世界，為后續深入研究每一種圖形的性質、運算和推理打好基礎，在分析幾何體組成的同時，教師向學生滲透了將空間幾何體轉化為平面圖形的思維策略，這就是數學學習的一種重要思想方法——化歸思想.

從圖形到圖理，讓學生領悟數學知識的奧秘

在這一教學模塊中，筆者創設了三個問題情境，采用了觀察、操作、探究、討論、協作交流的方式讓學生探討圖理——圖形中蘊含的數學規律，讓學生感受圖形世界的奧妙無窮，從而很好地激發學生學習、探究的興趣.

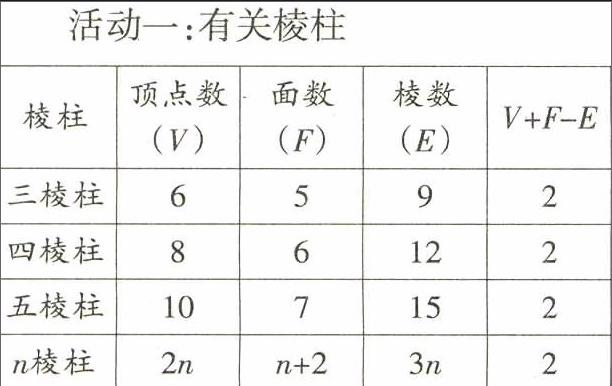
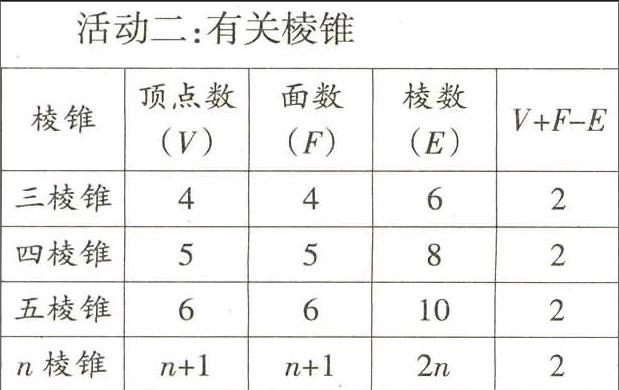
問題情境一：讓學生探究有關多面體面數、頂點數和棱數之間的內在聯系.

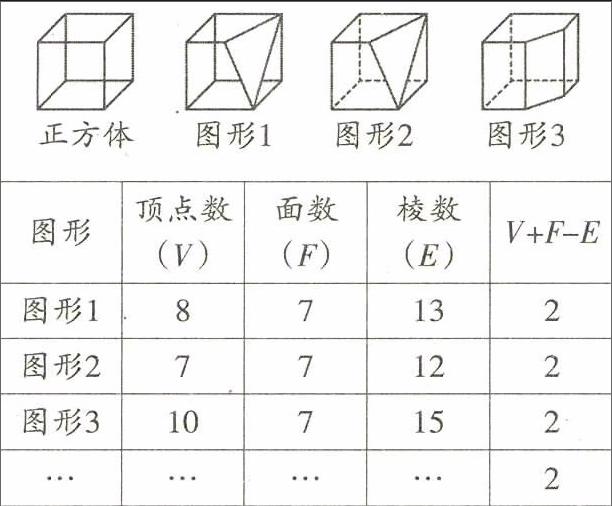
活動三：將下圖中的正方體切去一小塊，它們各有多少個面？多少條棱？多少個頂點？

由上面的探究過程可得出—個結論：頂點數（V）+面數（F）-棱數（E）=2.

這就是法國大數學家歐拉發現的著名的歐拉公式，在棱柱、棱錐頂點數（v）、面數（F）、棱數（E）內在聯系的探究過程中，教師引導學生從特殊到一般，從具體的數到字母，由數到式，發展了學生的抽象能力和推理能力，并在此過程中，將數與形緊密地結合了起來，

問題情境二：在小學三角形內角和1800的基礎上，讓學生操作、討論、探究，交流四邊形、五邊形、六邊形的內角和度數.由此深入，讓學生探究出n邊形的內角和與邊數n之間的關系：多邊形的內角和公式為（n-2）180°.

問題情境三：在n邊形內角和的基礎上，讓學生討論探究n邊形外角和的度數.學生們通過操作、討論交流，得出規律：n邊形外角和的度數為360°.

在猜想的基礎上，進一步引導學生加以推理，揭示其中的道理.多邊形的外角和360°可這樣推理得出：n邊形每個頂點處的內角與其一個外角的和為180°，而內角和為1800（n-2），這樣外角和為n180°-（n-2）180°=360°，通過推理，深挖其內在的規律和道理，

探究的過程充滿著神奇和樂趣，大干世界，多面體繁多，面數、頂點數和棱數卻有著神奇的內在聯系，這不能不讓學生對圖形世界產生好奇，不能不讓學生對數學產生濃厚的探究興趣.當學生通過自已的探究活動得出這些結論時，他們的欣喜之情溢于言表.對學生而言，他們的發現過程和數學家的發現過程一樣，都是一種創新，都一樣能體驗到數學學習的成功與快樂，這些不可思議的發現往往能給學生深刻的印象，正因為這節課，很多學生深深地喜歡上了數學、喜歡上了豐富的圖形世界.

讓我們領著學生走進豐富的圖形世界.從生活到圖片，讓學生多觀察周圍的世界，讓學生多發現生活中的物體；從圖片到圖形，讓學生從具體到抽象，從圖片中抽象出數學圖形，讓學生的思維經歷一個抽象的過程，引導學生用數學的眼光去看待這個豐富的圖形世界，這有助于學生形成正確的數學觀；從圖形到圖理，更是通過實踐探究、協作交流，引導學生透過豐富的數學圖形的表象，尋求其中蘊含的數學規律，這是數學學科教學的靈魂和價值所在.

教學是一門藝術.在教學中教師要思考和把握好三條“路”：一是教學思路，主要是指教學內容的設計，教學環節的把握和教學目標的設定；二是教師的教路，即教師教學時采用的教學方式和策略；三是學路，即學生的學習方式與策略，教學思路是課堂教學的路線、目標與方向，教路與學路是沿著適當路線實現目標所采用的工具、方式和方法，而其中教路往往會潛移默化地影響著學生的學路.如本節課中教師多采用探究、協作與交流的方法讓學生探究圖形規律，學生在后續學習中也就會自覺地運用這種操作、探究、交流的方法進行獨立學習.本節圖形課堂教學，“三路”清晰：思路就是從圖片到圖形再到圖理，由生活到數學，再由數學到數理，由表及里，由形象到抽象；教路是探究討論、發現交流；學路充分體現學生學習的自主性.學生主動參與探究、大膽交流、體驗成功.三者相互促進，相互融合，形成了一個教學整體.正因為思路、教路和學路的協調統一，讓本節課的教學更從容、更具特色.

數和形是數學這門課研究的主要對象.圖形的入門教學是這樣：遵循圖片一圖形一圖理的學習思路，由此我們不禁聯想起代數課的入門教學，我們同樣可以遵循：生活中的數據一數與式一數理的教學思路進行，在數與形的教學中，以形佐數，以數析形，數形結合，共同構建起學生的數學思維世界，endprint