數(shù)學教育與學生創(chuàng)新能力的培養(yǎng)

◆孟昭信

(山東省平陰縣第四中學)

數(shù)學教育與學生創(chuàng)新能力的培養(yǎng)

◆孟昭信

(山東省平陰縣第四中學)

培養(yǎng)學生的創(chuàng)新能力既是時代的需要，又是新課標的要求。面對新課程改革，積極探索，大膽實踐，勇于創(chuàng)新。下面就具體的數(shù)學教學過程如何培養(yǎng)學生的創(chuàng)新能力，談了幾點做法和體會，以供同仁借鑒。

數(shù)學教學 “創(chuàng)新教育” 創(chuàng)新能力

一、更新觀念，提高認識，做創(chuàng)新型教師

1.正確認識數(shù)學中的創(chuàng)新教育

“創(chuàng)新教育”是以培養(yǎng)人的創(chuàng)新精神和創(chuàng)新能力為基本價值取向的教育，其核心是創(chuàng)新能力的培養(yǎng)。從這個意義上理解，在數(shù)學教學中，通過對學生施以教育和影響，促使他們?nèi)フJ識數(shù)學領域的新發(fā)現(xiàn)、新思想、新方法等，掌握其一般規(guī)律，培養(yǎng)他們具有一定的數(shù)學能力，為將來成為創(chuàng)新型人才奠定數(shù)學素質(zhì)基礎。

2.克服對創(chuàng)新認識上的偏差

一提到創(chuàng)新教育，往往想到的是脫離教材的活動，如小制作、小發(fā)明等，或者是借助問題，讓學生任意去想去說，說得離奇，便是創(chuàng)新，走入了另一個極端。其實，每一個合乎情理的新發(fā)現(xiàn)，別出心裁的觀察角度等都是創(chuàng)新。所以，教師要讓學生掌握更多的方法，了解更多的知識，培養(yǎng)學生的創(chuàng)新能力。

3.做有創(chuàng)新精神的教師

數(shù)學教師自身要具備創(chuàng)新精神，這是數(shù)學教學中培養(yǎng)學生創(chuàng)新能力的一個重要因素。因此，應該充分調(diào)動教師的積極性和創(chuàng)新精神，努力提高創(chuàng)新能力，掌握更具有創(chuàng)新性、更靈活的教學方法，在教學實踐中，不斷探索和創(chuàng)新，不斷豐富和提高自己。

二、發(fā)揮課堂主渠道作用，強化創(chuàng)新意識，培養(yǎng)學生的創(chuàng)新能力

1.在教學數(shù)學知識時，通過有關(guān)的實際例子，說明數(shù)學在科學展中的作用，使學生認識學習數(shù)學的意義，鼓勵學生學習成才并積極參加數(shù)學實踐活動，激發(fā)學習數(shù)學的興趣和成就動機。這樣學生在接受教育和獲取知識的同時，形成推崇創(chuàng)新，追求創(chuàng)新，以創(chuàng)新為榮的觀念和意識。

2.啟發(fā)誘導，在課本例習題的變式訓練中培養(yǎng)學生創(chuàng)新能力的深刻性。在初中平面幾何的教學中，對課本上的例題或習題中的典型圖形進行一圖多變的訓練，有利于同學們加深對原題的理解與領會，從而激發(fā)學習興趣，啟迪思維，培養(yǎng)學生的創(chuàng)新意識和創(chuàng)新能力。

3.啟迪聯(lián)想，在開放題的探索中，培養(yǎng)學生創(chuàng)新能力的靈活性。開放題為學生的探索學習提供了更大的思考維數(shù)和思考自由度，拓寬了學習空間，在我講完邊角邊公理，角邊角公理及角角邊定理后，為了更好的靈活運用這三種判定方法，我設計了下面三道開放題：

(1)已知，在△ABC和△A′B′C′中，∠B=∠B′，BC=BC，當兩三角形再滿足一個什么條件時，△ABC≌△A′B′C′？

就具體策略而言，主要是實現(xiàn)“兩化”和“兩性”。所謂兩化，是指人民調(diào)解的“社會化”與“專職化”。所謂兩性，是指人民調(diào)解的“專業(yè)性”與“服務性”。

(2)已知，在△ABC和△A′B′C中，∠A=∠A′，∠B=∠B′，當兩三角形再滿足一個什么條件時，△ABC≌△A′B′C′？

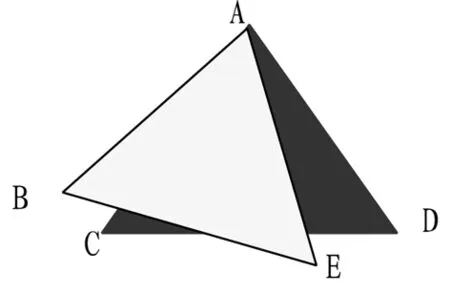
(3)已知：如圖，AB=AC，AD=AE，∠1=∠2，當△ACE繞點A旋轉(zhuǎn)任意角度時，△ABD和△ACE是否全等？

通過上述三道開放題的探索，學生真正理解掌握了三角形全等的三種判定方法，調(diào)動了學生的學習興趣和積極主動性，培養(yǎng)了學生創(chuàng)新能力的靈活性。

4.引導觀察，在實際問題轉(zhuǎn)化為數(shù)學問題的應用中，培養(yǎng)學生創(chuàng)新能力的敏捷性。

如圖，可以用兩根鋼條AA′和BB′，在中點O處連在一起做成的工具(卡鉗)測量工件內(nèi)槽的寬，按照圖寫出“已知”“求證”，并證明AA′=BB′。

此題，用沒有刻度的卡鉗測量內(nèi)槽的寬度，顯然不能直接讀出，但是通過教師的引導和學生的觀察，可以把此問題轉(zhuǎn)化為兩個三角形的全等，即證明△AOB≌△A′O′B′，從而根據(jù)全等三角形的性質(zhì)等到AB=AB。能以此題只要測量出A′B′的長度，就可得到AB即工件內(nèi)槽的寬。

5.師導生演，在某一題目解決的討論訓練中，培養(yǎng)學生創(chuàng)新能力的獨創(chuàng)性。

如解方程組：{x/3+3y=19①y/3+3x=11②

讓學生之間相互討論，尋求解決問題的方法，通過討論，得出以下三種解決法：

(1)原方程組化簡得：{x+9y=57③y+9x=33④再用代入法解；

(2)在思路(1)的基礎上進行整體相加得：10(X+Y)=90，即X+Y=9，再作整體代入④得9+8X=33，解得X=3，下略。

(3)①+②得10X/3+10Y/3=30，X+Y=9⑤。①-②得：8X/3-8Y/3=-8，X-Y=-3⑥，由⑤⑥可得X=3，Y=6。

顯然，(1)是常規(guī)解法，達到了數(shù)學中認識目標的要求：思路(2)具有整體思想和思維的靈活性；思路(3)具有知識的遷移和聯(lián)想能力，具有思維的深刻性。通過這種討論方式，學生心理愉快，興趣盎然，思路開闊。由于教師的因勢利導，大大培養(yǎng)了學生創(chuàng)新能力的獨創(chuàng)性。

總之，在數(shù)學素質(zhì)教學中，應根據(jù)數(shù)學學科的性質(zhì)和特點，數(shù)學教學的規(guī)律，針對當前中學生學習數(shù)學的實際情況，從學生創(chuàng)新精神培養(yǎng)的各個方面，來促進學生創(chuàng)新精神的形成和創(chuàng)新能力的提高。