帶Lvy過程的正倒向對偶系統隨機控制問題

冉啟康

(上海財經大學數學學院,上海　200433)

?

冉啟康

(上海財經大學數學學院,上海200433)

摘要：討論了一類控制系統是帶L′evy過程的正倒向對偶隨機微分方程的隨機控制問題.本文假定控制區域為凸集,最優解是使目標函數達到最小的控制過程.使用帶L′evy過程的It?o公式及Ekeland變分原理,作者建立了這類隨機控制問題極值原理的一個必要條件.

關鍵詞：正倒向對偶隨機微分方程;隨機控制問題;變分不等式;極值原理; It?o公式

1　引言

自1990年Pardoux與彭實戈在文獻[1]中首先證明了由標準Brown運動驅動的非線性倒向隨機微分方程適應解的存在唯一性以來,由于倒向隨機微分方程在控制論、金融數學、偏微分方程理論等眾多學科中有著廣泛的應用而引起了許多科學工作者的重視,到目前為止,相關的文獻數不勝數. 1994年,文獻[2]中引入了倒向對偶隨機微分方程,即方程包含兩個隨機積分,一個是標準的隨機積分一個是倒向隨機積分證明了當系數滿足一致Lipschitz條件時,方程

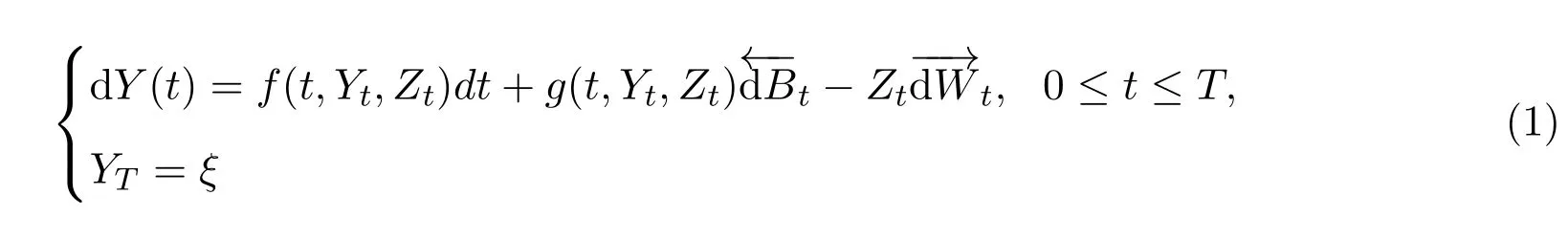
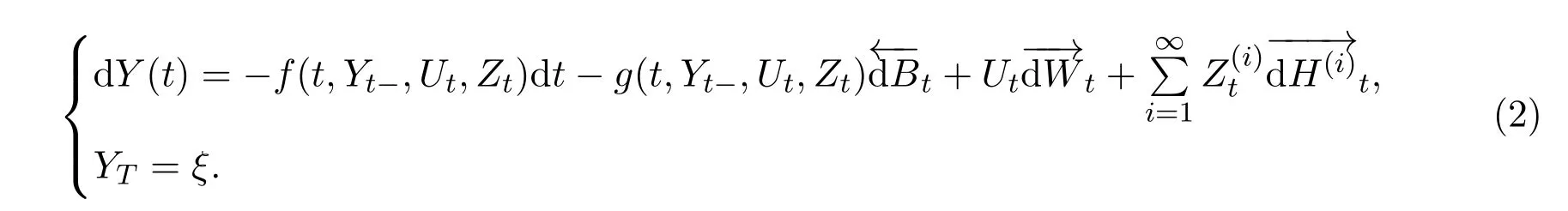
證明了當系數滿足一致Lipschitz條件時,方程存在唯一的適應解.控制系統是一個正倒向隨機系統的隨機控制問題最先是彭實戈在文獻[4]中提出的,在控制區域是凸集的條件下,建立了一個極值原理由.之后,大量的結果不斷出現[5-9].最近,文獻[10]中討論了控制系統為:

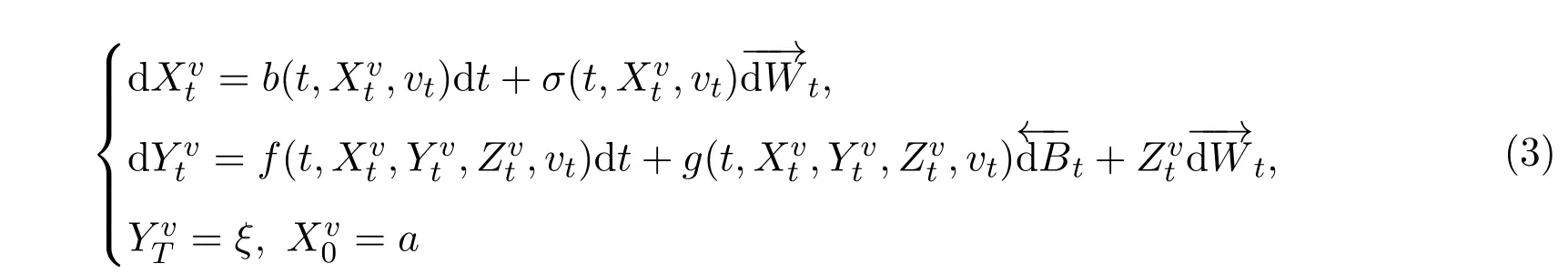
的隨機控制問題,建立了一個極值原理的必要條件.本文是文獻[10]的推廣,利用文獻[3]的結論,借鑒文獻[10]的主法,建立了一類控制系統是帶L′evy過程的正倒向對偶隨機微分方程的隨機控制問題,建立了這類控制問題的極值原理的一個必要條件.

2　預備知識及引理

首設T是一個正常數, (?,F,P)是一個完備的概率空間,

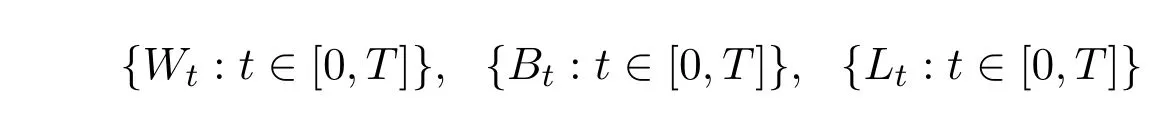
是三個相互獨立的過程,其中, {Wt: t∈[0,T]}與{Bt: t∈[0,T]}是兩個一維標準Brown運動, {Lt: t∈[0,T]}是一維右連左極L′evy過程,滿足: Lt= bt + bt, {bt}的跳時間是不可達停時; Lt對應的標準L′evy測度ν滿足下列條件:

2)對所有ε＞0和某個λ＞0,有

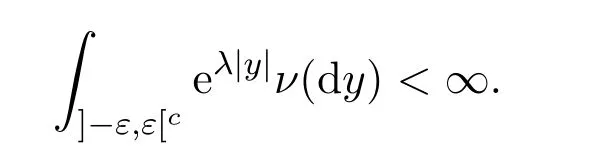
記

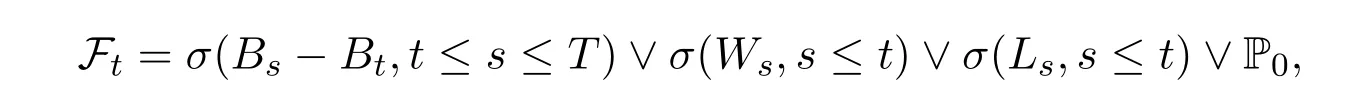
其中P0表示P-零測集全體, G1∨G2表示由G1∪G2生成的σ-代數.顯然{Ft,0≤t≤T}不滿足通常性條件,因為它既不單調增加,又不單調減少.設(H(i))i≥1是由{Lt: t∈[0,T]}生成的Teugel鞅,即

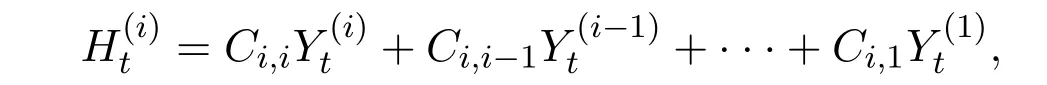
其中

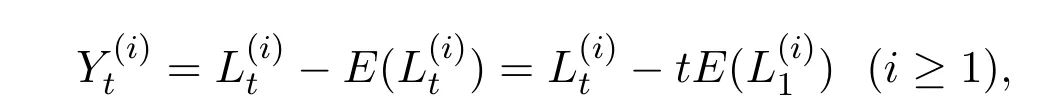
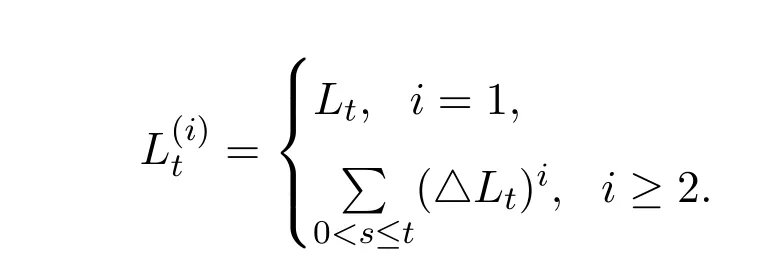
由文獻[11]知, (H(i))i≥1的分量是兩兩正交的,且[H(i),H(j)]t=δijt.

下面,引入文中所需的正向或倒向SDE的解空間.

(1) H2的元素Z :?×[0,T]→R,滿足:

(i)

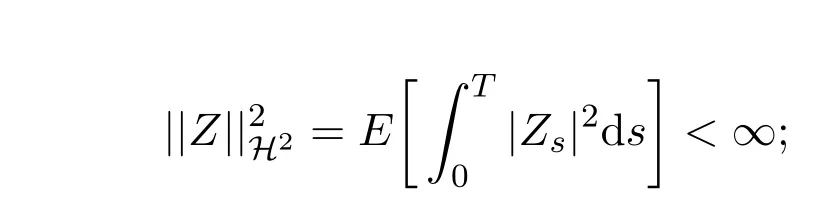
(ii)?t∈[0,T], Zt是Ft可測的.用M2表示H2中的可料過程構成的子空間.

(2) S2的元素Y :?×[0,T]→R,滿足:

(i)

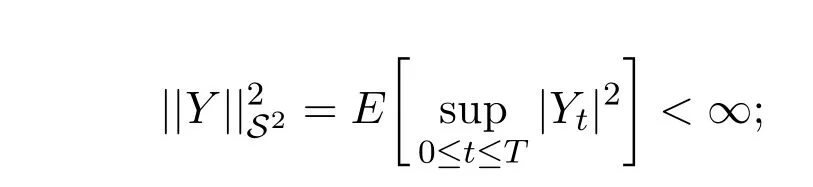
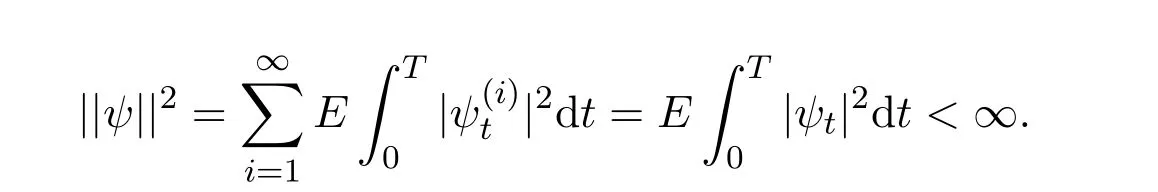
定義2.1設U是R中的非空凸子集,稱Ft-適應過程v為一個容許控制,如果它滿足:

(i) v的值在U中;

本文中,控制系統是下列正倒向對偶隨機微分方程組:

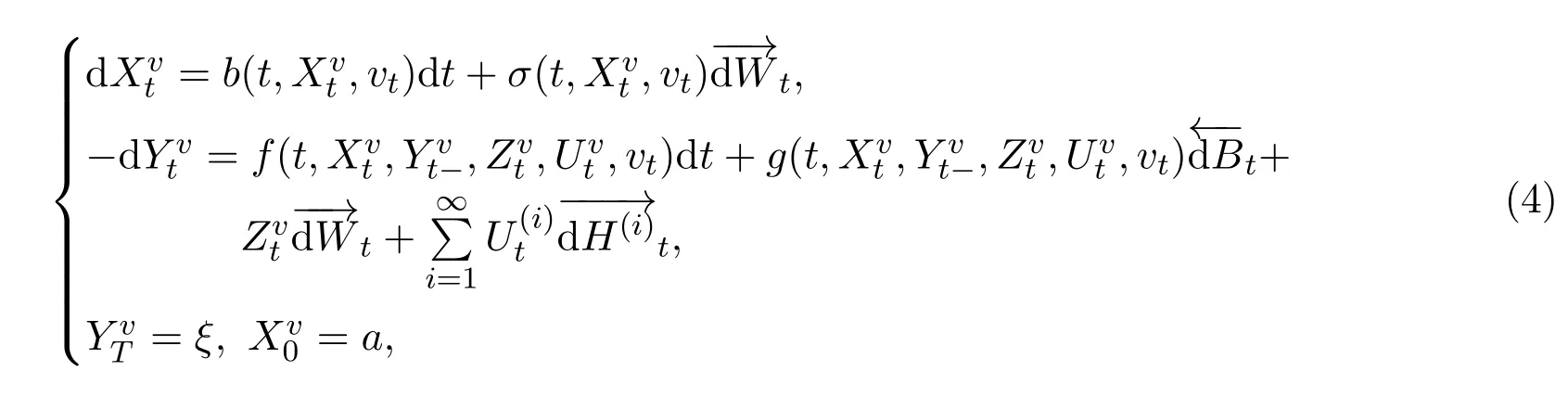
為了記號簡單,在余下的部分,將省去積分的箭頭.

定義2.2對任意給定的v∈U,稱(Xv,Yv,Zv,Uv)為方程(5)對應于v的解,如果(Xv,Yv,Zv,Uv)∈S2×S2×M2×M2(l),且滿足方程(5).

定義2.3稱u∈U為最優控制,如果它使成本函數

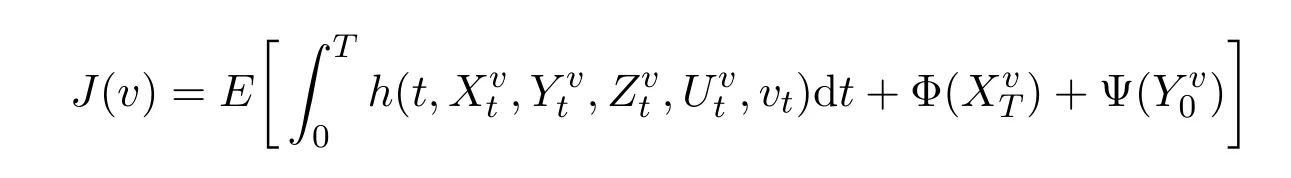
達到最小值,即

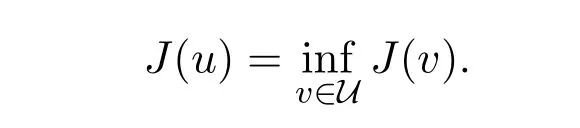
假設函數f(t,x,y,z,u,v), g(t,x,y,z,u,v), b(t,x,v),σ(t,x,v), h(t,x,y,z,u,v),Φ(x),Ψ(y)滿足下列條件:

(H1)所有函數關于(x,y,z,u)都是連續可微的,關于t∈[0,T]是可測的.

(H3)

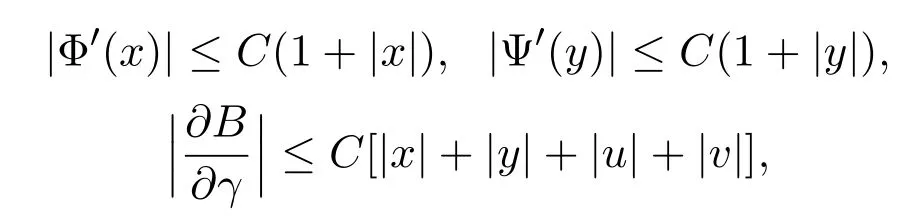
其中, B表示b,σ, h中任一函數,γ表示x,y,z,u,v中任一變量.

為了引入本文的主要結論,首先引入兩個引理,它們是由文獻[10]中相應引理推廣而來.設u?是一個最優控制是對應的最優策略.設因為U是凸的,所以,?0≤p≤1,有為下列正倒向對偶SDE的唯一解:

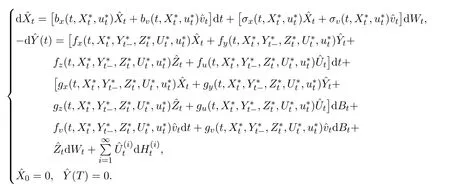
設(Xp,Yp,Zp,Up)為方程(5)中v = up對應的解,記

則有

引理2.1假定條件(H1)- (H3)成立.那么

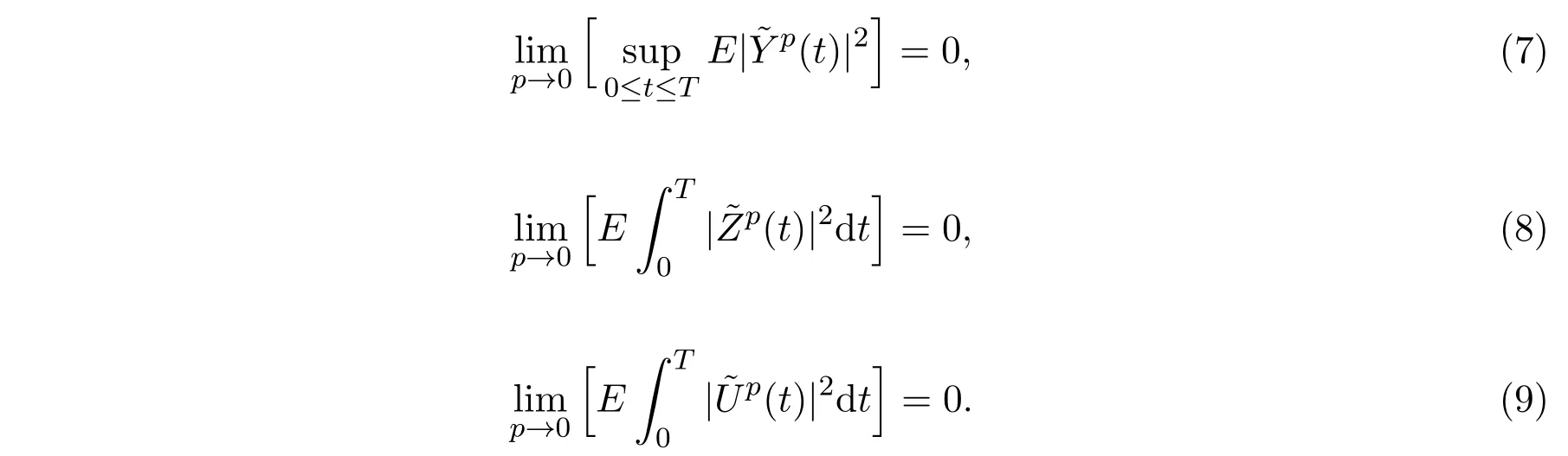
證明由文獻[12]中引理4.1知, (7)式成立.因為

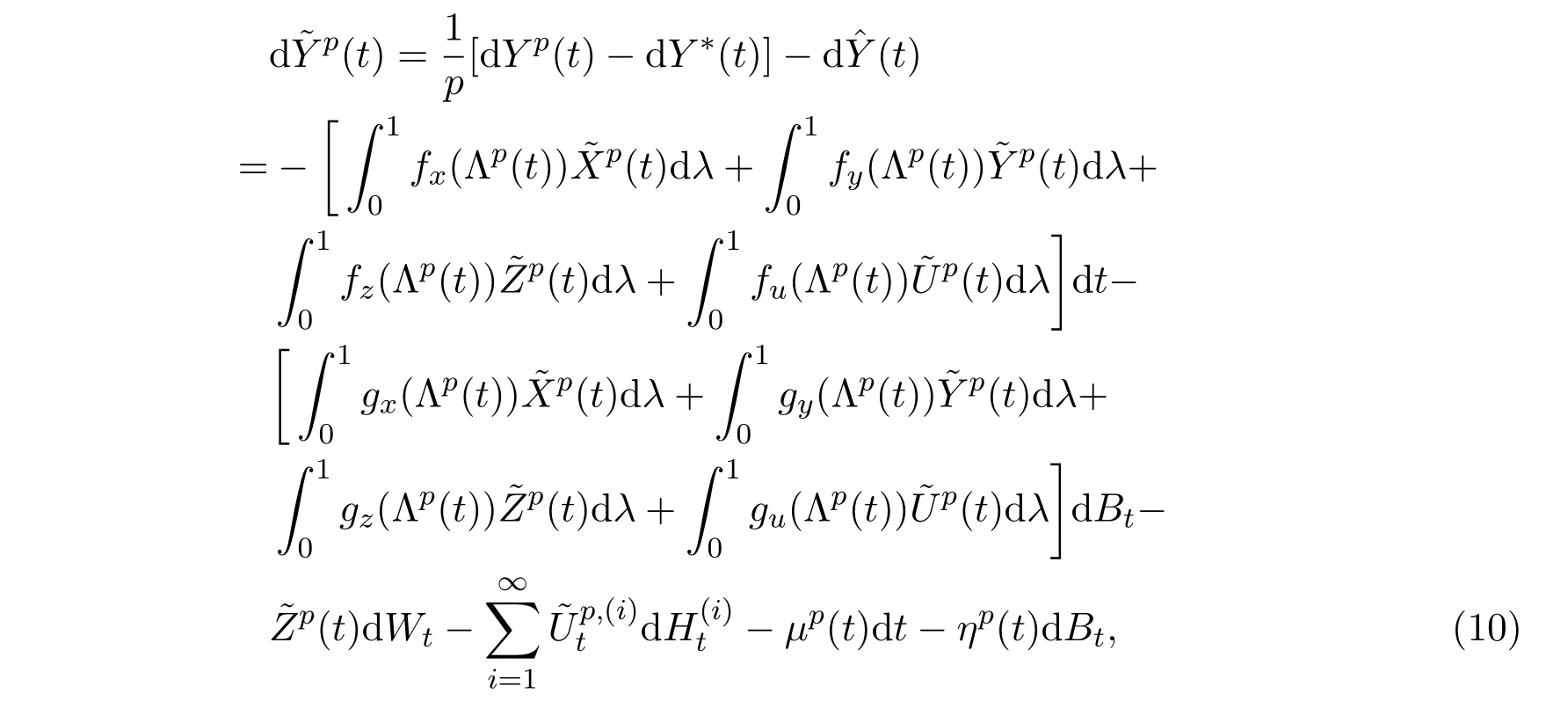
其中

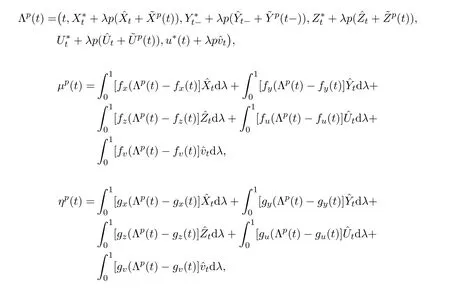
此處及以后,均用fx(t)表示其他函數也用同樣的表示.

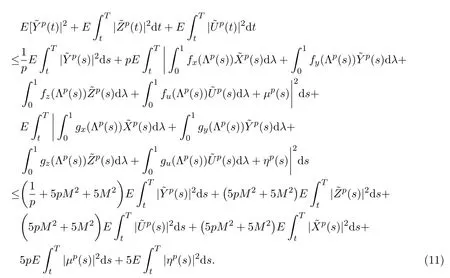
類似于文獻[10],有

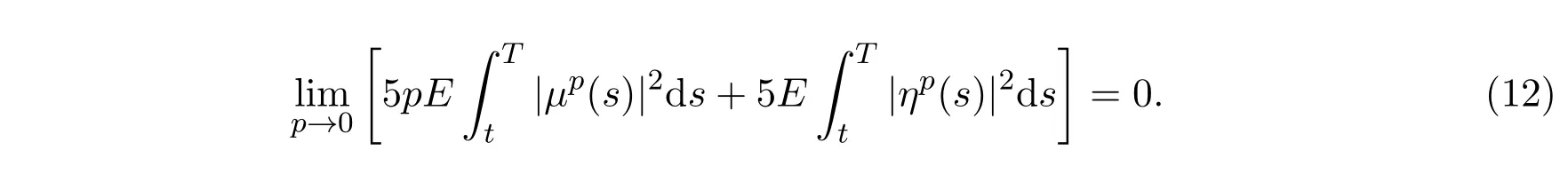
由引理2.1可得下列結論:

引理2.2假定條件(H1)-(H3)成立.如果u?是最優控制,那么下列變分不等式成立:

證明使用引理2.1,與文獻[10]中引理2.5完全類似,可得引理2.2結論成立.

3　主要結論及證明

定理3.1假定條件(H1)-(H3)成立.如果u?是最優控制, (X?,Y?,Z?,U?)是對應的最優策略,那么,對任意v∈U,必有

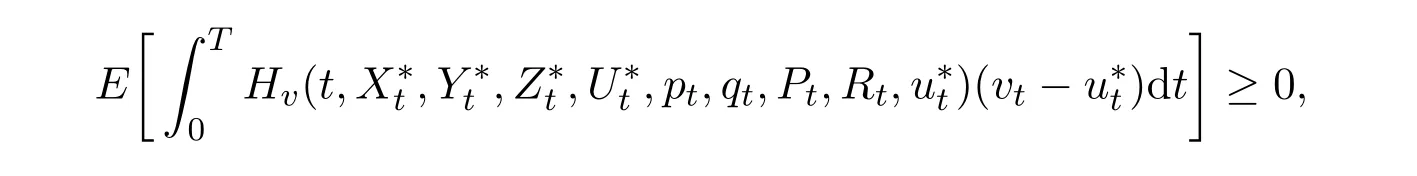
其中

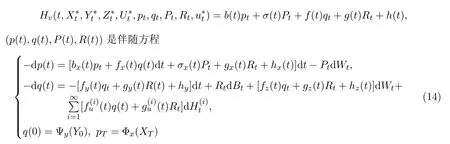
的解.

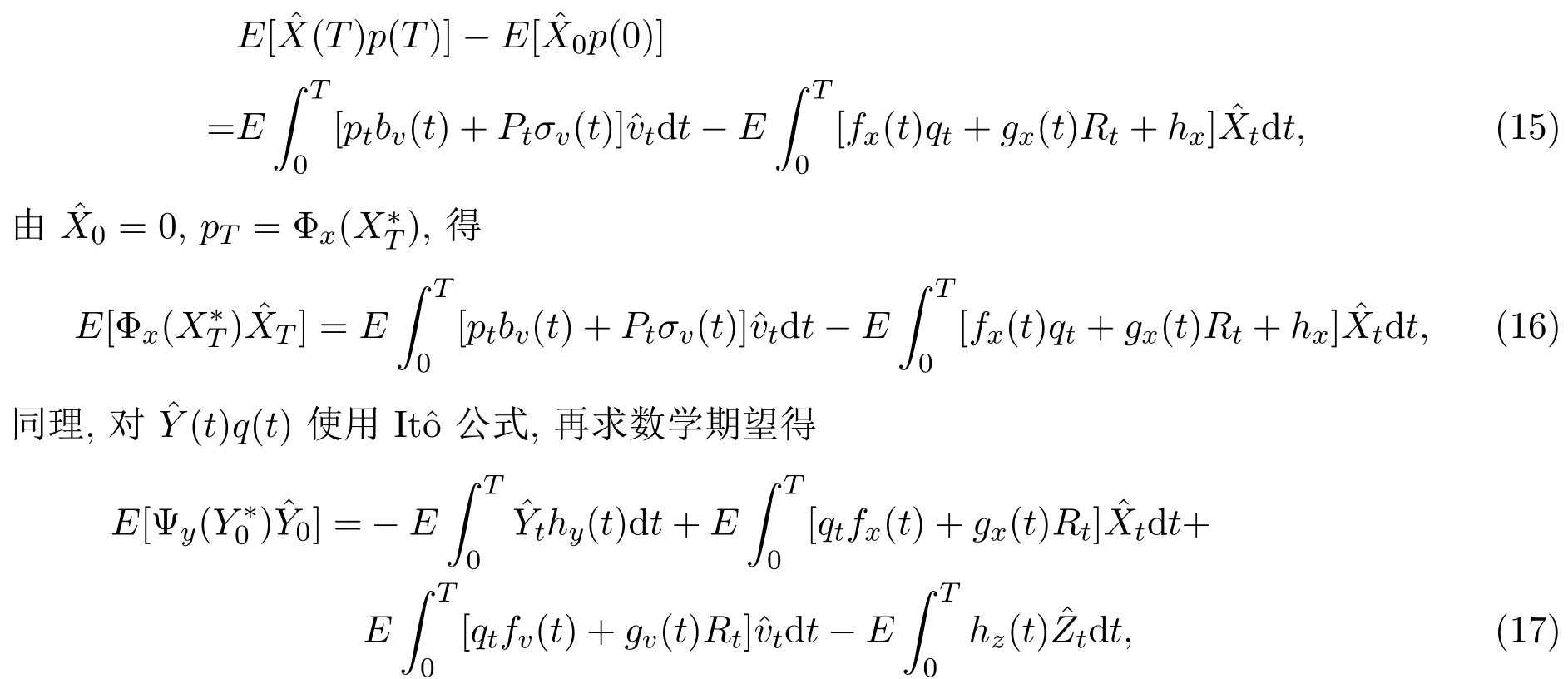
將(16), (17)式代入(14)式,得

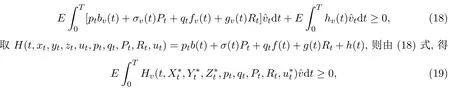
在(19)式中取?v = v?u?立即得定理3.1的結論成立.

參考文獻

[1] Pardoux E, Peng S. Adapted solution of a backward stochastic differential equation [J]．System Control Lett., 1990,14:55-61.

[2] Pardoux E, Peng S. Backward doubly stochastic differential equations and systems of quasilinear SPEDs [J]. Probab. Theory Related Fields, 1994,88:209-227.

[3] Yong Ren, Aihong Lin, Lanying Hu. Stochastic PDIEs and backward doubly stochastic differential equations driven by L′evy processes [J]. Journal of Computational and Applied Mathematics, 2009,223:901-907.

[4] Peng S. Backward stochastic differential equations and application to optimal control [J]. Appl. Math. Optim., 1993,27:125-144.

[5] Xu W. Stochastic Maximum principle for control problem of forward-backward system [J]. J. Aust. Math. Soc. Ser., B, 1995,37:172-185.

[6] Wu Z. Maximum principle for optimal control problem of fully coupled forward-backward stochastic control system [J]. Syst. Sci. Math. Sci., 1998,11(3):249-259.

[7] Biagini F, Hu Y Z,?ksendal B, et al. A stochastic maximum principle for processes driven by fractional Brownian motion [J]. Stochastic Processes and their applications, 2002,100(1):233-253.

[8] Ji S, Zhou X Y. A maximum principle for stochastic optimal control with terminal state constraints and its applications [J]. Commun. Inf. Syst., 2006,6(4):321-338.

[9] Ji Shaolin, Wu Zhen. The maximum principle for one kind of stochastic optimization problem and application in dynamic measure of risk [DB/OL].(2007-12-04) [2015-7-15]. http://www.paper.edu.cn.

[10] Adel Chala. Necessary condition for optimality of forward-backward doubly system[J]. Afr. Mat., 2015,26:575-584.

[11] Nualart D, Schoutens W. Chaotic and predictable representations for L′evy processes [J]. Stoc. Proc. Appl., 2000,90(1):109-122.

[12] Bensoussan A. Lectures on stochastic control [C]// Proceedings in Nonlinear Filtering and Stochastic Control. New York: Springer-Verlag, 1981.

2010 MSC: 60H10, 93E20

The stochastic control problem for forward-backward doubly system with L′evy processes

Ran Qikang
(School of Mathematics, Shanghai University of Finance and Economics, Shanghai 200433, China)

Abstract:In this paper, we discuss a class of stochastic control problem whose control system is a forwardbackward doubly stochastic differential equations system. We assume the control domain is convex and the optimum solution is to minimize the objective function. We prove a necessary condition of maximum principle for this class of stochastic optimization problem , by using It?o formula of L′evy processes and Ekeland variational principle.

Key words:forward-backward doubly stochastic differential equation, stochastic control problem, variational inequation, the maximum principle, It^o formula

作者簡介：冉啟康(1964-),博士,教授,研究方向：隨機分析、金融數學.

收稿日期：2015-08-28.

DOI：10.3969/j.issn.1008-5513.2016.01.002

中圖分類號：O211.63

文獻標識碼：A

文章編號：1008-5513(2016)01-0006-08