《新課標》與《義教版》分數應用題教學異同的實踐與研究

諸葛軍

【摘要】本人執教六年級多年，今年第一次使用《新課標》教材，對學生進行“用分數解決問題”教學時很發現教學效果很差，聯想到兩年之內教師還是同一個教師，學生也是同齡的學生，唯一改變的是材。所以筆者試著對《新課標》和《義教版》兩種教材進行比較分析，發現這兩種教材對分數應用題的編排有較大的差異，從而提出在《新課示》的教材下教學“用分數解決問題”的策略。

【關鍵詞】《新課標》 《義教版》 “分數解決問題” “分數應用題”

【中圖分類號】G62 【文獻標識碼】A 【文章編號】2095-3089（2016）03-0023-03

一、問題的提出

在教學用百分數解決問題（新課標P90例2）時，“例2題目如下：我們原計劃造林12公頃，實際造林14公頃，實際造林比計劃增加百分之幾？”我設想的教學思路是：第一步由分數的簡單三類應用題引入，準備題三道①原計劃造林120公頃，實際造林是原計劃的4/5，實際造林多少公頃？②實際造林120公頃，是原計劃的4/5，原計劃造林多少公頃？③原計劃造林120公頃，實際造林100公頃，實際造林是原計劃的幾分之幾？第二步將分數改成百分數，接著重點教學第三類應用題，從而求讓學生回憶求一個數是另一個數的幾分之幾（百分之幾）的應用題的關鍵在于找出哪兩個量相比，第三步引到本節課求一個數比另一個數多（少）百分之幾的應用題，也在于找出哪兩個量相比，只不過要用多（少）的量和單位“1”相比。

課堂教學片斷：

準備題練習五分鐘后，師：已經做好的請舉手。

生反應：舉手的同學寥寥無幾。

教師耐著性子再等了片刻，舉手的還是那么幾位同學，和原來相差無幾。

教師循回檢查，發現學生解答①②兩題的正確率不超過50%。

于是筆者只好調整教學思路，將準備題當著練習課來教學，當教師告訴學生求一個數的幾分之幾是多少用乘法時，一位平時成績還較好的女學生怯怯地問了我一句：“老師，為什么求一個數的幾分幾是多少用乘法？”，聽到這一問話，我當時驚呆了，這是最基本的東西，也是第二單元學習的一個重點，這位學生的問話，讓人感覺是：這位女生好像從來沒有學過分數應用題似的，好像今天是第一節剛接觸應用題，（但現實是：用分數解決問題的教學已接近尾聲，剩下的教學只不過是百分數的應用而已，而且這還是平時表現比較好的一位女生）分數應用題還是停留在這樣的理解基礎上，也難怪學生不能正確解答①②類應用題。

二、原因的分析

課后分析：這種情況的出現主要是這幾個原因造成的，第一、學生當初在學習“用分數解決問題”時根本就沒有很好的掌握這一知識。第二，學生的知識出現了遺忘，而③題正確率較高的原因是由于這段時間學生正在學習百分數的意義和百分率應用題。

再進一步思考，兩年前我還是我，學生也是同齡的學生，兩年前利用《義教版》教材進行分數應用題教學時一直比較順利，根本就沒有出現過這樣的問題，兩年后怎么反差如此之大。從而讓人想聯，這樣的問題的出現是不是與新課標的教材有關，筆者用了一個星期的時間將《義教版》教材和《新課標》教材進行了比較，結果發現如下：

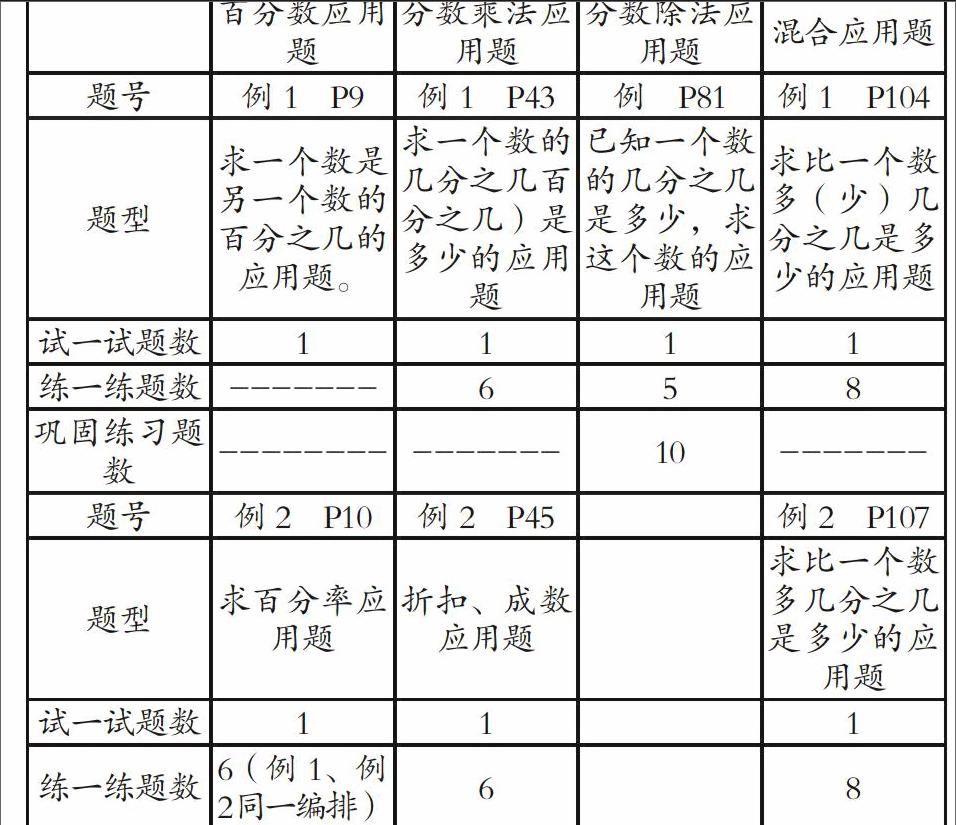
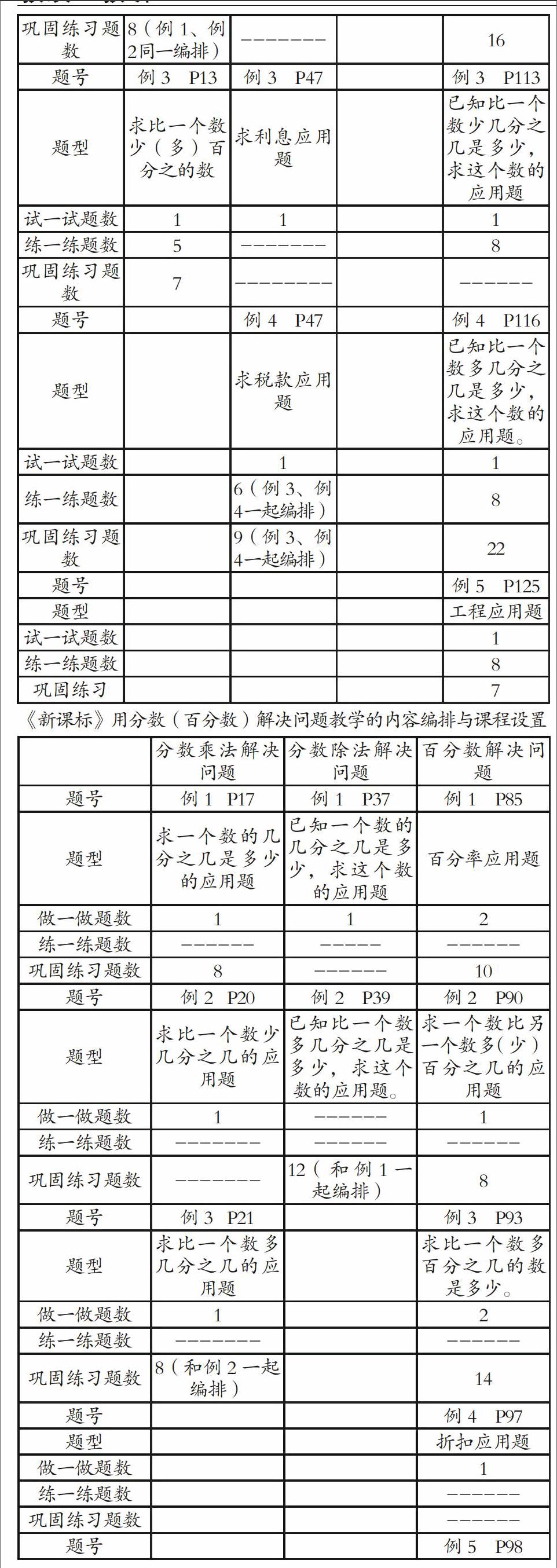
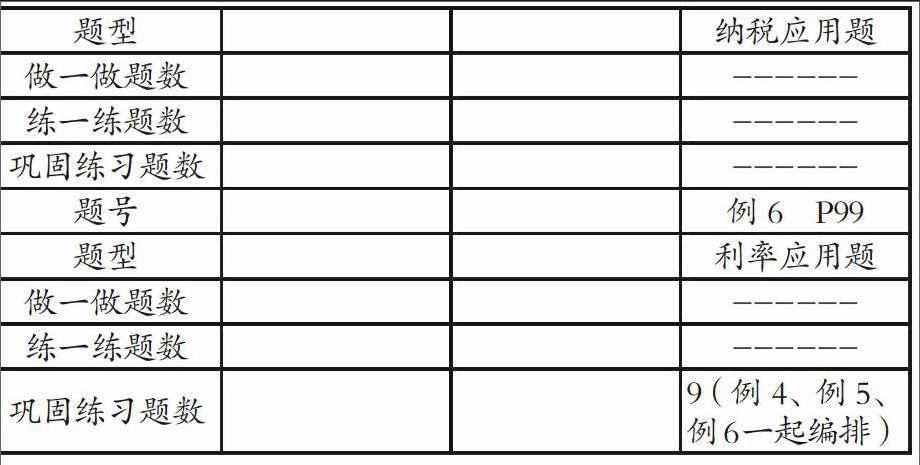
《義教版》和《新課標》編排的不同點：

1.數量上比較，義教版這部分應用題共29+31+16+90=166道，新課程共19+13+47=69道，《新課程》從題目數量編排來看，練習題比《義教版》少了一半多，這對于學生技能的形成就少了一道工序。俗話說：“勤能補拙”，作業練習題的減少，這對于還處于形象思維向邏輯思維轉化、理解力本來就較差的六年級學生來說，掌握這一類應用題就增加了難度。

2.編排秩序比較，《義教版》先出現的是百分數應用題，再出現分數乘除應用題，最后出現稍復雜的分數乘除混合應用題。體現了一種由易到難的課程編排理念，比較適合學生的認知規律，掌握起來經比較容易。而《新課程》內容編排以應用為理念，學以致用，學到分數乘法就編入用分數乘法解決問題，進行百分數教學時就編入用百分數解決問題。但這樣一來，解決問題的難易度就受到了影響，因為用百分數解決問題相對更容易一些，諸如象稅率、利率單位“1”的量是已知的，而分數應用題的真正難點在于求單位“1”的應用題。所以難點應該是第二單元分數除法應用題，這樣一來難點就靠前，學生掌握這一部分知識就比較累，正因為這一部分知識沒有掌握到位，自然也影響到了后一單元“用百分數解決問題”。

3.難點編排比較，《義教版》的分數應用題的難點是放在第四單元（分數、小數四則運算和應用題）在這一單元里，《義教版》教材前后共安排了90道應用題，這對于學生辨析、區分、理解分數應用題無異有極大的幫助。而《新課標》的難點不是很明確。

三、《新課標》“用分數解決問題教學”的教學策略

策略（一）充分理解分數應用題的內涵和外延。

在進行第二單元（分數乘法）教學時，學生比較容易接受，正確率較高，但學生是否真正理確單位“1”的量，又是另外一回事，所以在進行這一教學環節時，一定要引導學生充分認識單位“1”，要以分析理解為前提，不以學生的作業正確率為唯一指標。讓學生真正知道一個數的幾分之幾的外延和內涵。

策略（二）尋找解答分數應用題的最佳方法。

1.化抽象文字為表象圖例。在教學例2“美術興趣小組有25人，比航模小組多1/4，航模小組多少人？”時，我將教學的重點放在幫助學生理解“比航模小組增加1/4”，在這基礎上構畫出兩者的倍比關系線段圖：

有了這樣的倍比關系線段圖就將原先的抽象文字符號轉化成直觀形象的圖示。這就給解決分數應用題給了很大方便，所以當教師再將已知條件和問題標出后，學生大多能正確計算；

2.優化分數應用題學習的過程。我們學校今年在數學應用題教學時采用了“三想教學法”。一想把誰看成單位“1”；二想數量關系是什么；三想怎樣列式；如上段中例2的解題思路為：根據“航模小組增加1/4”把航模小組看作單位“1”（一想）。根據“航模小組增加1/4”轉化為航模小組是美術小組的（1+1/4）（二想）。再根據乘法的意義列出方程式或算式（三想）。這種解答思路比較明確，學生比較容易掌握，并運用了對應、轉化和代數的數學思想和方法，降低了思維的坡度，對于邏輯思維較差的小學生提供了解題方便。

3.“口訣”明確化。對于思維遲緩的學生則贈送兩看口訣“看看單位1，確定乘與除，看看多和少，決定加與減”。有了這兩句口訣，思維遲緩的學生也能根據口訣進行仿練，經過長期的訓練，這類學生也能掌握分數應用題的解題方法。

策略（三）反復強化，形成動力定型。

巴甫洛夫的“經典條件反射說”和斯金納的“操作性條件反射說”都將反射和強化作為學習的一個必要過程。斯金納認為，人和動物的學習行為主要是由操作條件反射構成的，他認為行為之所以發生變化是由于強化作用，強化是塑造行為的有效而重要的條件，所以學生在學生某一個知識點時要及時的“反饋”和強化，從而將這一知識點落到實處（經強化學生能每次都做出正確的反應，使錯誤率降低限度）。本人認為在進行《新課標》的“用分數解決問題”的教學時，要做好三個強化，第一個強化用在剛進行“用分數解決問題”教學時，這一階段可以適當增加題目量。（除了《新課標》課本上的習題之外，教師可以自編題目讓學生進行練習，最方便最有效的方法是將原來的《義教版》的課本中的題目進行利用） 第二個強化則分解在平時常規的課堂教學中，在平時教學中適時的出幾道分數應用題，對這方面知識進化強化。 第三個強化用在進行百分數解決問題教學前，因為這一階段的教學和“用分數解決問題”是斷檔的，中間穿插了《圓的認識》教學，對于記憶力差的學生來說，分數應用題已經開始遺忘了，所以在這個時候進行一次完整的分數三類應用題的強化。

參考文獻：

[1]邱少華.解應用題的鑰匙[M]. 江蘇：江蘇人民出版.

[2]朱智賢.兒童心理學[M]. 北京：人民教育出版社.

[3]童祥禎.小學數學課堂教學藝術[M]. 北京： 首都師范大學出版社.

[4]程功，陳仙梅.教育心理學[M]. 杭州：浙江大學出版社.