以電流矢量為目標的永磁同步電機定子電流動態預測

荊 鍇孫鶴旭,2董 硯鄭 易

（1.河北工業大學控制科學與工程學院 天津 300130 2.河北科技大學 石家莊 050018）

?

以電流矢量為目標的永磁同步電機定子電流動態預測

荊 鍇1孫鶴旭1,2董 硯1鄭 易1

（1.河北工業大學控制科學與工程學院 天津 300130 2.河北科技大學 石家莊 050018）

摘要提出一種以電流矢量為目標的永磁同步電機（PMSM）定子電流動態預測方法。通過研究αβ靜止坐標系下PMSM定子電流矢量動態響應，得出電流矢量變化的三個作用分量，并在離散周期上，利用泰勒級數對每個分量截斷近似，進而得到PMSM定子電流矢量的動態預測方法。對方法中各個分量的近似誤差進行了分析，同時為參數選擇和應用條件提供了理論依據。最后，利用實驗驗證了預測方法的準確性。

關鍵詞：永磁同步電機 電流矢量 電流預測 誤差分析

河北省重大科技成果轉化項目（13041709Z）和河北省自然科學基金（E2013202108）資助項目。

0 引言

永磁同步電機（Permanent Magnet Synchronous Motor,PMSM）具有高效率和高功率密度等特點，由PMSM構成的電機系統越來越多地應用在兵工和工業等領域的高性能伺服系統中。電機電磁轉矩響應的快速性和穩定性是保證交流伺服系統動態性能的關鍵，而與電磁轉矩直接相關的電流環性能則成為反映伺服系統性能的重要指標。

預測控制[1-3]具有較高的動態響應性能，能夠實現快速跟蹤，在定子電流跟蹤的數字調節中具有較佳的性能。該方法通常是利用當前時刻的采樣值和狀態值，預測電流變化趨勢，給出最佳的輸出控制量。其中，電流變化趨勢的預測過程是預測控制的關鍵，電流預測結果是否準確直接影響控制技術的復雜與否以及控制結果的優劣。對此，國內外學者進行了大量的研究。文獻[4]分析了電流在每一個開關狀態下的變化斜率，從而總結規律得到電流預測方法。文獻[5]設計了前饋-反饋控制器對電流進行預測和控制。文獻[6]對PMSM定子電流方程進行離散近似處理，并通過引入權重因子，得出具有魯棒控制性能的電流方程，然而未給出反電動勢的作用以及高速運行時的具體補償措施。文獻[7]結合無差拍控制思想，引入龍伯格觀測器對電流進行預測。上述研究均建立在已有的預測算法上，沒有對電流的動態響應進行分析，而且算法比較復雜，對反電動勢所帶來的電流變化分析不深入，未能全面反映電流的變化規律，預測準確度不高。此外，上述大多數研究均是基于轉子磁鏈的dq旋轉坐標，針對id、iq單獨進行預測和控制，因dq電流存在耦合，一些方法致力于方程的解耦控制[8,9]，一些方法則將耦合項直接忽略[6]。這些方法是對id、iq以獨立變量形式單獨計算和調節的，沒有將電流以矢量的形式看作整體進行預測和控制，而且dq坐標下并不能直觀地反映三相電流的實際動態變化。

本文將在αβ靜止坐標系下，以電流矢量為目標，將電流矢量的動態響應分解為三個獨立的變化分量，根據各個分解矢量的表達式，利用泰勒級數，將連續的動態變化離散近似到控制周期上，從而得出電流矢量動態變化的預測方程。文中對近似產生的截斷誤差進行分析，尤其是對電機反電動勢產生的電流變化矢量，給出矢量誤差的輪廓線圖，為相關參數的選取以及方法的應用條件等提供了理論依據。最后，通過仿真以及電機平臺實驗，對電流矢量的預測控制進行實際測試，得到了很好的電流預測效果。

1 PMSM模型及電流矢量的動態變化分量

PMSM在dq同步旋轉坐標系中的電機“電壓-電流”方程為

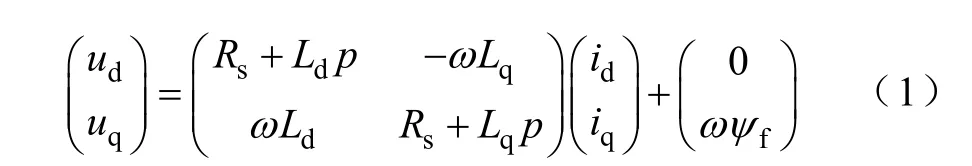
式中，Rs為定子電阻；Ld、Lq分別為d、q軸定子電感；ud、uq分別為d、q軸定子電壓分量；id、iq分別為d、q軸定子電流分量；ψf為轉子磁鏈；ω 為轉子電角速度；p為微分算子。

對于隱極式PMSM，有Ld＝Lq＝Ls，利用“旋轉-靜止”坐標變換，令轉子相對于A相軸線方向即α軸的位置為θ，則式（1）變換到αβ 坐標、并寫成定子電流矢量的狀態空間表達式為

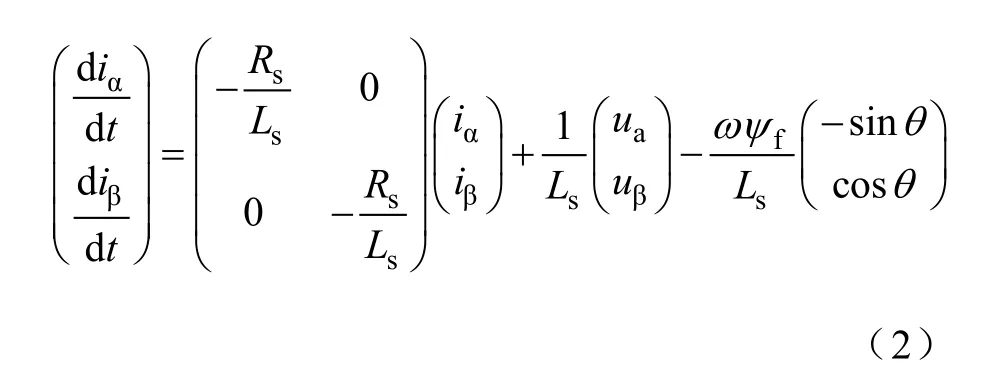
式中，iα、iβ分別為定子電流矢量is的α、β 軸電流分量；uα、uβ分別為定子電壓矢量us的α、β 軸的分量。設初始時刻為t0，經過足夠短的時間t，其間可認為電角速度ω 恒定，且有θ ＝θ0＋ωt，θ0為t0時刻轉子的電角度；電壓矢量，認為是在t時間內施加電壓的平均值，其與直流母線電壓Udc以及開關管狀態之間的轉換關系參見文獻[10]。通過求解狀態方程，得到電流矢量is的通解形式為

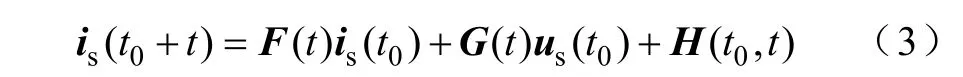
其中

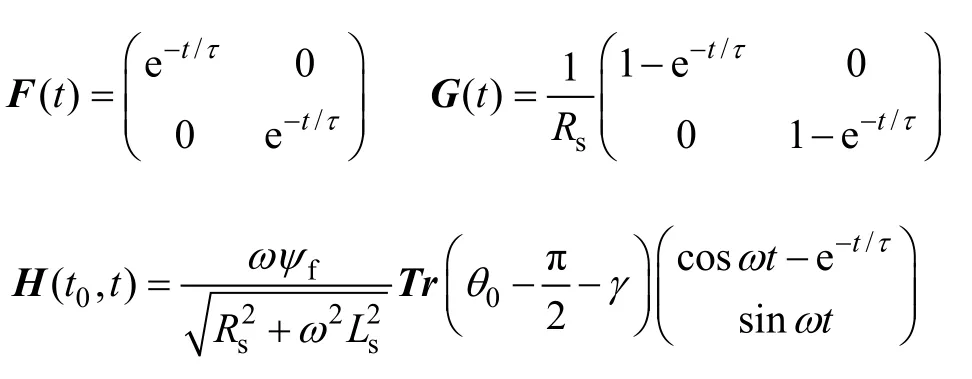
式中，τ為電機時間常數，τ＝Ls/Rs；γ＝ arctan（ωLs/Rs），是銳角；Tr（·）為逆時針旋轉變換矩陣，式（3）反映了時間t內PMSM電流矢量的動態響應。如果取電流矢量變化量為

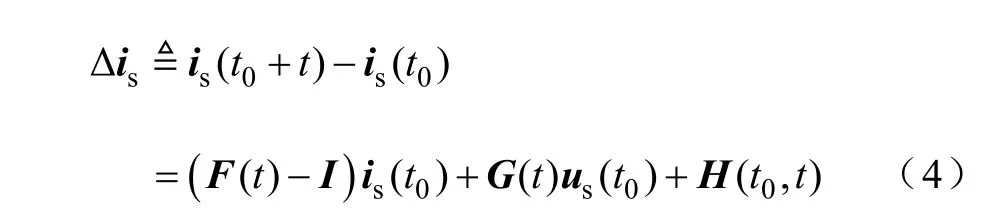
式中，引起電流矢量變化的量為初始電流矢量、輸入電壓矢量以及轉速（反電動勢矢量），三者對電流變化的作用無耦合關系，并滿足電路的疊加定理，分別記為Δisi、Δisu和Δisω，則

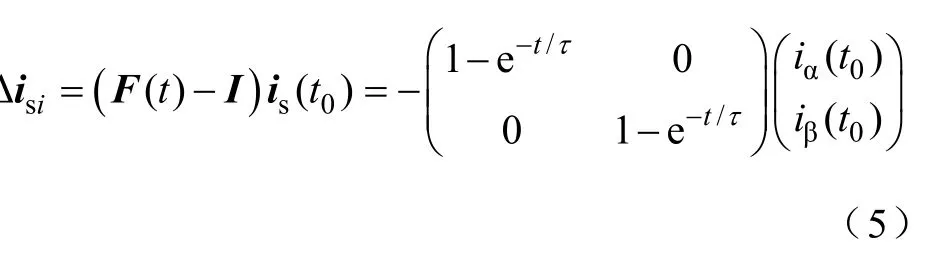
Δ

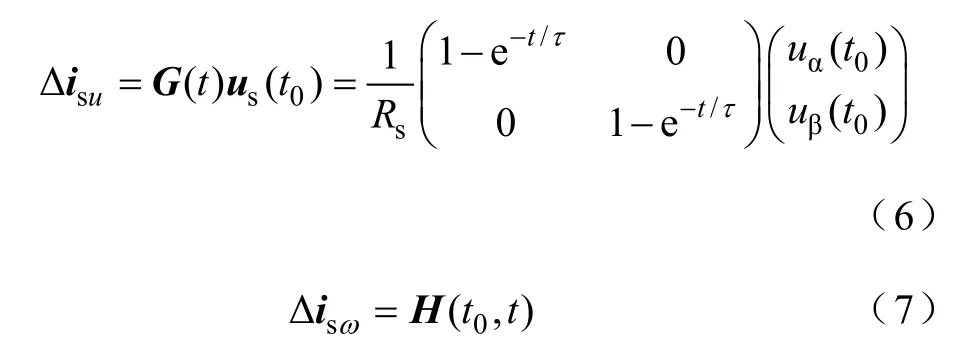
則PMSM電流變化矢量分解為三個獨立的動態變化分量。三者獨立作用時的響應過程分別如圖1中實線和虛線所示，其中和∠Δi分別為電流矢量變化量幅值和相位。

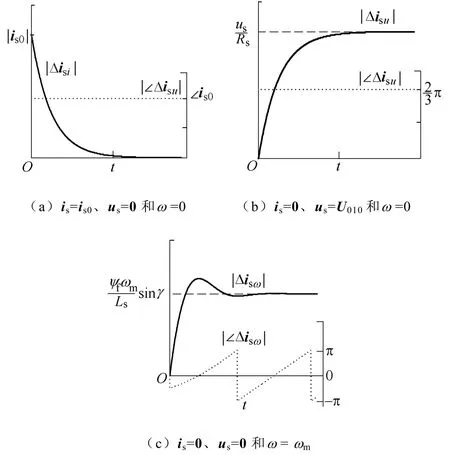
圖1　電流矢量三個分量的獨立響應曲線Fig.1 Response curve of the three components of current vector

由圖1a可知，Δisi使電流矢量的幅值按指數規律衰減；由圖1b可知，Δisu在外加電壓矢量方向上使電流矢量幅值呈指數增長；由圖1c可知，Δisω方向隨轉子位置變化，幅值形似二階阻尼系統響應的變化，其中，低速時可近似忽略Δisω的作用，當速度較高時，分析電流矢量變化需考慮該矢量的幅值和相位的影響。

2 基于電流矢量動態響應的PMSM電流預測方法

2.1 電流矢量的動態預測

在PMSM的離散數字控制系統中，獲得的電流和轉速等均為離散采樣值，取控制周期與采樣周期同步，典型的電機電流數字控制時序為：按k-1時刻的采樣值和給定值，計算當前時刻需要輸出的控制量，在k時刻輸出控制量，到k＋1時刻方可知道電流控制結果是否能跟隨，可見，電流的跟蹤延時至少為兩個控制周期[11]。采用電流預測的方法，則可以減小因控制周期的延時帶來的跟蹤波動，在k-1時刻可以利用采樣值預測k時刻的電流值，從而提前一個周期計算控制量。為實現電流跟蹤的穩定，需要預測計算有較高的準確性。

基于式（4），將其分量表達式（5）～式（7）中的t替換為通常只有幾十到幾百微秒的采樣周期Ts，表達式變為反映kTs～（k＋1）Ts一個周期內的電流變化規律，同時實現了k時刻對k＋1時刻電流值的預測計算。然而，式（5）～式（7）包含較復雜的運算，不適合數字控制器的實現，故需進行簡化處理。

經離散周期Ts代換后，采用泰勒級數變化方法，將表達式展開成Ts的多項式形式，得到由k～k＋1時刻三個變化矢量和，并寫成矢量的相幅表達形式。前兩者為

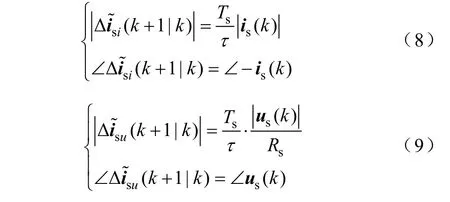
Δisω表達式較為復雜，矢量的近似處理受到電角速度ω 的影響，在低速的時候可以近似認為sinωt≈ωt、cosωt ≈1，然而速度較高時，特別是ωt接近1時，該近似不足以描述矢量。本文展開至Ts2，得到該矢量的相幅表達式為

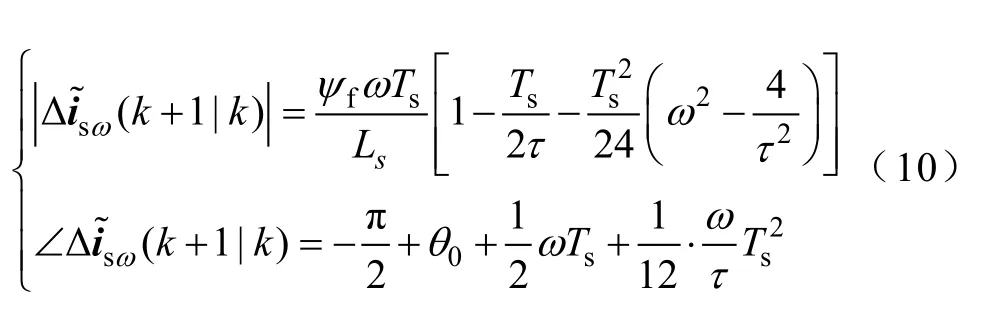
預測計算時，在誤差允許范圍內為減少計算量，式（10）可根據轉速大小，截取至Ts的0次、1次及2次項。

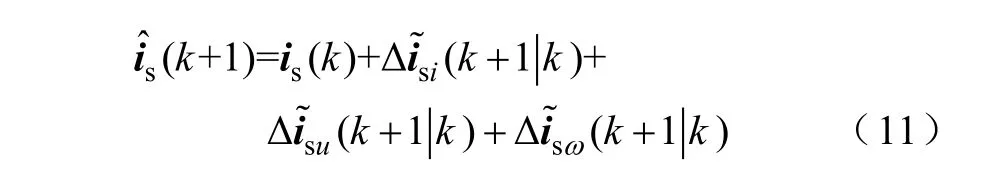
綜上，電流預測矢量表達式為電機電流預測規律的αβ 坐標矢量如圖2所示。

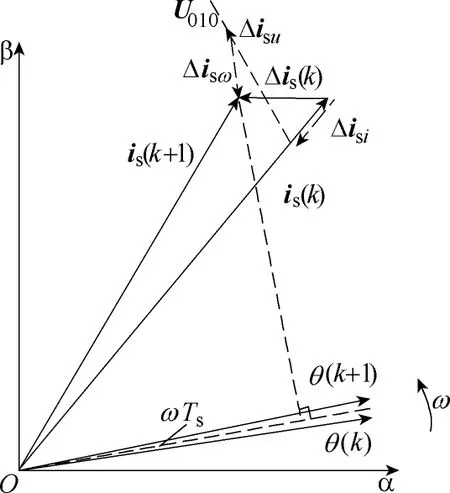
圖2　電流矢量動態預測Fig.2 Current vector dynamic prediction

2.2 電流矢量動態預測的誤差分析

電流矢量動態預測方法的計算過程經過了近似處理，其中存在矢量的計算誤差。定義矢量的距離d和相對距離dr為

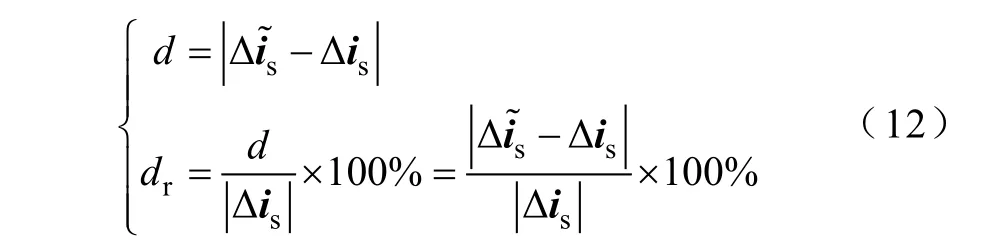
由此來作為計算誤差的評價標準。

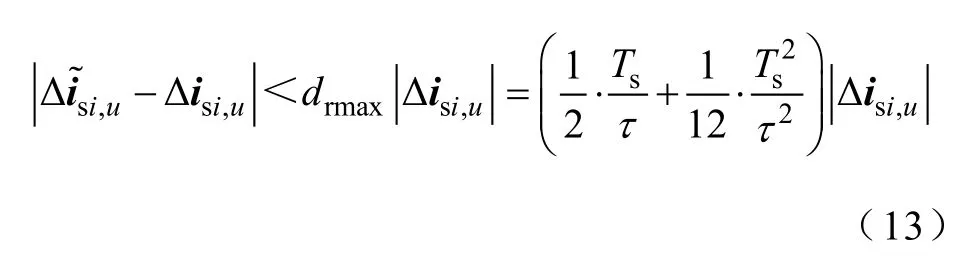
誤差只與電氣時間常數τ相關。針對不同的PMSM，Ts/τ值通常小于0.1，故可達到drmax＜5.1%，滿足工程中偏差在10%以內的要求。相對誤差的輪廓線如圖3所示。

根據Ts的取值范圍可以看出，圖4中給出的轉速范圍較寬，具有一定的普適性。而實際預測中，對于額定轉速10 000r/min以內的電機，截取至Ts的1次，該分量的預測誤差已經非常小：對于兩對極的電機，相對距離小于1%，四對極的將小于3%。

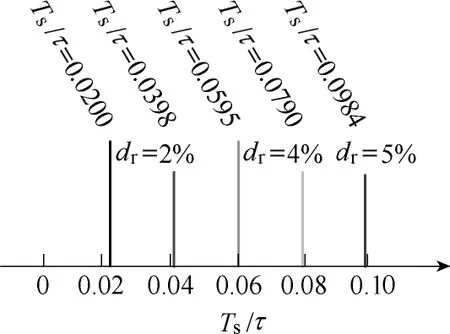
圖3　Ts/τ 引起的預測誤差輪廓曲線Fig.3 Error contour caused by Ts/τ

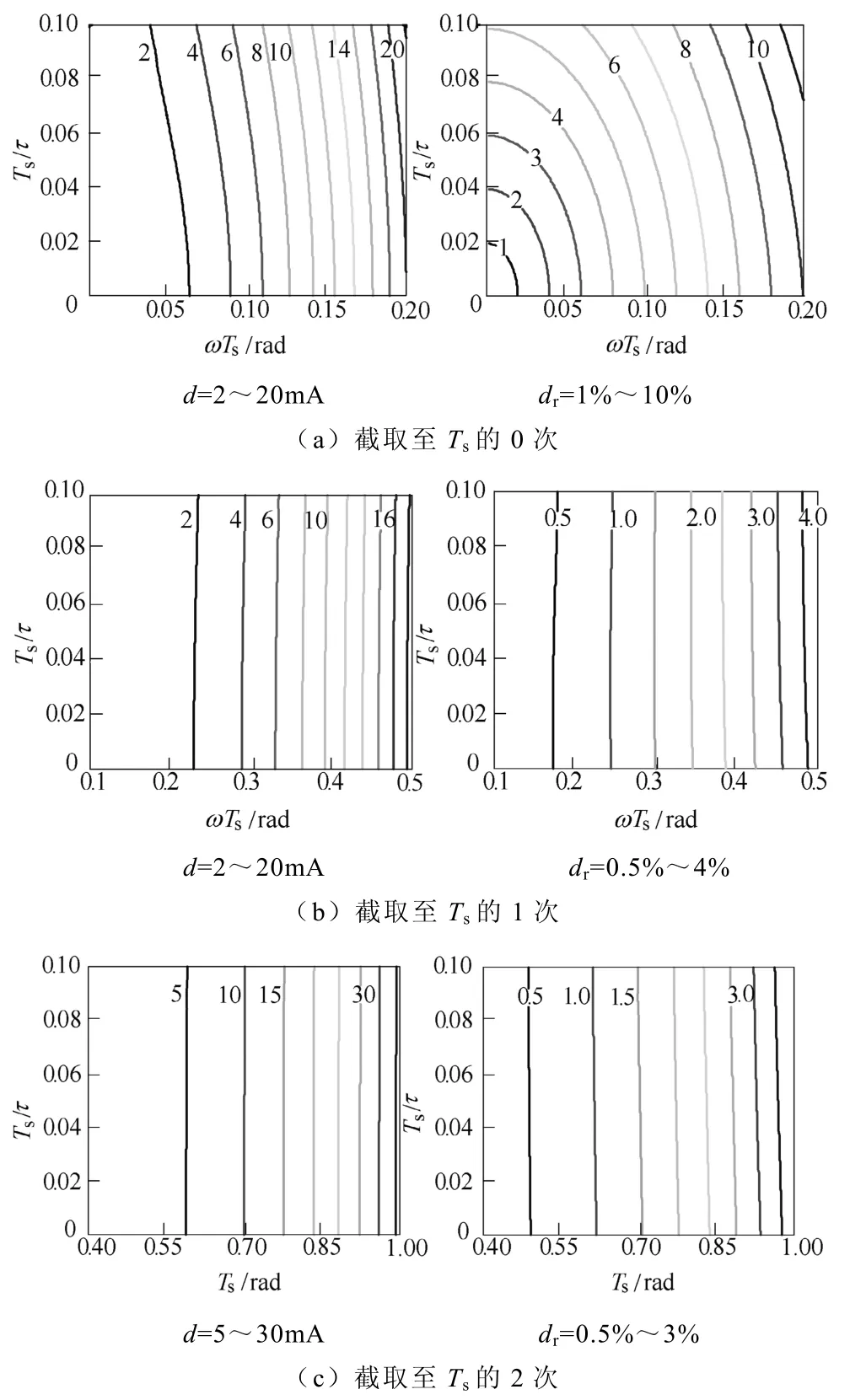
圖4　矢量距離d和相對距離dr的輪廓曲線Fig.4 Profile curves of vector distance and relative distance

此外，因電機參數引起的誤差，可利用在線辨識的方法進行參數修正。電機參數在線辨識的方法很多[12-14]，而電流預測的計算時間較短，在引入參數在線辨識時，不宜采用過于復雜的算法。文中可直接利用所提出的預測表達式，采用帶遺忘因子的遞推最小二乘法[15]辨識所需的Ls、Rs以及ψf等參數。

3 仿真及實驗

3.1 預測算法誤差的計算

以上從理論上分析了所提出的電流矢量預測方法的性能，以下針對某電機進行實驗驗證，實驗電機選用KOLLMONGEN公司M205B型電機，該電機參數見表1。

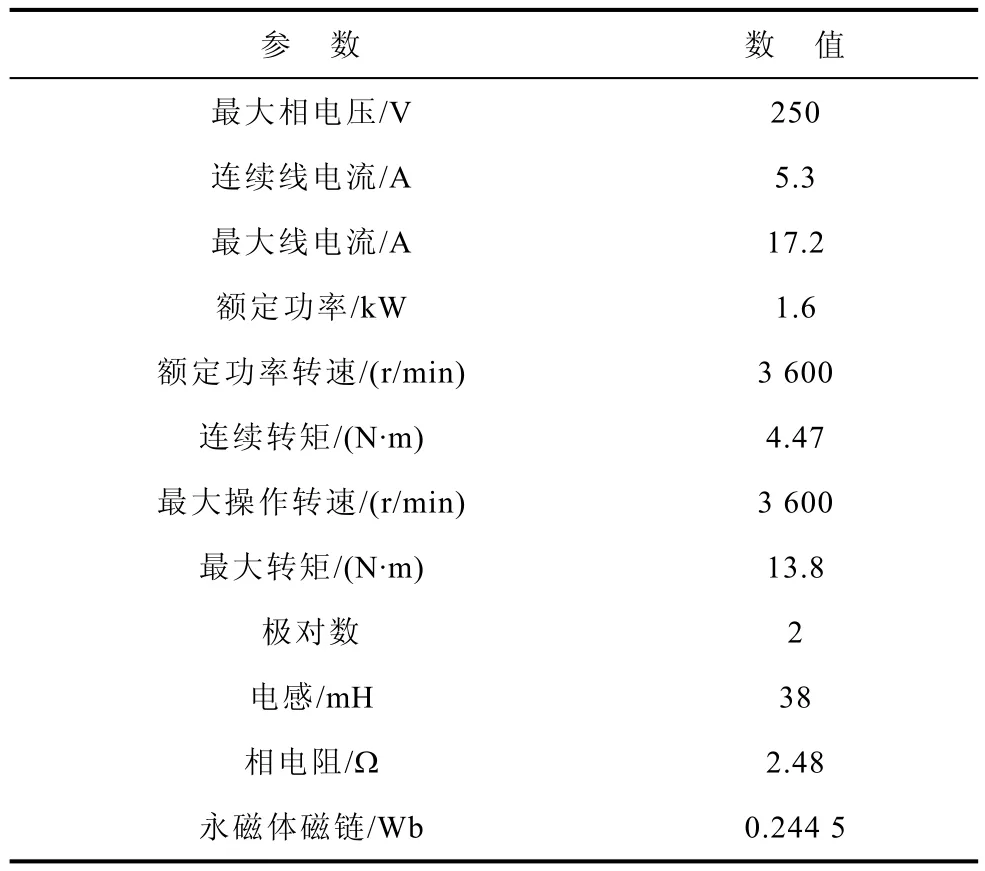
表1　電機參數Tab.1 Parameters of the PMSM

根據表1中參數可計算時間常數τ＝15.3ms。如果采樣周期Ts＝0.1ms，Ts/τ＝0.006 53，利用式（11）計算預測電流，其分解矢量Δisi、Δisu近似計算相對距離均為0.33%。而對于Δisω項，通過計算得到近似階次分別取0、1和2次時，不同轉速下Δisω電流矢量的誤差見表2（誤差保留四位小數）。

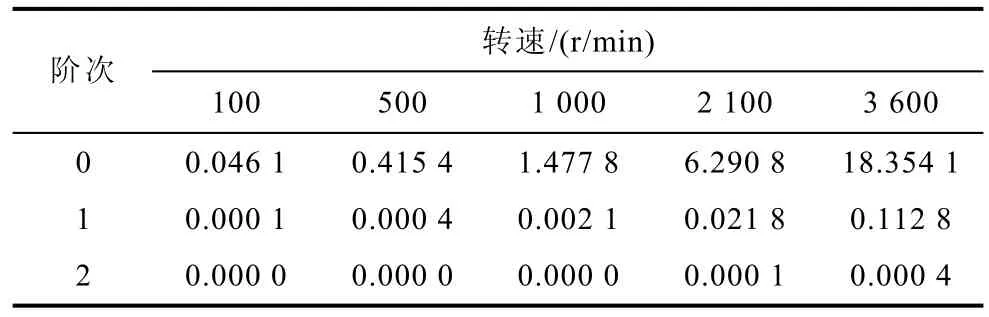
表2　電流矢量預測中Δisω項近似誤差Tab.2 Error of Δisωin the current vector prediction　（單位：mA）

由表2可以看出，誤差隨轉速的升高而增大，并且受近似程度的影響，階次越高，偏差越接近0。對于該電機，表2中最大的偏差為18.354 1mA，相對距離3.7%，相對電機電流預測值是誤差范圍內可以忽略的，但考慮預測準確度，本文在后續的實驗中，還將取到1階的計算準確度。

3.2 PMSM電流矢量預測仿真實驗

為檢驗本文預測算法的準確性，首先進行仿真實驗。仿真電機模型參數同表1，在文獻[16]離散電流控制方法的控制下，對電流矢量的動態變化進行預測。仿真條件為：直流母線電壓200V，開關頻率10kHz，同步采樣周期100μs，給定電流矢量幅值恒為5A。以下對電流矢量階躍變化以及連續運行情況進行仿真實驗。

當給定電流矢量從電角度30°階躍變化至60°，電流矢量的動態變化和預測結果如圖5a所示；A相電流波形及其預測波形如圖5b所示，圖中由于兩條曲線較為接近，故將預測電流波形向下平移1A的刻度以便于觀測。

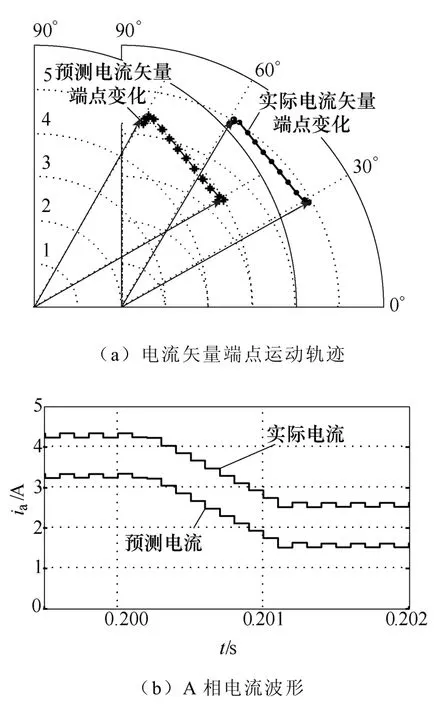
圖5　電流矢量階躍響應變化及預測結果Fig.5 Step response and predicting result of current vector

圖5a中指向30°和60°的矢量表示階躍變化前后的給定電流矢量，相應地，A相電流從4.33A變到2.5A。為清楚對比預測電流矢量端點軌跡及實際軌跡，將二者分別繪制在水平平移后的兩個極坐標中，從圖中可看出軌跡的一致性。圖5b中電流波形是模擬采樣過程經過0階保持器所輸出的電流波形，數值保持時間與采樣周期相同。利用式（12）計算電流矢量的距離，如圖6所示。從圖6中可以看出，電流矢量不變時，距離值在4mA上下，階躍變化處最大距離不超過11mA。

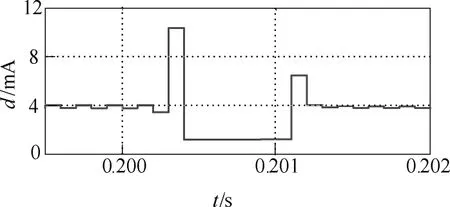
圖6　預測與實際的電流矢量距離dFig.6 Distance d of the current vector

采用恒頻控制方法控制電機連續運行，給定電流矢量按如圖7所示的12個空間離散位置以逆時針順序給定[17]。通過調節矢量的切換頻率，即可控制電機按不同速度運行，其切換頻率fconst與電機轉速n的關系為n＝2.5fconst，電流基波頻率fi＝fconst/12。

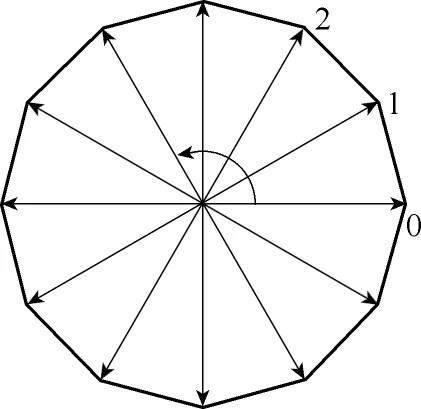
圖7　給定離散電流矢量Fig.7 The given discrete current vectors

當給定fconst＝400Hz時，電流基波頻率約為33.3Hz，電機恒定轉速為1 000r/min，其實際電流矢量端點的空間軌跡以及預測矢量軌跡如圖8a所示，A相電流波形如圖8b所示，其中預測電流波形向下平移約2A。

從圖8a中可看出預測的電流矢量端點軌跡與實際值基本一致，圖8b電流波形也說明預測結果的準確性。計算其預測電流矢量與實際矢量的距離d，得到對應時間段的預測偏差曲線，如圖9所示。距離d的數值大多小于11mA，電流矢量切換點處的距離最大不超過13mA，約為給定電流矢量幅值（5A）的0.26%，其預測偏差比較理想。

當給定fconst＝12Hz時，電流基波頻率為1Hz，此時電機轉速約30r/min。電流矢量端點的空間軌跡以及預測矢量軌跡如圖10a所示，其A相電流波形對比如圖10b所示，為清楚區分二者，將預測電流曲線向下平移2A。

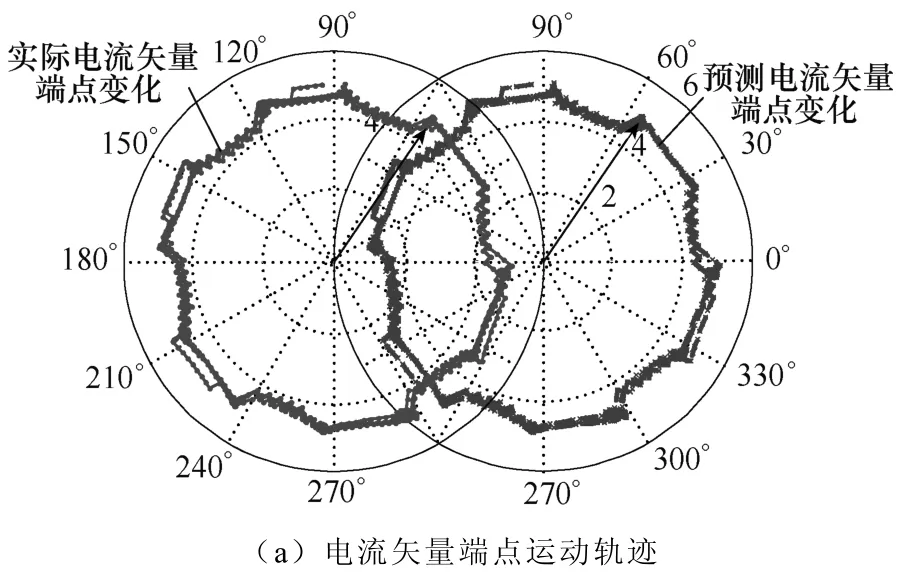
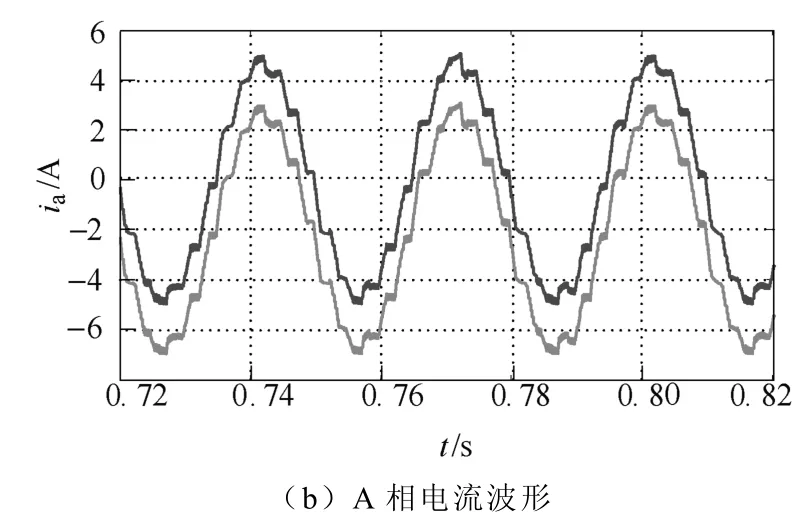
圖8　1 000r/min速度下的電流矢量及預測結果Fig.8 Current vector and predicting results at speed of 1 000r/min

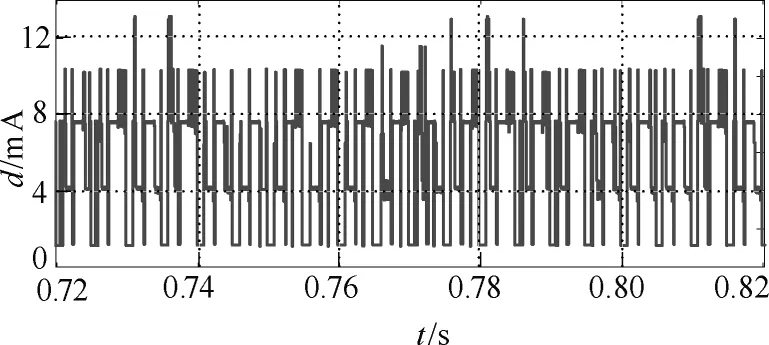
圖9　預測與實際的電流矢量距離dFig.9 Distance d of the current vector

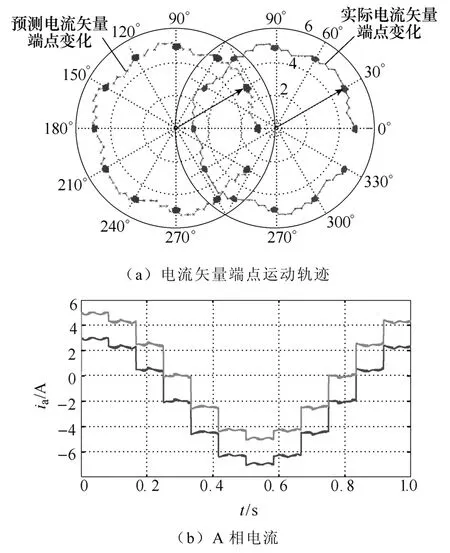
圖10　1Hz電流基波頻率下的電流矢量及預測結果Fig.10 Current vector and predicting result on frequency of 1Hz

圖10a中可以看出，電流矢量軌跡基本一致，在較低的電流頻率下，電流的動態預測效果仍然十分理想，從圖10b中亦可看出A相電流波形的一致性。通過計算矢量距離偏差d，得到圖11，其偏差最大值存在于電流矢量切換過程中，其值小于12mA，而在電流恒定的過程，預測矢量距離偏差在4mA上下浮動。

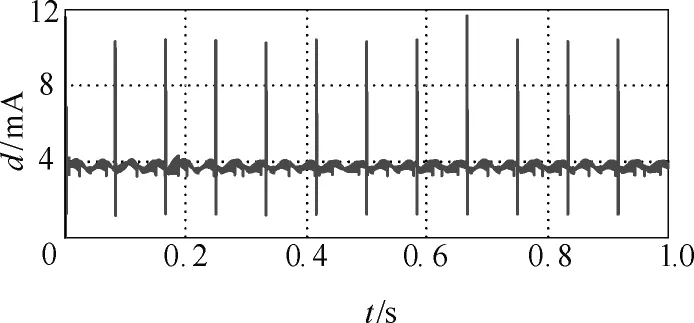
圖11　預測與實際的電流矢量距離dFig.11 Distance d of the current vector

從仿真實驗可以表明，本文所提出的電流預測方法有很好的效果，為電流預測控制提前計算控制量和減少控制延時提供了可靠的預測電流值。

3.3 PMSM電流矢量預測平臺實驗

實驗所用的PMSM參數同表1，實驗平臺基于TMS320F2407為核心的DSP控制器，并包含AD轉換和DA轉換等電路，功率部分采用智能功率模塊PM15RSH120對電機實施控制。預測計算在DSP中實現，經換算后由附帶的DA轉換模塊輸出預測結果和預測偏差至波形記錄儀。給定電流矢量幅值為5A，直流母線電壓200V，電機控制周期100μs，一個控制周期輸出一次。電流波形均為A相電流。預測偏差以矢量距離d計算。

圖12為電機以上述控制方法下的A相電流波形。由于預測電流與實測電流波形十分接近，為清楚對比，特別將預測電流向上平移三個小格。

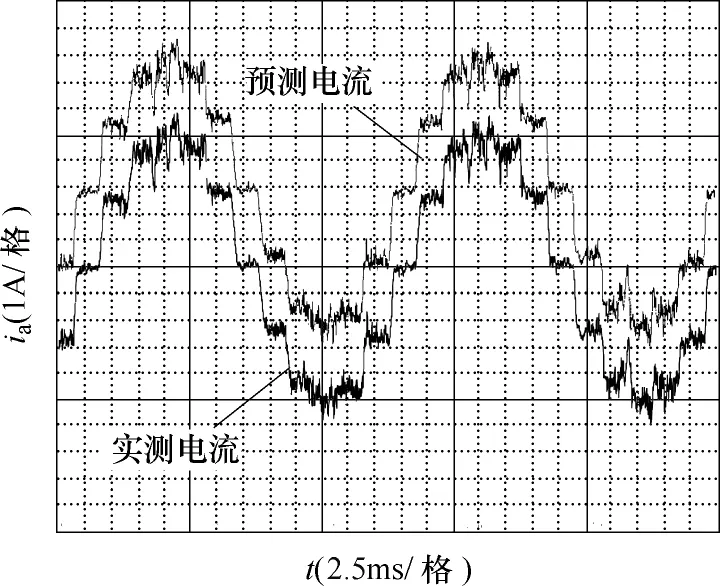
圖12　1 000r/min時的A相實測電流和電流預測波形Fig.12 Actual and predicting A-phase current waveform at speed of 1 000r/min

通過計算得到的輸出電流矢量距離d如圖13所示。通過數據計算的距離均值為120mA，為給定電流矢量幅值（5A）的2.4%。

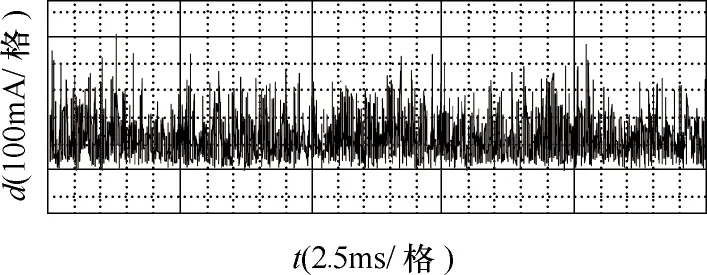
圖13　預測與實際的電流矢量距離dFig.13 Distance d of the current vectors

當電機按照電流基波頻率1Hz運行時，其A相電流波形如圖14所示，電機轉速30r/min，同樣將預測電流波形向上平移三個小格。

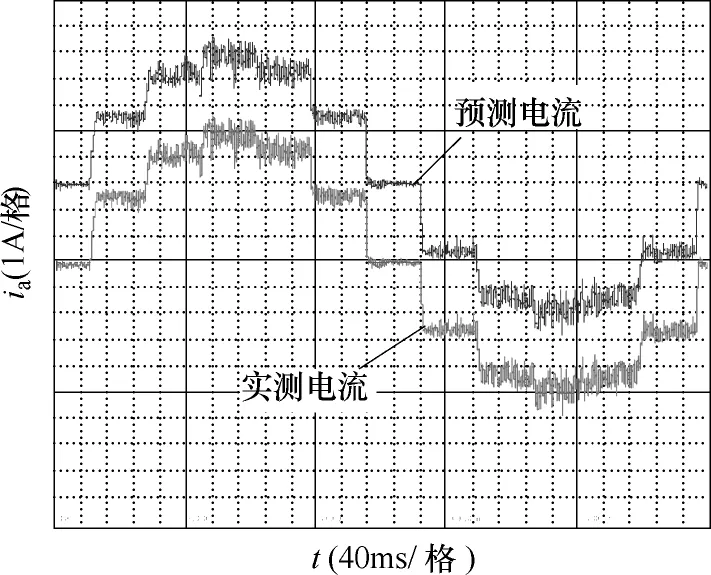
圖14　30r/min時的A相實測電流和電流預測波形Fig.14 Actual and predicting A-phase current waveform at speed of 30r/min

計算并用DA輸出電流矢量距離d如圖15所示，其距離均值為82.6mA，約為給定電流矢量幅值（5A）的1.65%。

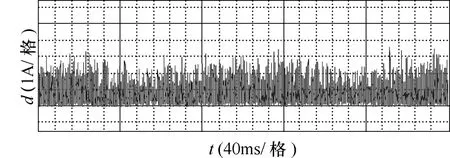
圖15　預測與實際的電流矢量距離dFig.15 Distance d of the current vectors

以上實驗可以說明本文所提出的算法在實際電機控制應用中同樣具有良好的效果。

4 結論

高性能的PMSM電機控制系統對電流環要求較高，本文提出的以電流矢量為目標的電流預測方法可以準確地預測電流矢量的變化趨勢。通過分析PMSM電流的動態響應，將電流矢量在離散周期上的變化量分解為三個獨立的分量，并利用泰勒級數得到易于實現的近似表達式，從而實現了電流矢量的動態預測。同時，誤差分析給出了算法的準確性，尤其是對反電動勢引起的電流矢量變化，給出了不同速度下不同階次的通用表達式，并得出誤差的輪廓線圖，為匹配相應轉速下預測計算的參數選擇提供了理論依據，并由仿真進行了驗證。最后通過實驗得出不同轉速下的預測偏差，實驗結果證明了本文提出的電流矢量預測算法具有良好的性能，對提高電流控制的準確度和跟隨速度有十分重要的意義。

參考文獻

[1]Moon H T,Youn M J.Predictive current control for PMSM with consideration of calculation delay[J].Electronics Letters,2001,37（24）:1488-1489.

[2]Abu-Rub H,Guzinski J,Krzeminski Z,et al.Predictive current control of voltage source inverters[J].IEEE Transactions on Industrial Electronics Society,2004,51（3）:585-593.

[3]陳書錦,李華德,李擎,等.永磁同步電動機起動過程控制[J].電工技術學報,2008,23（7）:39-44.Chen Shujin,Li Huade,Li Qing,et al.Start process control of permanent magnet synchronous motors[J].Transactions of China Electrotechnical Society,2008,23（7）:39-44.

[4]Weigold J,Braun M.Predictive current control using identification of current ripple[J].IEEE Transactions on Industrial Electronics,2008,55（12）:4346-4353.

[5]Sakata K,Fujimoto H,Peretti L,et al.Enhanced speed and current control of PMSM drives by perfect tracking algorithms[C]//The International Power Electronics Conference,2010:587-592.

[6]牛里,楊明,劉可述,等.永磁同步電機電流預測控制算法[J].中國電機工程學報,2012,32（6）:131-137.Niu Li,Yang Ming,Liu Keshu,et al.A predictive current control scheme for permanent magnet synchronous motors[J].Proceedings of the CSEE,2012,32（6）:131-137.

[7]牛里,楊明,王庚,等.基于無差拍控制的永磁同步電機魯棒電流控制算法研究[J].中國電機工程學報,2013,33（15）:78-85.Niu Li,Yang Ming,Wang Geng,et al.Research on the robust current control algorithm of permanent magnet synchronous motor based on deadbeat control principle [J].Proceedings of the CSEE,2013,33（15）:78-85.

[8]楊南方,駱光照,劉衛國.誤差補償的永磁同步電機電流環解耦控制[J].電機與控制學報,2011,15（10）:50-54,62.Yang Nafang,Luo Guangzhao,Liu Weiguo.Decoupling control of current loop for permanent magnet synchronous motor drives using error compensation[J].Electric Machines and Control,2011,15（10）:50-54,62.

[9]萬山明,吳芳,黃聲華.永磁同步電機的數字化電流控制環分析[J].華中科技大學學報:自然科學版,2007,35（5）:48-51.Wan Shanming,Wu Fang,Huang Shenghua.Analysis of digital current control loop for a PMSM[J].Journal of Huazhong University of Science and Technology（Nature Science Edition）,2007,35（5）:48-51.

[10]Ambrozic V,Fiser R,Nedeljkovic D.Direct current control-a new current regulation principle,IEEE Transactions on Power Electronics,2003,18（1）:495-503.

[11]王偉華,肖曦,丁有爽.永磁同步電機改進電流預測控制[J].電工技術學報,2013,28（3）:50-55.Wang Weihua,Xiao Xi,Ding Youshuang.An improved predictive current control method for permanent magnet synchronous motors[J].Transactions of China Electrotechnical Society,2013,28（3）:50-55.

[12]徐東,王田苗,劉敬猛,等.基于參數辨識的永磁同步電機電流精確控制方法[J].電力自動化設備,2008,28（11）:30-35.Xu Dong,Wang Tianmiao,Liu Jingmeng,et al.Precise current control of PMSM based on parameter identification[J].Electric Power Automation Equipment,2008,28（11）:30-35.

[13]王松,劉明光,石雙雙,等.基于卡爾曼濾波和神經網絡的PMSM參數辨識[J].北京交通大學學報,2010,34（2）:124-127,136.Wang Song,Liu Mingguang,Shi Shuangshuang,et al.Identification of PMSM based on EKF and Kalman neural network[J].Journal of Beijing Jiaotong University,2010,34（2）:124-127,136.

[14]劉朝華,李小花,周少武,等.面向永磁同步電機參數辨識的免疫完全學習型粒子群算法[J].電工技術學報,2014,29（5）:118-126.Liu Zhaohua,Li Xiaohua,Zhou Shaowu,et al.Comprehensive learning particle swarm optimization algorithm based on immune mechanism for permanent magnet synchronous motor parameter identification[J].Transactions of China Electrotechnical Society,2014,29（5）:118-126.

[15]楊立永,張云龍,陳智剛,等.基于參數辨識的PMSM電流環在線自適應控制方法[J].電工技術學報,2012,27（3）:86-91.Yang Liyong,Zhang Yunlong,Chen Zhigang,et al.On-line adaptive control of PMSM current-loop based on parameter identification[J].Transactions of China Electrotechnical Society,2012,27（3）:86-91.

[16]Dong Yan,Jing Kai,Sun Hexu,et al.Discrete current control strategy of permanent magnet synchronous motors[J].Journal of Applied Mathematics,2013（22）:1-9.

[17]董硯,孫鶴旭,包致遠,等.基于矩角控制的永磁同步電動機位置控制系統[J].電工技術學報,2006,21（1）:86-91.Dong Yan,Sun Hexu,Bao Zhiyuan,et al.Permanent magnet synchronous motor position control system based on torque-angle control[J].Transactions of China Electrotechnical Society,2006,21（1）:86-91.

荊 鍇 男，1987年生，博士研究生，研究方向為電機系統及其控制。

E-mail:jingkai_1082@126.com

孫鶴旭 男，1956年生，教授，博士生導師，研究方向為工程系統與控制。

E-mail:hxsun@hebut.edu.cn（通信作者）

Stator Current Dynamic Prediction of Permanent Magnet Synchronous Motor Targeting the Current Vector

Jing Kai1Sun Hexu1,2Dong Yan1Zheng Yi1
（1.School of Control Science and Engineering Hebei University of Technology Tianjin 300130 China 2.Hebei University of Science and Technology Shijiazhuang 050018 China）

AbstractThis paper proposed a dynamic prediction method for stator current of permanent magnet synchronous motor（PMSM）,targeting the current vector.The dynamic response of the current vector has been studied on the αβ stationary frame,and the vector is decomposed into three components caused by different actions.Each component is truncated and approximated by Taylor series,and the proposed method is thereafter obtained.In addition,through the error analysis of each component,a basis of parameter selection and application is provided.Experiments verify the accuracy of the prediction method.

Keywords：Permanent magnet synchronous motor,current vector,current prediction,error analysis

作者簡介

收稿日期2014-03-21 改稿日期 2014-06-24

中圖分類號：TM341