順瓜摸藤溯流徂源
——名師羅鳴亮構(gòu)建“講道理”數(shù)學(xué)課堂教學(xué)策略解讀

陳華強(qiáng)

逆向思維是創(chuàng)造性思維的重要形式，是指由果索因、知本求源，從原問題的相反方向著手的一種思維過程。這種思考方法富有跳躍性和挑戰(zhàn)性。

想起兒時一個真實(shí)的生活場景：母親讓我們到南瓜地里數(shù)每條藤上的瓜數(shù)，每條藤上結(jié)的瓜果最好不多于四個，多了會影響瓜果的質(zhì)量。瓜地的藤條錯綜復(fù)雜，枝莖纏結(jié)，有時很難從粗莖上找瓜，母親教我們“順著瓜摸藤”——找到一個瓜，順著這個瓜摸到它的藤，就能知道這條藤上的瓜果數(shù)，此法果然見效。溯流徂源，是指順支流上溯河源，與“順瓜摸藤”異曲同工。

觀名師羅鳴亮的諸多經(jīng)典課例，我們發(fā)現(xiàn)：他通過“順瓜摸藤”與“溯流徂源”，引發(fā)學(xué)生的逆向思維，讓學(xué)生在正反思維的碰撞和融通中理解數(shù)學(xué)知識的內(nèi)涵，進(jìn)而構(gòu)建起“講道理”的數(shù)學(xué)課堂。

一、活用教具，引逆向思維

逆向思維能力的培養(yǎng)，有助于學(xué)生打破思維的定勢，促使學(xué)生全面、靈活地考慮問題，探尋不同的思路，提出獨(dú)到的見解，在思考的過程中達(dá)到求同存異，這樣會使學(xué)生在學(xué)習(xí)中獲得更大的收獲，學(xué)生的思維也會拓展出另一片“空間”。因此，教師在教學(xué)中應(yīng)該有意識地加強(qiáng)反向思維的訓(xùn)練，靈活變通地利用教學(xué)具、教學(xué)例題，引導(dǎo)學(xué)生反向思維，造就課堂精彩。

1.大信封，多用途。

以《平行四邊形和梯形》一課教學(xué)為例，一個簡單的道具——“信封”，引出了一場課堂的大討論。

【教學(xué)片斷一】

出示問題情境：黑板上貼一個信封，外面寫著“四邊形”，從信封口露出一個四邊形的一部分（如圖所示）。猜想：這四邊形可能是什么？

對于學(xué)生的多種猜測，教師不置可否，緊接著出示8個四邊形，讓學(xué)生分一分，在學(xué)生領(lǐng)會了梯形和平行四邊形不同之后，羅老師繼續(xù)在“猜”上面做足了文章。

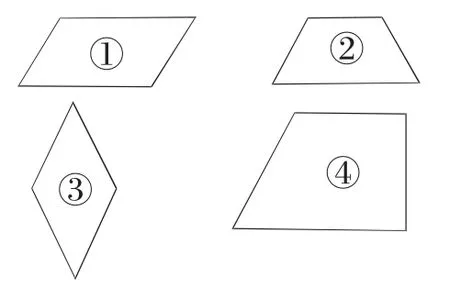
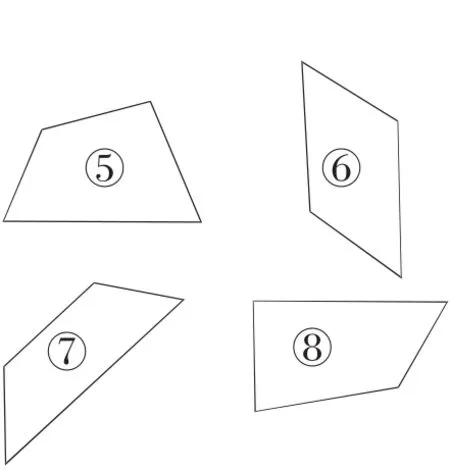
設(shè)問：信封里可以是不規(guī)則圖形嗎？為什么？

教師抽出信封的圖形，是一個跟“平行四邊形”長得非常像的“梯形”。

出示圖片后追問：為什么它不是平行四邊形？你怎么知道？

本環(huán)節(jié)，羅老師不是直接呈現(xiàn)各種多邊形讓學(xué)生判斷，而是通過“信封”讓學(xué)生先猜，再像這樣從反向的角度提問，引發(fā)了學(xué)生對知識的辯駁，更好地理解了平行四邊形和梯形的特性。

2.小卡片，大學(xué)問。

幾張小卡片，在羅老師的課堂上也能碰撞出精彩的思維火花，趣味無窮。他引導(dǎo)學(xué)生反向思考問題，幫助學(xué)生變通思考方法和策略，其中大有學(xué)問。

【教學(xué)片斷二】（出自《近似數(shù)》一課）

1.（黑板貼出6張空白卡片）：杭州動物園占地面積是幾位數(shù)？

2.（翻開最高位兩張卡片，分別是 2、3）設(shè)想：如果后面的四位都是0，那就是幾萬？

3.追問：它不是整萬數(shù)，你覺得它會接近二十幾萬呢？（分別翻開最后面的兩張卡片）可以了嗎？為什么還是無法確定？

4.討論：為什么一定要看千位？為什么一定是 5、6、7、8、9呢？如果是比5小的數(shù)呢？

正所謂“大道至簡”，觀羅老師的許多精彩課例，用簡單的教具演繹著簡約的教學(xué)，復(fù)雜的問題凝聚著簡要的道理。信封、卡片是他慣用的“兵器”“制勝法寶”，既懸疑又變通，聚集著許多思維的亮點(diǎn)，同時也引得學(xué)生不僅對數(shù)學(xué)知識本身從順逆兩側(cè)獲得全面深刻的理解，而且在潛移默化中獲得思維深度和廣度的提升。

二、追思溯想，導(dǎo)逆向思維

畢達(dá)哥拉斯說過：“數(shù)學(xué)重要的不是知道了什么，而是怎么知道什么。”數(shù)學(xué)講究理性，理通則意達(dá)。“為什么”常成為許多數(shù)學(xué)教師的口頭禪，這三個字促使學(xué)生積極轉(zhuǎn)動思維，與別人交流想法。一個優(yōu)秀的數(shù)學(xué)教師往往是一個愛問問題的教師，是一個講道理的教師。正所謂“以理服人”，課堂上讓學(xué)生交流心得、講通道理，就是讓學(xué)生的思維得以提升的最好途徑。

【教學(xué)片斷三】（出自《三角形的分類》一課）

1.（趣味游戲）創(chuàng)設(shè)問題情境：C點(diǎn)跑到了方格圖外，現(xiàn)在如果連接這三點(diǎn)會是什么三角形？

2.設(shè)想：C點(diǎn)在往下移動，當(dāng)C點(diǎn)移動到你覺得和A點(diǎn)、B點(diǎn)能連成一個直角三角形的時候，你就大膽地站起來喊“停”！

（C點(diǎn)回到了格子圖內(nèi)，讓學(xué)生細(xì)致觀察三點(diǎn)從銳角三角形慢慢變到直角三角形再到鈍角三角形的變化。）

3.思考：給你三個點(diǎn)，你就能連接成一個三角形嗎？

4.點(diǎn)睛：不行，若三點(diǎn)成一條直線呢？記住：“少一些想當(dāng)然，多一些理性的思考。”

本環(huán)節(jié)的設(shè)計，可謂匠心獨(dú)具！羅老師不是直接讓學(xué)生判斷三角形，而是根據(jù)移動的C點(diǎn)，反向思考可能會拼成什么三角形。“少一些想當(dāng)然，多一些理性思考。”教師予以追問質(zhì)疑，讓學(xué)生講道理、說緣由，思維得到了提升。最后的點(diǎn)睛之筆，又一次叩響了學(xué)生的心靈。

三、由果析因，煉逆向思維

逆向思維是一種從反面觀察事物，變換角度處理問題，由果析因的思維方式。教學(xué)的本質(zhì)是思維對話。因而，逆向思維是教學(xué)中不可或缺的部分，在理解問題時不僅取順向，也要取逆向；不僅從因到果，也要由果析因，使問題得到解決，提高分析問題的能力，鍛煉逆向思維。觀羅鳴亮老師兩次執(zhí)教的《長方形的面積》稍有不同，但在設(shè)計上都承襲同一思路：知識不是教出來的，是學(xué)生自己感悟出來的。學(xué)生的感悟和思維是多向的，既有利用綜合法對問題進(jìn)行建構(gòu)，也有用分析法進(jìn)行判斷。而這種從結(jié)果出發(fā)，思考問題的分析法就是一種反向思維的方法，在這節(jié)課上一覽無遺。

【教學(xué)片斷四】（出自《長方形的面積》一課）

1.出示問題情境：一個圖形的面積是3平方分米，它是什么樣的？你是怎么想的？

2.反議：給格子圖中長和寬是15、10的長方形涂色，有的同學(xué)速度很快，想一想他們?yōu)槭裁催@么快？

3.設(shè)問：信封里的這個長方形,要求它的面積怎么辦？這個長方形的面積也是20平方厘米，它的長和寬可能是多少厘米？怎么想的？

4.討論：我家的長方形很苗條，你覺得是哪個？我家的長方形的長有可能比20厘米還長嗎？

5.思辨：有一個長方形，每行有4個，有2行？面積是多少？

本環(huán)節(jié)，羅老師在問題的提問方式上、觸發(fā)學(xué)生思考的思維點(diǎn)上都做足了文章。隨著一個個問題的出現(xiàn)，引發(fā)了學(xué)生的思維沖突，培養(yǎng)了反向思維的能力。在學(xué)生發(fā)現(xiàn)新知識的過程中，打破順向思維的定勢，從不同的角度分析問題，探求多種不同的思路，運(yùn)用不同的解題方法求異求新，既培養(yǎng)了學(xué)生的發(fā)散思維，又提高了學(xué)生逆向思維的能力。