探究一次函數(shù)模型的應(yīng)用
陳曉燕
[摘 要] “來源于生活,應(yīng)用于生活”是數(shù)學(xué)本質(zhì)所在. 將生活中的問題抽象為數(shù)學(xué)模型,進(jìn)而利用數(shù)學(xué)模型來解決問題是數(shù)學(xué)應(yīng)用于生活的重要體現(xiàn). 本文抽象出地鐵票價(jià)、乘客量與盈利之間的關(guān)系,通過變式引導(dǎo)學(xué)生對(duì)數(shù)學(xué)模型的應(yīng)用展開探究,使得數(shù)學(xué)知識(shí)在生活中有了用武之地.
[關(guān)鍵詞] 一次函數(shù);模型應(yīng)用;地鐵票價(jià);盈利;虧損
在學(xué)習(xí)某一數(shù)學(xué)知識(shí)的過程中,學(xué)生經(jīng)常會(huì)提出這樣的問題:老師,學(xué)了這個(gè)知識(shí)有什么用?如果我們回答:為了解題,為了考試. 顯然沒有說服力. 就目前我們所學(xué)的知識(shí),難道真的找不到它的用武之地嗎?本文以筆者所上的一節(jié)“一次函數(shù)模型應(yīng)用”課為例來說明函數(shù)的應(yīng)用.
在本次課之前,筆者所教授的班級(jí)已經(jīng)學(xué)習(xí)了正比例函數(shù)與一次函數(shù),教學(xué)片段展示如下.
問題1:你能用我們學(xué)過的函數(shù)模型近似地描述“某地鐵線路的盈利額與乘客量之間的關(guān)系”嗎?
生:首先應(yīng)確定票價(jià),設(shè)票價(jià)為a,設(shè)盈利額為y,乘客量為x,則可用正比例函數(shù)模型,即y=ax來描述.
師:大家同意該生的觀點(diǎn)嗎?
生:結(jié)合實(shí)際情況來看,地鐵運(yùn)營要有固定的成本,所以當(dāng)乘客數(shù)x=0時(shí),利潤y應(yīng)為負(fù)值,所以它應(yīng)該是一次函數(shù)模型,即y=ax+b.
師:好,我們來回顧一下一次函數(shù)的相關(guān)知識(shí).
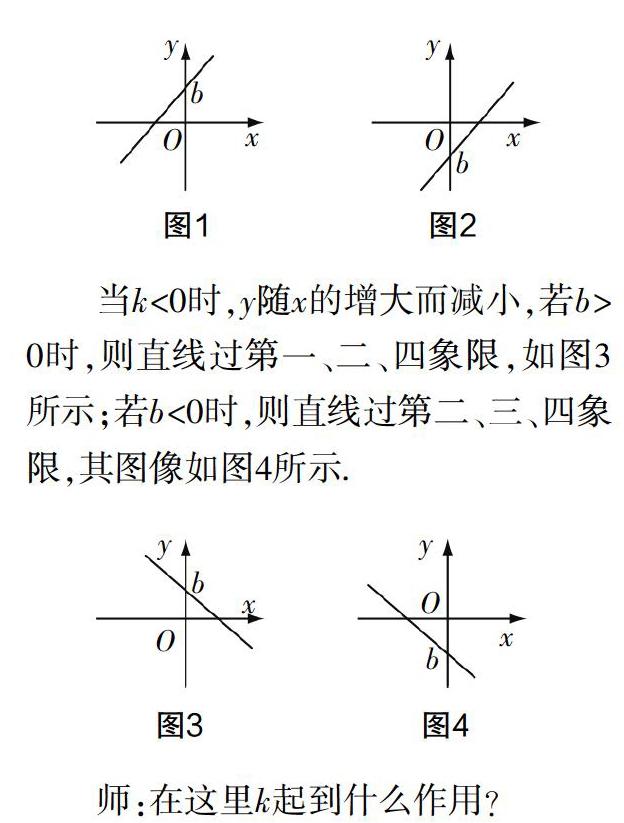
生:一次函數(shù)的關(guān)系式是y=kx+b,其圖像是一條直線. 當(dāng)k>0時(shí),y隨x的增大而增大. 若b>0時(shí),則直線過第一、二、三象限,如圖1所示;若b<0時(shí),則直線過第一、三、四象限,其圖像如圖2所示.
當(dāng)k<0時(shí),y隨x的增大而減小,若b>0時(shí),則直線過第一、二、四象限,如圖3所示;若b<0時(shí),則直線過第二、三、四象限,其圖像如圖4所示.
師:在這里k起到什么作用?
生:反映了直線的傾斜程度,當(dāng)k>0時(shí),k越大,直線越陡峭;k越接近于0,直線越平緩. 當(dāng)k<0時(shí),k越小,直線越陡峭;k越接近于0,直線越平緩.
師: 那么這個(gè)函數(shù)的圖像大致形狀是什么樣的?
生:如圖2所示.
師:同學(xué)們是否有異議?
生:函數(shù)是有定義域限制的,乘客量應(yīng)是正整數(shù),而且是有限的,所以該函數(shù)的圖像應(yīng)為在某條線段上的一些整點(diǎn).
師:非常好!為了研究方便,我們就近似地用直線來表示這個(gè)函數(shù)的圖像.
評(píng)析:通過問題的引入,引導(dǎo)學(xué)生聯(lián)系所學(xué)知識(shí)與生活問題建立關(guān)聯(lián). 但要注意生活問題因有其實(shí)際意義,故不能直接套用所學(xué)數(shù)學(xué)模型,應(yīng)根據(jù)實(shí)際問題對(duì)函數(shù)模型進(jìn)行相應(yīng)的調(diào)整. 將生活中的數(shù)學(xué)問題構(gòu)造出的模型,大多為一種符號(hào)模型,即把題目中的已知量、未知量、常量、變量分別列出,再添加題目的各種約束條件,進(jìn)而得出相應(yīng)的數(shù)學(xué)結(jié)論.
問題2:如果目前這條線路處于虧損狀態(tài),你們有什么辦法令其扭虧為盈嗎?
生:提高票價(jià).
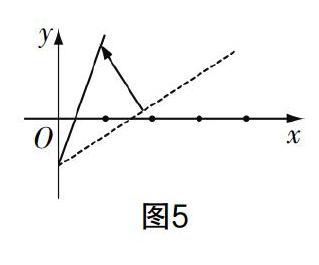
師:雖然簡(jiǎn)單粗暴,但確實(shí)是行之有效的辦法. 如果提高了票價(jià),那么函數(shù)的圖像有什么變化?
生:提高票價(jià),即直線的傾斜程度變得更陡峭,如圖5所示.
師:當(dāng)然,票價(jià)提高多少,還需要做科學(xué)的調(diào)查,我們?cè)诖讼炔蛔錾钊胙芯? 還有沒有其他的辦法?
生:降低成本.
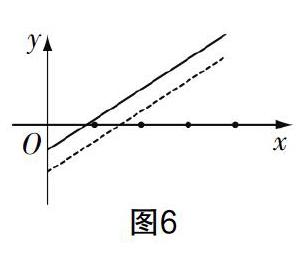
師:你很有奉獻(xiàn)精神. 如果降低了成本,函數(shù)的圖像又會(huì)有什么變化?
生:票價(jià)不變,說明直線的傾斜程度不變,直線向上平移,如圖6所示.
師:當(dāng)然實(shí)際情況可能不像我們所想象的那樣簡(jiǎn)單,地鐵公司可能有更科學(xué)的定價(jià)方案.
評(píng)析:通過對(duì)問題1進(jìn)行變式,由函數(shù)模型與實(shí)際問題的關(guān)系,利用函數(shù)模型實(shí)現(xiàn)對(duì)實(shí)際問題的處理,從而提出有針對(duì)性的策略.
問題3:請(qǐng)同學(xué)們思考一下,如果我們也近似用一次函數(shù)模型來表示,那么隨著票價(jià)的增加,乘客量會(huì)有什么變化?
生:票價(jià)越高,乘坐地鐵的人就會(huì)越少. 設(shè)票價(jià)為x,乘客量為y,則y=kx+b(k<0).
師:若票價(jià)與乘客量之間的關(guān)系如圖7所示,則票價(jià)為多少時(shí),盈利額最大?
生:由圖知,當(dāng)票價(jià)x=1時(shí),y=10;x=5時(shí),y=2.將其代入直線方程y=kx+b,得k+b=10,5k+b=2, 解得k=-2,b=12.所以函數(shù)關(guān)系式為y=-2x+12.
師:能否求出盈利額的最大值?以及當(dāng)盈利額最大時(shí),票價(jià)應(yīng)定為多少?
生:設(shè)盈利額為L,成本為B,則有L=x(-2x+12)-B. 因此當(dāng)票價(jià)x=3時(shí),盈利額最大,最大值為18-B.
師:函數(shù)模型確定以后,我們就可以用于決策方案的確定. 當(dāng)然具體問題的處理不像我們所設(shè)想的這樣簡(jiǎn)單.
評(píng)析:把生活問題轉(zhuǎn)化為相應(yīng)的數(shù)學(xué)模型后,再根據(jù)要求對(duì)該模型進(jìn)行求解.通常情況下,把實(shí)際應(yīng)用問題數(shù)學(xué)化之后,生活問題便成為普通的數(shù)學(xué)問題了.
問題4:該地鐵公司決定實(shí)行按照乘車?yán)锍谭侄斡?jì)價(jià). 方案如下:
乘坐地鐵方案6公里(含)內(nèi)3元;
6公里至12公里(含)4元;
12公里至22公里(含)5元;
22公里至32公里(含)6元;
32公里以上部分,每增加1元可乘坐20公里(含).
已知在某段線路上,任意一站到A站的票價(jià)不超過5元,現(xiàn)從那些只乘坐該線路地鐵,且在A站出站的乘客中隨機(jī)選出120人,他們乘坐地鐵的票價(jià)統(tǒng)計(jì)如圖8所示. 如果從那些只乘坐該線路地鐵,且在A站出站的乘客中任選1人,試估計(jì)此人乘坐地鐵的票價(jià)小于5元的概率.
生:記事件A為“此人乘坐地鐵的票價(jià)小于5元”. 由統(tǒng)計(jì)圖可知,得120人中票價(jià)為3元、4元、5元的人數(shù)分別為60,40,20.
所以票價(jià)小于5元的有60+40=100(人).
故120人中票價(jià)小于5元的頻率是=.?搖?搖?搖?搖?搖?搖?搖?搖
所以估計(jì)此人乘坐地鐵的票價(jià)小于5元的概率P(A)=.
師:使用市政交通一卡通刷卡,每自然月內(nèi)每張卡支出累計(jì)滿100元以后的乘次,價(jià)格給予8折優(yōu)惠;滿150元以后的乘次,價(jià)格給予5折優(yōu)惠;支出累計(jì)達(dá)到400元以后的乘次,不再享受打折優(yōu)惠.
某同學(xué)上學(xué),需要乘坐地鐵15.9公里到達(dá)學(xué)校,每天上下學(xué)共乘坐兩次,每月按上學(xué)22天計(jì)算. 如果該同學(xué)每次乘坐地鐵都使用市政交通一卡通,那么他每月第21次乘坐地鐵里時(shí),他刷卡支出的費(fèi)用是________元;他每月上下學(xué)乘坐地鐵的總費(fèi)用是_______元.
生:該生每天的上下學(xué)的費(fèi)用分別為5元,即每天10元. 10天后花費(fèi)100元,第21次乘坐地鐵時(shí),價(jià)格給予8折優(yōu)惠,此時(shí)花費(fèi)5×0.8=4元.
10天后的費(fèi)用為100元,再過6天后花費(fèi)8×6=48元,此時(shí)合計(jì)花費(fèi)148元.
第17天上午累積花費(fèi)148+4=152元,從第17天的下午開始車費(fèi)為5×0.5=2.5元. 此時(shí)到22天結(jié)束還需要要乘車11次,需要花費(fèi)2.5×11=27.5元.
故合計(jì)152+27.5=179.5元.
答案為4;179.
評(píng)析:通過仔細(xì)審視題目信息,弄清題目中的每一個(gè)詞語的含義,深入挖掘其中所涉及的隱含信息;再將題目中生活、生產(chǎn)中的語言準(zhǔn)確地用我們所學(xué)數(shù)學(xué)語言表達(dá)出來,分清條件和結(jié)論,理順題目中各種數(shù)量之間的關(guān)系,聯(lián)想歸結(jié)為自己所熟悉的某種基本數(shù)學(xué)關(guān)系.
總之,應(yīng)用函數(shù)模型解決實(shí)際問題時(shí)可遵從如下步驟:首先,對(duì)實(shí)際問題進(jìn)行模型概括:探究實(shí)際生活問題中各變量間的關(guān)系,并用x,y分別表示問題中的變量;其次,確立函數(shù)模型:將變量y表示為x的函數(shù),建立的函數(shù)模型即為函數(shù)的解析式;最后,求解函數(shù)模型:根據(jù)實(shí)際生活問題所需要解決的目標(biāo)及函數(shù)式的結(jié)構(gòu)特點(diǎn),準(zhǔn)確選擇相應(yīng)的函數(shù)知識(shí)求模型的解,并將所得結(jié)論應(yīng)用到實(shí)際問題中.
當(dāng)然,數(shù)學(xué)模型的應(yīng)用不僅局限于此. 數(shù)學(xué)來源于生活,應(yīng)用于生活,我們要善于觀察身邊的事物,用所學(xué)的知識(shí)去解決生活中的問題,讓數(shù)學(xué)變得不再枯燥. 筆者在此拋磚引玉,希望對(duì)讀者有所啟發(fā),共同探究應(yīng)用數(shù)學(xué)知識(shí)解決生活問題,真正實(shí)現(xiàn)學(xué)有所用、學(xué)以致用.

