“圖形平移”以靜制動解決參數分類討論問題

武志容

摘要：帶參數的函數求值問題是近幾年的高考常考題，通常需要根據參數的情況進行分類討論，那參數怎么取值，怎么分類通常困擾了廣大的師生，有時候遇到多個參數更是不知該依照哪個參數進行分類討論好，特別是對于思維不是很靈活的學困生而言，往往會思路一片混亂導致無從下手.“圖形平移”就是通過數形結合的方式，利用圖形的平移，給參數解決鋪一條主線，沿著這條主線動態的刻畫參數變化的過程，從而找到不同狀態下對應的情況，其直觀感知的思維特點非常適合學困生掌握.

關鍵詞：圖形平移以靜制動參數學困生

“圖形平移”在課本人教版必修5《線性規劃》中有應用：

引例已知實數x，y滿足x-y+2≥0，

x+y-4≥0，

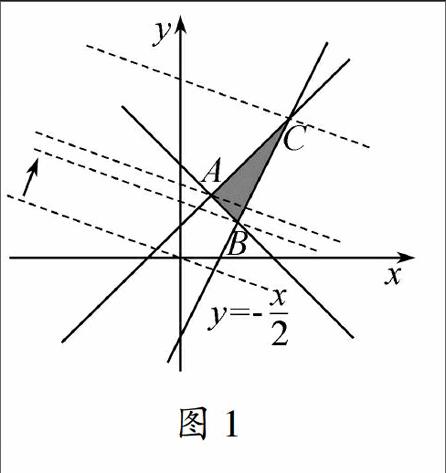
2x-y-5≤0，則目標函數z=x+2y的最大值為.

圖1解析先畫出不等式組所確定的區域范圍即△ABC（圖1），再將直線y=-x2的圖像向上平行移動穿過△ABC，顯然最大值的位置為過點C的直線.

此解法主要運用數形結合思想，這里的目標函數值z是一個參數，當這個參數取不同值時對應不同的直線方程.將這個參數通過圖像平移的方式找到它的最值狀態，從而求得它相對應的最大值.在平移的過程中特別要注意的是臨界狀態或特殊情形，這里有3個臨界點A，B，C，這3點處的靜態囊括了整個移動過程，只要抓住這3點位置就可以達到以靜制動的效果.用此方法也可以解決其他的參數分類討論問題，下面列舉幾例.1集合含參數問題

例1已知集合A={x∈R2≤x≤6}，B={x∈R2a≤x≤a+3}，若B≠且BA，求實數a的取值范圍.

解析這里有一個參數a，有兩個臨界位置2和6，a取不同的值集合B表示不同的區間范圍.哪個區間才滿足BA呢？事先不好確定.我們先畫出集合A的固定位置，再將集合B從左往右的位置平行移動，從中發現符合條件的情況：

2二次函數含參數問題

例3（2007年廣東高考21）已知a是實數，函數f（x）=2ax2+2x-3-a，如果函數y=f（x）在區間[-1，1]上有零點，求a的取值范圍.

解析標準答案的解法是根據參數a的值和零點個數來分類，其中a的值有a=0，a>0，a<0三種情形，零點有1個零點和2個零點兩種情形，其中1個零點可能是一次函數也可能是二次函數情形，由于分類情況較多，很難在短時間內分清各種情形的條件，所以學生做起來普遍感覺比較凌亂，也容易遺漏掉其中的某種情況.我們通過圖形平移來找滿足的條件，思路要順暢很多.

解先考慮特殊情形：

a=0時，x=32[-1，1]；Δ=4+8a3+a=8a2+24a+4=0時，得a=-3±72.

其中a=-3-72時，x=-12a∈[-1，1].令f（x）=2ax2+2x-3-a=0，解得x1=-1-Δ2a，x2=-1+Δ2a.

平移二次函數圖像：

1）a>0時，開口向上

解析上例函數盡管不是嚴格意義上的二次函數，是一個復合型函數，但通過求導變形后最后還是變成二次函數.這也是近幾年高考題及高考模擬題常考類型.利用圖像從左往右平移分別得到不同狀態下對應的情況，思路非常清晰、簡潔、完整、嚴密，不會遺漏掉某一種情形.這種解法非常適合學困生的思維特點，方便學困生掌握應用.下列幾例最值或取值范圍問題可用同樣方法解決：

變式1（2013年珠海高三學業質量監測20）已知函數f（x）=lnx+a-xx，其中a為常數且a>0.若函數f（x）在區間[1，2]上的最小值為2，求a的值.

變式2（2013年梅州高三總復習質檢20）已知函數f（x）=a-12x2+lnxa∈R.若在區間（1，+∞）上，函數f（x）的圖像恒在直線y=2ax的下方，求實數a的取值范圍.3圓錐曲線含參數問題

例5（2013年惠州高三第三次調研測試20）如圖7，橢圓M：x2a2+y2b2=1a>b>0的離心率為32，直線x=±a和y=±b所圍成的矩形ABCD的面積為8.

（1）求橢圓M的標準方程；

（2）設直線l：y=x+mm∈R與橢圓M有兩個不同的交點P，Q，l與矩形ABCD有兩個不同的交點S，T，求PQST的最大值及取得最大值時m的值.圖7

解（1）由題意，ca=32且2a×2b=8，所以a=2，b=1，橢圓M的方程為x24+y21=1.

（2）聯立方程y=x+m，

x24+y2=1，54x2+2mx+m2-1=0，

所以PQ=2-85m2-4×4m2-45=4255-m2.

如圖7，在原來矩形ABCD區域畫出直線y=x+m平行移動的過程，

先考慮臨界狀態情形：

當直線l與橢圓M相切時即Δ=2m2-4×54×m2-1=0，所以m=±5.

當直線l過點A（-2，-1）時，m=1；當直線l過點C（2，1）時，m=-1；

以臨界狀態為基礎，再考慮直線在平移過程中的其他狀態，按從左往右的順序分別對應：

a）當1

b）當-1≤m≤1時，點S1-m，1，點T-1-m，-1，ST=22，PQST=255-m2，所以當m=0時，PQST取最大值255；

c）當-5

綜上可知：當m=±53或0時，PQST取最大值255.

小結含參數的分類討論問題關鍵是如何分類，按照怎樣的標準或依據來分類通常是困擾廣大學子的疑團所在，圖形平移直觀形象地給出了一個分類的操作依據，將相應圖形按照一定的順序平移，從而找到相對應的不同狀態，特別是臨界狀態，往往就劃分了一個分類的標準，也往往能找到它的最值狀態及取值范圍，按此標準進行討論通常比較完整、全面，沒有遺漏，有一定的順序學生理解起來比較簡單，尤其是對學困生.新課標更側重“通式通法”的應用，圖形平移就是將動態轉化為靜態，以靜制動，用常規思路和解法來解決不常規的問題，以期達到出其不意的效果.