關于大學物理“高斯定理內容”教學的探討
2016-05-30 04:56:18江軍
教育教學論壇 2016年26期
江軍
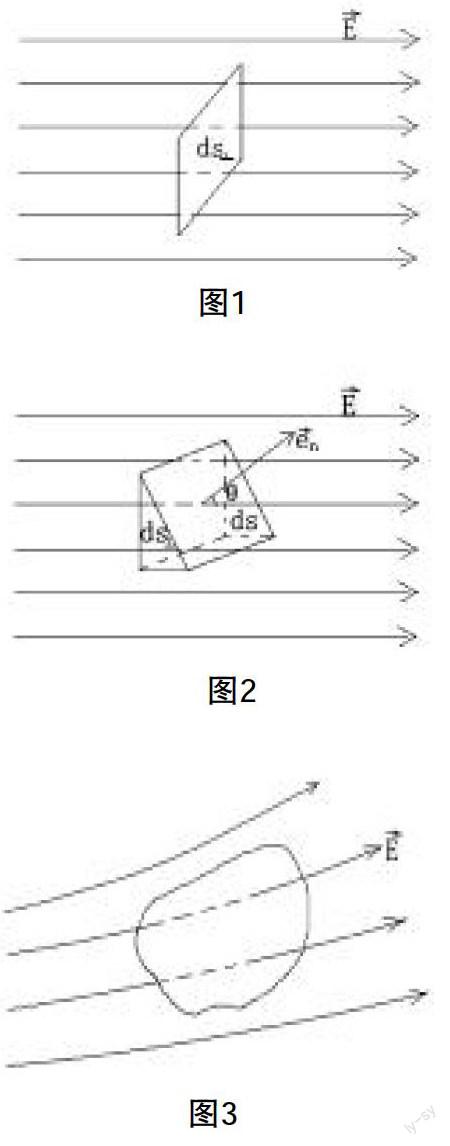
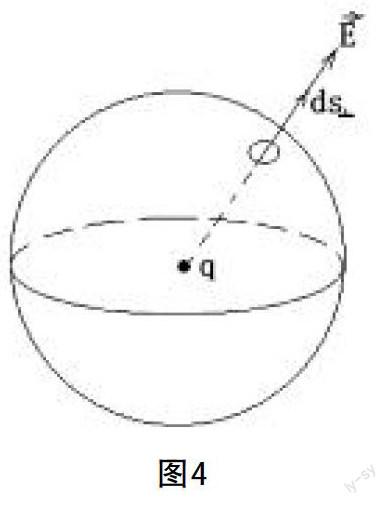
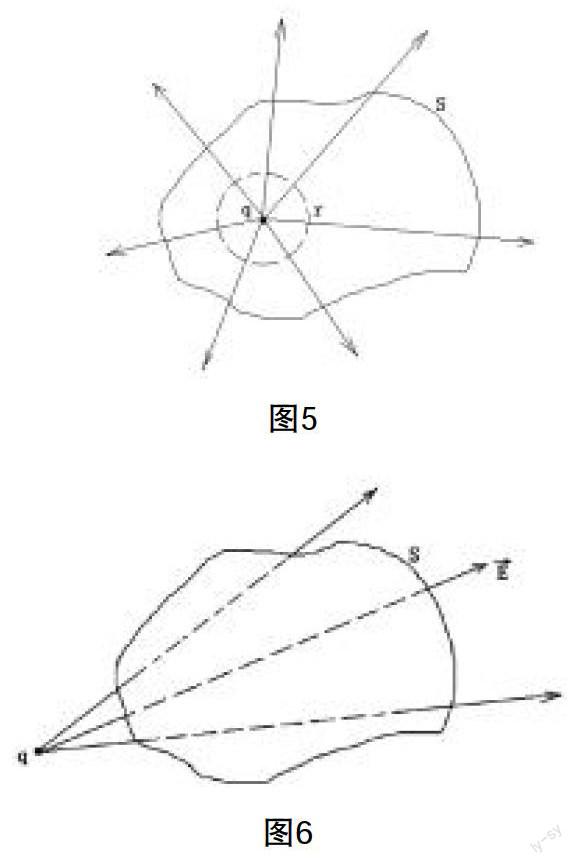
摘要:本文是關于大學物理教學中涉及“高斯定理”教學方法的一種探討,充分利用電場線的特點、電通量的概念及簡單的微積分的知識,避免大多數教材中煩瑣的數學推導,最終推導出高斯定理的結論,使學生更容易理解和掌握。
關鍵詞:電場線;電通量;高斯定理
中圖分類號:G642.0 文獻標志碼:A 文章編號:1674-9324(2016)26-0189-02
這就是著名的高斯定理的最后的數學表述,即:在靜電場中,對任一個封閉曲面的電通量等于包圍在該封閉曲面內的電荷的代數和除以真空中的電容率,與曲面外的電荷沒有關系。
這種根據電通量的概念以及電場線的性質來推導的高斯定理,避免了煩瑣的數學推導,學生更容易理解和消化。
參考文獻:
[1]籍延坤.高斯定理的數學證明[J].大連鐵道學院學報,2004,(9).
[2]付靜,姜廣軍.靜電場中高斯定理的證明[J].長春工業大學學報,2013,(02).

