水電工程初期導流標準多目標風險決策

劉國清 郭勇

摘 要：水利水電工程施工導流標準的選擇直接影響到工程的投資及安全，施工導流標準的選擇必須綜合考慮導流工程的投資、建設工期及其風險率。文章在綜合考慮施工導流多重不確定因素的基礎上給出了導流風險的計算模型，并利用TOPSIS方法建立了導流標準多目標風險決策模型。通過工程實例分析，證明風險分析方法及多目標風險決策模型是可靠適用的。

關鍵詞：施工導流；導流標準；風險；多目標決策；TOPSIS方法

1 概述

導流初期標準的選擇貫穿水利水電工程建設全過程，影響施工導流風險的因素主要有水文、水力及其它不確定性因素。導流標準越高，導流風險就越低，而投資就會越大，反之，投資就會降低，而風險會增大。

2 施工導流風險分析

2.1 施工洪水的不確定性 施工洪水過程變化受眾多因素影響，極其復雜且具有隨機性。根據壩址的實測資料，按同頻率法放大計算洪水過程線。最大洪峰流量采用P-Ⅲ典型隨機抽樣均值，其密度函數為：f（x）=（X-α）e （1）

式中：α，β，a0為P-Ⅲ型分布的形狀、刻度和位置參數；Γ（α）為α的伽瑪參數。并且有α=4C2s，β=2/（CC），α=（1-2CC）；為P-Ⅲ型分布的均值，Cv為P-Ⅲ型分布的變差系數，Cs為P-Ⅲ型分布的偏態系數。

2.2 導流建筑物泄流能力的不確定性 設計、施工等的不確定性導致泄水建筑物的泄流能力亦存在不確定性，可假定為三角分布。其分布函數為：f（x）=

式中：a為導流建筑最大泄流量；b為導流建筑物泄流量均值； c為導流建筑物最大泄流量。

2.3 其它不確定性 在設計過程中，地形資料、庫容曲線及調洪起調水位等也存在一定的不確定性。

2.4 風險率及動態綜合風險計算

2.4.2 基于Monte-Carlo方法的導流風險計算模型。由水文及水力隨機參數分別模擬洪水過程及導流建筑物的泄流能力，經過計算，得到圍堰的上游水位。根據上游水位的計算結果，可統計得出導流系統的風險率。

3 初期導流標準多目標風險決策

3.1 決策目標及其計算方法 在水電工程建設中，初期施工導流標準的選擇，除技術上可行外，還需考慮導流工程的投資、工期及導流工程承擔的風險率。處理投資、工期與風險三者之間的關系，取決于兩個方面的約束，一個是最大容許的施工進度要求，一個是最大容許投資費用的限制。對于這兩個要求的理解就是當導流發生風險時，有沒有容許的時間和費用恢復導流建筑物。因此導流標準選擇的決策指標主要有導流建筑物的投資規模（確定型費用）、圍堰施工的最大平均強度（確定型施工進度）及超載洪水導致潰堰時的風險損失（不確定型費用）。

3.1.1 導流工程投資。在導流建筑物規模確定的情況下，投資規模可以按式（5）進行估算。

3.1.2 圍堰施工的最大平均強度。圍堰施工最大平均強度D表示在考慮泄水建筑物的施工進度、截流歷時、基坑排水時間條件下，圍堰的最大平均填筑強度。

3.1.3 超載洪水導致潰堰時的風險損失。土石圍堰發生超載洪水后，假定河道具有一定的防洪能力和預防潰堰措施。在確定導流標準時，風險分析不考慮潰堰對下游的淹沒損失，只計算圍堰基坑內損失，某次超載洪水導致潰堰的風險損失可按式（6）進行估算。

式中： k為圍堰運行使用年限； i為風險損失折算成工程投資概算基準年的折現率。

3.2 初期導流標準多目標風險決策模型

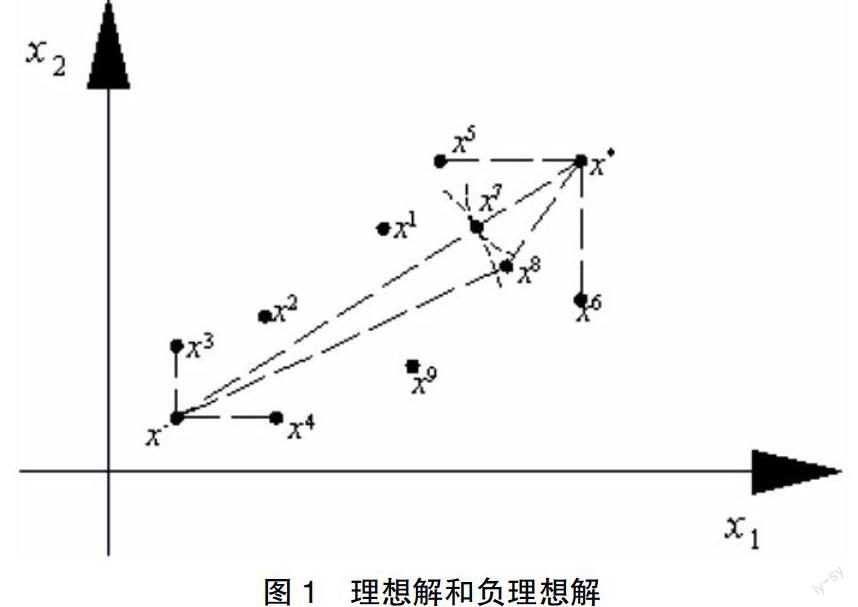
3.2.1 TOPSIS方法簡介。逼近于理想解的排序方法（Technique for Order by Similarity to Ideal Solution）[4]（簡稱TOPSIS方法）是一種借助于一多目標決策問題的“理想解”和“負理想解”去排序的方法。所謂理想解就是一設想好的最好的解（方案），它的各個屬性值都達到各候選方案中的最好的值；而一負理想解是另一設想的最壞的解，它的各屬性的值都達到各候選方案中的最壞的值。

上式中的J是效益型目標的集，J′是成本型目標集。

然后根據公式（8）～（10）計算距離S*、S-和相對接近度C*，對所有方案（初期導流標準）進行排序。

4 工程實例分析

4.1 工程概況 某水電站裝機容量2100MW，正常蓄水位高程2895m，死水位2825m，水庫總庫容39.6億m3，心墻堆石壩最大壩高315.0m，工程規模為一等大（1）型。根據《水電工程施工組織設計規范（DL/T5397-2007）》，選定的導流建筑物為Ⅲ級。對于Ⅲ級導流建筑物，土石類圍堰相應設計洪水標準為重現期20～50年。

由水文洪水資料成果可知，20～50年一遇的洪峰流量分別為QP=5%=5300m3/s、QP=3.33%=5900m3/s、QP=2%=6360m3/s。各方案上游土石圍堰高度一致，最大高度均為56.0m，均布置兩條城門洞型導流洞。不同標準對應的兩條導流洞的尺寸為13.5m×16.0m、14.0m×17.0m及15.0m×17.0m。

4.2 施工導流風險計算 根據施工組織設計資料，按照公式1～4應用導流系統風險分析方法和計算機仿真，20年、30年及50年一遇洪水時圍堰的動態風險如表1所示。

4.3 決策指標計算 根據施工總進度及概算資料，按照公式5～7進行計算，不同導流標準時的決策指標如表2所示。

4.4 各方案排序 各方案導流圍堰的施工強度一致，因此可針對不同的投資和風險權重進行方案排序的敏感性分析，應用多目標風險決策模型（TOPSIS排序方法），按照公式8～19對各方案排序值進行計算，并進行敏感性分析，然后進行方案排序，排序值最大者最優。不同權重時各導流標準的排序見表3。

4.5 計算結果分析 由計算結果可見，當投資權重大于0.8時，采用20年一遇洪水標準優于其它兩個方案；當投資權重小于0.8時，采用50年一遇洪水標準均優于其它兩個方案。因此，推薦初期導流標準為采用50年一遇洪水重現期。

5 結語

文章在分析導流標準與導流建筑物的投資、工期及風險度基礎上，根據決策目標的定量計算方法，利用TOPSIS方法建立了多目標風險決策模型。通過工程實例驗證分析，表明多目標風險決策模型是可行的、有效的。同時，還對不同的目標權重進行敏感性分析，可為不同的決策者提供更多的選擇依據。

參考文獻：

[1]《水利水電工程施工組織設計手冊編委會》.水利水電工程施工手冊（第5卷）施工導截流與度汛工程[M].北京：中國電力出版社，2005.3.

[2]肖煥雄.施工水力學[M].北京：水利電力出版社，1992.

[3]胡志根，劉全，賀昌海，肖煥雄，周宜紅，傅崢，李定葵，鄭家祥.水利水電工程施工初期導流標準多目標風險分析[J].水科學進展，Vol.13 No.5，2002（9）：634-638.

[4]陳珽.決策分析[M].北京：科學出版社，1997.

[5]肖煥雄，史精生.施工導流標準多目標風險決策[J].水利學報，1990（11）：66～71.

[6]石明華，鐘登華.施工導流超標洪水風險率估計的水文模擬方法[J].水利學報，1998（3）：30-33.

[7]肖煥雄，孫志禹.不過水圍堰超標洪水風險率計算[J].水利學報，1996（2）：37-42.

[8]肖煥雄，韓采燕，唐曉陽.施工導流標準與方案優選[M].武漢：湖北科學技術出版社，1996.

作者簡介：劉國清（1982-），男，湖北咸寧人，工學碩士，工程師。