功能關系中系統選擇對簡化力學問題重要性分析

陳志瑤 令維軍

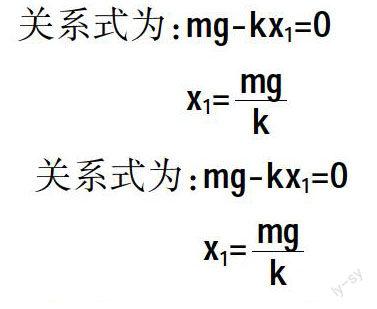
摘要：利用功能關系分析物理運動與相互作用規律是高中物理解決力學問題的常用方法，其中功能關系中系統選擇是解決問題的關鍵。本論文通過分析力學問題中的不同系統的選擇，指出正確的選擇系統，可以簡化問題，更加深入物理本質，突出物理意義，對解決力學問題具有重要的意義。

關鍵詞：功能關系；系統選擇；機械能；保守力做功

中圖分類號：G642.0 文獻標志碼：A 文章編號：1674-9324（2016）17-0117-03

在人教版普通課程標準實驗教科書必修2（2010年4月第三版）第七章中開始做功和能量問題的教學，縱觀教材可以發現，教材對能量問題的基本線——功能關系分析不夠明確，容易給初學者混亂的感覺，而功能關系是分析物體的運動與相互作用的最基本規律，也是研究物理力學問題最基本的常用方法。

一般情況下，運用能量觀點分析解決問題的基本思路，運用功能關系解決力學問題步驟的第一步就是對于研究系統的正確選定，對于高一學生的認知水平來說，要運用功能關系分析解決問題，首先要做的就是確定研究對象（即系統），這是涉及功能關系中問題分析的關鍵所在。要順利解決問題，首先要選擇恰當的研究系統，明確外界與系統之間的做功情況，通過分析外力，非保守內力和保守內力的做功，從而找出它們之間的內在聯系，更好地利用功能關系解決實際力學問題，在處理任何力學問題的過程中能夠形成舉一反三的解題思路。

一、系統選擇在功能關系中重要性的理論闡釋

在力學中，提到系統選擇我們就自然而然地想到功能關系，功能關系與能量密不可分，能量、功能關系、系統選擇之間的關系是怎樣的呢？系統選擇在功能關系中問什么這么重要呢？下面我們就三者之間的關系及重要性進行闡述。

1.物體具有能量。教材在第七章以能量問題為引子，用伽利略的理想實驗引入思考，“某個量是守恒的”，這個量就叫能量。可以看出能量概念是物理中的一個比較抽象的概念，在物理學的發展過程中，能量的概念幾乎是與人類對能量守恒的認識同步發展起來的，能量的概念之所以重要，就是因為它是個守恒量。我們知道從能量觀點分析和解決問題，需要有較高的思維起點，需要學生具有綜合運用所學知識，以及對物理過程進行全面、深入分析的能力，在高中物理教學中，指導學生學好這部分內容，使學生真正全面正確理解及熟練運用能量知識解決物理問題顯得很重要，而我們的能量又跟力學緊密聯系著，并且是引出功能關系的源頭，所以重要性就不言而喻了。

2.功能關系很重要。能量是引子，功能關系就是主干了。所謂功能關系即物體做功和能量轉化之間的關系，就是外力做的功與物體能量變化之間的關系。這在整個中學物理教學中有著十分重要的地位，也是高考必考點之一，它貫穿于力學、熱學、電磁學、光學和原子物理學各個部分。我們知道力學中的功能關系分析是第七章教材能量問題的基本線，是主干，是引導，運用功能關系的第一步系統選擇來解決力學問題成為解決該問題的關鍵所在。教材以動能定理引入功能關系（動能定理：力在一個過程中對物體做的功，等于物體在這個過程中動能的變化）[1]，動能定理的研究對象只能是單個物體，如果研究的不僅僅是單個物體而是系統，對功能原理加深理解就是外力和非保守力所做功之和等于機械能的增量[2]，可表示為ΣW外+ΣW非保內=（Ek2+Ep2）-（Ek1+Ep1）=Δ（Ek+Ep）=ΔE。如果外力和非保守力做功為零，此系統機械能守恒。

在解決力學問題上，機械能守恒定律只適用于慣性參考系，且物體的位移、速度必須相對同一慣性參考系。但在解決實際力學問題中，當外力和非保守力做功或其代數和不為零時，機械能守恒的條件是無法嚴格滿足的，這是因為物體運動時總要受到空氣阻力和摩擦力等非保守力的作用，并始終做功，因而系統的機械能要改變，但是當摩擦力等非保守力的功同機械能相比可忽略不計時仍可用機械守恒定律來處理問題。在機械運動的范圍內，我們所討論的只是機械能（或動能和勢能），可知，只有外力做的功ΣW外和非保守內力做的功ΣW非保內才會引起機械能的改變。機械能守恒定律是功能關系的特例，在這類問題中，系統選擇很重要。

3.功能關系系統選擇的重要性。我們知道，要解開一團線，找到線頭是極為重要的。要功能關系簡潔地解一道力學題，第一步最重要。運用功能關系解決力學問題的第一步就是對于研究系統的正確選定，這是功能關系中問題分析的關鍵所在。要順利解決問題，首先要選擇恰當的研究系統，明確外界與系統之間的做功情況，通過分析外力、非保守內力和保守內力的做功，從而找出它們之間的內在的聯系。這樣就能快速、正確、簡潔地解決你需要解決的問題。

以上分析可以看出，能量、功能關系、系統選擇之間的關系環環相扣，缺一不可。正確地選擇系統，可以避免很多的不必要的麻煩，盡量選擇包含保守力的系統，這樣保守力做功可以直接通過勢能變化量來表示，使功能關系的表達式物理意義更加清楚明了。同時有利于問題的簡化，更加突出物理意義，這對于我們用物理思維解決力學問題有導航的意義和作用。

為了加深對功能原理系統選擇的深入理解，我們通過具體實例來說明如何運用功能原理解決力學問題。

二、系統選擇在功能關系中的案例解析

案例1：如圖1所示，一個勁度系數為k的彈簧上端固定，下端掛了一質量為m的物體，先用手托住，使彈簧保持原長。設x軸向下為正，取彈簧原長處為坐標點o。

若將物體拖住緩慢放下，到達靜止時，彈簧的伸長量x1是多少？

若將物體突然放手，物體到達最低位置時，彈簧的伸長量x2是多少？

分析：研究對象是一個系統，當選擇系統的不同，所列出的關系式包含的意義也不同，我們以下列所選的系統舉例列出以下列物體為系統時的功能關系式：

1.m，k，地球；2.m，地球。

（1）由于是緩慢放下，物體在整個下落過程中可以近似為是受力平衡的。

①以m，k，地球作為系統。在下落的過程到達o點（平衡位置）時靜止，在這個狀態下物體（外力）不做功，這時m只受到豎直向下的重力和豎直向上的彈力，它們在這里只扮演內力的角色。

②以m，地球作為系統。靜止時，重力是m的內力，因為平衡，彈力在這個系統充當了外力。

小結：以m，k，地球作為系統時，在靜止狀態下物體（外力）不做功，這時m只受到豎直向下的重力和豎直向上的彈力，要給高一的學生區分外力在這個時候是一個內力的角色是不容易的，他們的物理知識容量還沒有達到那個層次，很容易和之前的知識點產生混亂。

在選擇以m，地球作為系統的過程中，重力主要是地球吸引力的作用下所產生的，在這個系統中的重力是一個內力，高中一年級的學生已經學過重力是保守內力知識點，不用過多的解釋，不容易造成混亂，因此，在這個系統中理解這個案例的問題以及解題思路和所列出的關系式比較容易讓讀者（學者）接受。

（2）設彈簧原長處于重力勢能和彈性勢能的零點，且此時物體靜止，因此，該狀態系統機械能為零。

①以m，k，地球作為系統。突然放手，這時系統機械能守恒，系統在m下落的過程中彈力這個外力做功和非保守內力重力做功都為零，機械能為零，以o處為零勢能點，根據機械能守恒，最低位置靜止狀態，動能為零，兩狀態機械能相等。

當以m，k，地球作為系統。突然放手，動能和勢能相互轉化，在物體運動的過程中系統機械能守恒，機械能為零，靜止狀態，動能為零，兩位置點機械能守恒。在這個系統中很容易理清運動關系得出精確的關系式。而以m，地球作為系統靜止時，左邊，彈力就要充當外力的角色，并且外力做了功，等于右邊動能的變化，而右邊是靜止，動能為零，重力為保守力，機械能的增量，關系式可以列出來，但這個關系式用物理理論是不可以相等的，是說不通的。因此，合理地選擇系統很重要。

案例2：如圖2所示，在水平桌面上放在質量為M的木塊，M的一端與勁度系數為k的輕彈簧相連，并固定在墻上，另一端經輕滑輪與下垂的重物質量為m的C相連，設M與桌間摩擦系數為μ，其余為光滑接觸，開始時M靜止于平衡位置，求當m下降距離為d的速率為ν有多大？[2]

分析：這個題目整個系統包含了重力、彈力、摩擦力做的功及機械能的變化，我們以下列所選的系統舉例列出以下列物體為系統時的功能關系式：

1.M，m；2.M，m，k，地球；3.M，m，k；4.M，m，地球。

根據功能原理和題目所要求的四類系統，可分別得出如下關系式：

①以M和m作為系統，在整個運動過程中，內力和外力的確定與所選取的系統有關，顯然在這個系統中重力、彈性力均為外力，摩擦力做的功可視為系統的外力負功，可得到外力做功之和等于機械能的增量。

②當以M、m、k和地球作為系統時，我們發現這時候的重力和彈性力以內力的角色出現，外力就只有摩擦力，可得到摩擦力做的功就等于整個機械能的增量減去內力做的功。

③當M、m、k作為系統時，這時系統外的重力和摩擦力顯然是外力，我們知道外力做的功等于機械能的增量減內力做的功，由題目可知彈性內力做的功是負功。

④當M，m，地球為參考系，也就是把重力就作為內力，這個時候彈性力，摩擦力做的功就是外力做功。

在這里我們需要注意的是，系統內保守力做的功的量值與其相應的勢能增量是相同的，在功能關系中決不可重復計入。如④式中，重力作為內力角色其勢能變化已在等式右方考慮，等式左方就不得計入，并且彈性力作為外力做功已在等式左方考慮，等式右方就不得重復入內。

從以上分析中，將M，m，k，地球看作一個系統物理意義更加明顯，系統中重力和彈力變為內力，由于它們為保守力，其做功可以通過重力勢能和彈性勢能的改變來表征，系統只有摩擦力為外力，其做的功可以表達為整個系統機械能的增量。使表達表達更加清楚明了，避免了重力和彈力做功的重復計入的混亂。

三、小結

在人教版普通課程標準實驗教科書必修2（2010年4月第三版）中可知機械能守恒定律只適用于慣性參考系，如果系統選擇不同，在一個系統適用的機械能守恒定律在另一個系統中則不一定機械能守恒，通過以上案例，我們可以看出，以不同的系統為參考系，則作用力的性質是不同的，在一個系統中的內力在另一個系統中可能為外力，表達式中這個力作用的涵義就不同。教師在講解力學中功能關系問題（適用于高中一年級學生）時，在系統完全確定后，等式左面部分代表外力和非保守力做的功，右面為機械能的增量。因此系統的選擇直接影響功能關系的表達式，我們在選擇系統時，盡量選擇包含保守力的系統，這樣保守力做功可以直接通過勢能變化量來表示，使功能關系的表達式物理意義更加清楚明了。同時有利于問題的簡化，更加突出物理意義。

系統的選擇，對應了不同的功能關系，深刻理解系統選擇，對很好地理解功能關系以及發散思維是很有優勢的，因此在解題過程中教師可以適當擴展，指出系統選擇的重要性。

參考文獻：

[1]普通高中課程標準實驗教科書·物理（必修2）[M].北京：人民教育出版社，2010：101.

[2]王少杰，顧牡.新編基礎物理學[M].北京：科學出版社，2012，（6）：37-53.

[3]陳震.功能關系及常用的八種表達式[J].理科考試研究綜合版，2013-09-1：50.

[4]余俊文.淺析去”功能關系”后的兩個瑕疵[J].教學與理論，2013-11-1：82-83.

[5]朱偉華.能量教學的基本線——功能關系（對人教版高中物理教材處理功能關系的探討）[J].實驗教學研究 實驗教學與儀器，2010，（6）：75.