線性代數的教學策略與學習方法
仇昌榮 姜岳道
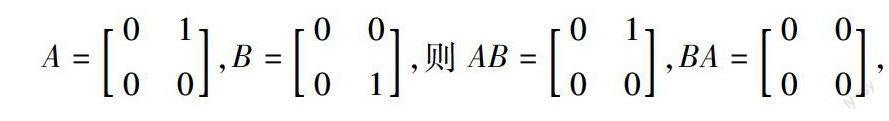
【摘要】線性代數抽象難懂,在大學校園中存在著厭學現象.本文指出了在教學過程中只有從線性代數課本身的特點和學生的實際能力出發,加強基本概念的教學,使學生明確概念內涵,才能真正學會線性代數.本文也指出了邏輯推理能力得重要性,良好的邏輯推理能力使知識點銜接、成網.同時注意數學學習方法的總結,這樣才能取得良好的效果.
【關鍵詞】線性代數;概念;教學;學習方法
《線性代數》是普通高校的一門基礎理論課程,通過本課程的學習使學生掌握線性代數的基本概念和基本定理.線性代數有著重要應用,計算機圖形學、計算機輔助設計、密碼學、虛擬現實等技術無不以線性代數為其理論和算法基礎的一部分.線性代數具有高度的抽象性和嚴密邏輯性,但是缺乏直觀的數學模型.線性代數課時短、內容多、理論多,例題少,它經常開設在大一.這些令學生普遍感到學習線性代數困難.除了上述的原因外,它也與教師的教學經驗、教學方式、教學策略、對教材的處理方法等因素有密切關系.為了解決這個問題,筆者認為,可以從以下幾方面入手.
一、加強基本概念的教學
在線性代數學習中,定義、定理及其推論等基本概念是我們做題的基礎,只有深刻地理解定義、定理隱藏的知識,才能更好地把握定理及其推論的應用.我們在教學中,不能要求學生死記硬背公式,要想辦法讓學生理解這些概念、公式.怎么做呢? 就是盡量將概念具體化,如何具體化呢?盡量給予事例說明.如矩陣、線性變換、特征值與特征向量,讓學生記住具體事例,使之認識深入化.在引導學生學習某些有具體幾何背景(向量的模)的概念時,讓學生多加聯想,指導學生按圖索驥.
為了讓學生吃透概念,授課時應該提醒學生注意兩方面的問題:1.對概念、定理的陳述如果是嚴謹的,那么就要一字一句的摳,一個字都不能動,改動個別字就會導致題意發生根本變化(線性相關、線性無關的概念);2.對于有些概念、定理,自己能夠簡明扼要用自己地語言來描述它們.另外,在教學中還可適當的構造反例,使學生加深對概念的理解,例如數的乘法運算滿足交換律和消去律,但矩陣的乘法運算不滿足交換律和消去律,這樣的反例,直觀性強,淺顯易懂,能給學生留下深刻的印象,使學生掌握概念的本質.既提高了學生分析問題和解決問題的能力,又加深了學生對基本基本知識點的理解,為學生后續課程的學習打下了堅實的基礎.
二、強化邏輯推理能力訓練
邏輯推理是數學的一個基本功能,它也是人們學習和生活中經常使用的思維方式.邏輯推理能力是學好線性代數必須具備的能力,只有具備了良好的推理能力,才能做到既合理猜想又大膽猜想,敢于突破常規思維定式,但是邏輯推理能力的形成和提高是一個緩慢的過程,短時間內很難見效果,我們要創設概念、定理、方法等問題的活動情境,將抽象的理論想辦法具體化,讓學生自己探究知識、形成結論.這樣我們既鍛煉了他們的推理能力又培養了他們的學習興趣,不再覺得學習線性代數是乏味、無趣.推理能力的培養,要考慮學生的自身特點、層次性,思維方式也存在著一定的差異,我們要因人施教,因材施教,這樣使學生的邏輯推理能力不斷躍上新臺階.線性代數的知識點較多,很多重要概念之間的內在聯系并沒在課本中充分反映出來.學生只有具備良好的合情推理和演繹推理能力,才能掌握知識點的核心.例如,向量的線性組合與線性方程組的解、向量的線性相關與齊次線性方程組的非零解均關系密切,但教材中把它們放在不同的章節,很少有學生考慮這些概念之間的聯系,在這些教學內容完成后,我讓學生自己推理出這些概念之間的關系,結果許多學生自己找到了正確的答案.
另外,還要讓學生注意新舊知識的聯系,最后把同類知識歸納、總結、列表,把容易混淆的概念進行對比,以加強學生的想象力、理解力、記憶力.對于有些習題,還要注意一提多解及同類題的共性,培養舉一反三和推理能力.
三、注意學習方法的總結
線性代數的概念很多,重要的有:逆矩陣,初等變換與初等矩陣,正交變換與正交矩陣,特征值與特征向量.運算法則也很多,重要的有:矩陣乘法,求矩陣的秩,求非齊次線性方程組的通解,基本運算與基本方法要過關.這些知識點從內容上看環環相扣,相互交錯.要使知識點銜接、成網,歸納總結是不可缺少的步驟.我們對問題的表述要富有邏輯性,解題方法靈活多樣性.在復習時常問自己做得對不對?再問做得好不好?只有不斷地歸納總結,努力搞清內在聯系,使所學知識才能融會貫通,解題思路自然就開闊了.
布置作業時,教師應對計算題有所選擇,一般不宜讓學生考研、未知量多、參數復雜等計算量很大的題目,作業目的主要在于理解和鞏固知識,否則會造成學生有限學習時間的浪費,會挫傷學生的學習線性代數信心,得不償失.
總之,只要在線性代數課堂中,教師采取恰當的教學策略,即注重基本概念的講解,進行概念、公式的推理能力訓練,并注重數學學習方法的總結,就一定能取得良好的教學效果.

