處理數學作業的有效策略
葛家華
摘要:當代美國數學家哈爾莫斯說過:“數學真正的組成部分應該是問題和解,問題是數學的心臟。”仔細揣摩,的確,在數學教學中,解題活動是最基本的活動形式。
關鍵詞:數學作業;處理;有效策略
中圖分類號:G633.6 文獻標識碼:A 文章編號:1992-7711(2016)06-0084
幾乎每節數學課,教師都會布置作業。數學教學往往通過作業,以達到對知識的鞏固、加深理解和學習運用,從而形成技能、技巧,以及發展智力與解決問題的能力。數學作業質量的高低往往可以衡量一個學生的數學學習水平。學好數學,還要學會聰明地做題。既要在做題的實踐中加深理解、增長才干,又不為其所累。怎樣才能“聰明地做題”呢?
一、掌握步驟,正確解題
解數學題,一般有以下八個步驟:審題→畫圖→分析→解題→檢查→討論→答題→小結。
1. 審題。題目本身是“怎樣解這道題的鑰匙”,只不過其中的積極提示往往是通過文字語言、公式符號以及他們之間的聯系間接地告訴我們。所以拿到題目,先不要急忙做題,應該先認真閱讀,弄清題意:(1)這是什么類型的習題?是選擇題、填空題、求解題、作圖題,還是證明題?(2)已知哪些條件,需要求什么?要求的是幾個問題?即使問題再簡單的題目,也少不了這一步。如安徽省2012年中考題第16題解方程:x2-2x=2x+1,問題很簡單,當你看到題目后,時間很短明確它是解一元二次方程問題,實際上就是審題的過程。
2. 畫圖。解幾何題,畫圖往往是不可少的,由題設畫出符合條件的圖形,標上已知或未知的元素。如有關行程問題、求一些事件的概率問題也常常需要畫示意圖或列適當表格,以幫助理解。相關函數問題,有時也需要畫出函數的圖像。正確的圖表,有助于更深刻地分析題意,找出解題思路。
3. 分析。所謂“分析”,就是分析解題思路,找到解題的方法,這是整個解題中最困難的一步。如果題目思路明確,可以用順推法,直接由已知條件出發,逐步按題目的要求推導下去。如果思路不明確,可以“先逆后順”,即先假設結論已得到,逐步向上逆推,溝通渠道后再順推下來。通常分析問題,是采用“雙向推法”,順逆綜合進行,直到溝通為止。對于幾何證明題,一般采用“執果尋因”的分析方法。
4. 解題。關于解題:這一步就是把解題思路轉化為具體的解題步驟,并且按順序書寫下來。解題步驟不能跳躍,主要步驟不能省略,要使別人看得懂,重要的依據要寫出來。例如,學生利用“射影定理”解決問題必須指明,推而無理、算而少據的壞毛病要克服。書寫要整齊清晰,一般一式一行、等號對齊、符合數學書寫要求。
5. 檢查。題目解出后,還需要檢查解答:(1)檢查解題過程是否有無;(2)檢查是否按照問題的要求的順序作答,是否回答了全部問題;(3)檢查答案是否符合題意,如方程問題,檢查有無增失根的情況。
6. 討論。有些問題在某種情況下有解,某種情況下無解;在有解的情況下,何時只有一解,何時有無窮多個解,遇到這種情況,需要對題目進行討論。如:
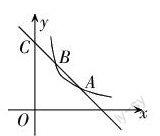
如圖,函數y1=k1x+b的圖像與函數y2=的圖像交于點A(2,1)、B,與y軸交于點C(0,3)。
(1)求函數y1的表達式和點B的坐標;
(2)觀察圖像,比較當x>0時y1與y2的大小。
【解】
(1)思維要活,格式要“死”
思維要活,說的是靈活地運用各種知識巧妙地解答數學題,這是數學作業的較高要求;格式要“死”,說的是解題格式要正規,要有合乎數學特點的標準格式,敘述清楚,推理嚴謹、計算準確、解答完整,這是數學作業的基本要求。每年的數學考試,都有不少學生因解題格式不規范而被扣分的,應該引起我們的注意。
例如,解方程(組)、不等式(組)等,每一步都有一定的格式要求,學生必須按照這種格式進行解題。但在具體解題時,還應該根據問題的特殊情況靈活解題。如下面的二元一次方程組198x-163y=1163x-198y=-1,若直接用代入消元法或加減消元法都較為繁瑣。
(2)限時作業,提高速度
提高解題速度,是數學作業的一項基本功,一些學生考試時感覺到時間不夠用,這與解題速度慢有關。因此,我們平時要有效率感,在單位時間內增大勞動量。
學生若平時做作業一般需45分鐘,能否讓他們給自己一個指令:今天作業,節約1秒,學生去做了,結果會發現,節約的可能不止1秒,也許是幾分鐘,經常進行限時作業,對提高解題速度大有好處。
(3)有錯必糾,彌補缺漏
做數學作業,難免會出現一些錯誤。錯誤的存在,反映了學生在學習中存在的問題。對于作業中的錯誤,一定要做到認真分析,找出原因,及時糾正;比較嚴重的錯誤,可以借鑒一些優秀學生的做法:如準備一本《錯題集》,全部記錄在《錯題集》里,把各種錯誤按類型進行歸納,并附上正確的解答,經常翻閱,這樣在以后的作業和考試中,就不再犯以前的錯誤了。
(4)一題多解,一題多變
一道數學題,往往有多種解法。一題多解既能使我們廣泛地、綜合地運用基礎知識,提高基本技能,更有效地發揮邏輯思維,提高全面分析問題的能力,找到最簡潔的解題途徑,又能增強我們學習數學的興趣。
一題多變。“做一題,解一類”,可以幫助我們拓寬數學基礎知識,提高解題能力。如滬科版教材中的八上學習等腰三角形時經常會遇到這樣的問題:
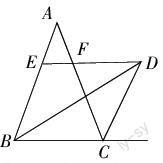
問題一:已知,如圖所示,BO、CO分別平分∠ABC、∠ACB,過點O作EF∥BC,求證:EF = BE + CF
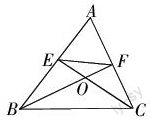
問題二:已知,如圖,△ABC的∠ABC的平分線BD與∠ACB的外角平分線交于D點,DE∥BC交AB于E,交AC于F,求證:EF=BE-CF。
對兩題的證明進行分析,不難發現,等腰三角形的判定,對于完成兩題的證明,都起了重要作用。因而,是不是可以把“圖形中存在角的平分線,又存在一條和角一邊平行的直線時,應立即找出必然存在的一個等腰三角形”作為一條思考規律,這就是舉一反三,當我們解完這些問題后,便會發現:異圖同解,各盡其妙,不變中有變,變中有不變。那就需要我們注意小結,探索規律。當我們解完數學題后,應考慮能否從這些數學題中獲得有益的啟示。
荷蘭著名數學家和教育家費賴登塔爾指出:“反思是數學思維活動的核心和動力。”學生解題后,通過對解題活動的回想,深究數學解題活動中所涉及的知識、方法、思路、策略等,改進和完善解題步驟,活躍思維,提高分析問題和解決問題的能力,最終提高學習效果。可見,培養學生的反思意識和能力非常重要。
(作者單位:安徽省合肥市南崗中學 230000)

