尺寸精度的灰色預(yù)測(cè)模型研究

韓興國(guó)　崔學(xué)峰

摘要：在工件加工過(guò)程中影響尺寸精度的因素很多，有些因素是隨機(jī)的、無(wú)規(guī)律的，是一個(gè)灰色量，因此文章通過(guò)建立GM（1，1）模型對(duì)尺寸精度進(jìn)行預(yù)報(bào)。而考慮到外界因素對(duì)系統(tǒng)的擾動(dòng)，使得數(shù)據(jù)存在失真的可能，以此引進(jìn)緩沖算子的概念，與原始數(shù)據(jù)建立的模型的預(yù)測(cè)值進(jìn)行比較，判斷是否存在數(shù)據(jù)失真的可能，保證預(yù)報(bào)精度。

關(guān)鍵詞：尺寸精度；灰色模型；緩沖算子

1 引言

機(jī)械產(chǎn)品加工過(guò)程中影響尺寸精度的因素很多，其中的主要影響因素：原始誤差，機(jī)床誤差，刀具誤差是沒(méi)辦法測(cè)量的，所以機(jī)械加工過(guò)程是個(gè)典型的灰色過(guò)程。

灰色模型就是應(yīng)用數(shù)理統(tǒng)計(jì)知識(shí)和建模理論，根據(jù)已知的少量信息進(jìn)行建模，減弱系統(tǒng)的隨機(jī)性。由于隨時(shí)間變化的因素太多，使得機(jī)械加工尺寸有時(shí)變性。要想機(jī)械加工尺寸有較為準(zhǔn)確的預(yù)報(bào)，就需要模型能考慮外界環(huán)境對(duì)尺寸加工的影響，使得模型能對(duì)加工系統(tǒng)及時(shí)做出正確的反應(yīng)。在傳統(tǒng)灰色模型的基礎(chǔ)上，通過(guò)指數(shù)型弱化算子的構(gòu)造弱化外界環(huán)境對(duì)原始數(shù)據(jù)失真的干擾，以此優(yōu)化預(yù)報(bào)模型的預(yù)報(bào)精度。

2 GM（1，1）模型的建立

灰色預(yù)報(bào)模型主要是通過(guò)先建立原始序列，對(duì)原始序列進(jìn)行一次累加生成累加序列，通過(guò)最小二乘法求出參數(shù)的計(jì)算公式，以微分方程作為演繹推理工具等，得到時(shí)間響應(yīng)序列函數(shù)，然后對(duì)模型進(jìn)行理論和實(shí)驗(yàn)分析，對(duì)尺寸精度進(jìn)行灰色預(yù)報(bào)。

2.1 試驗(yàn)準(zhǔn)備

試驗(yàn)時(shí)使用的車(chē)床為C5112A型數(shù)控單住立式車(chē)床，內(nèi)圓直徑尺寸為mm的進(jìn)油環(huán)，通過(guò)實(shí)驗(yàn)觀察在連續(xù)加工過(guò)程中車(chē)削加工的尺寸偏差的趨勢(shì)性和隨機(jī)性，發(fā)現(xiàn)機(jī)械加工過(guò)程對(duì)加工尺寸的影響規(guī)律。

2.2 試驗(yàn)數(shù)據(jù)

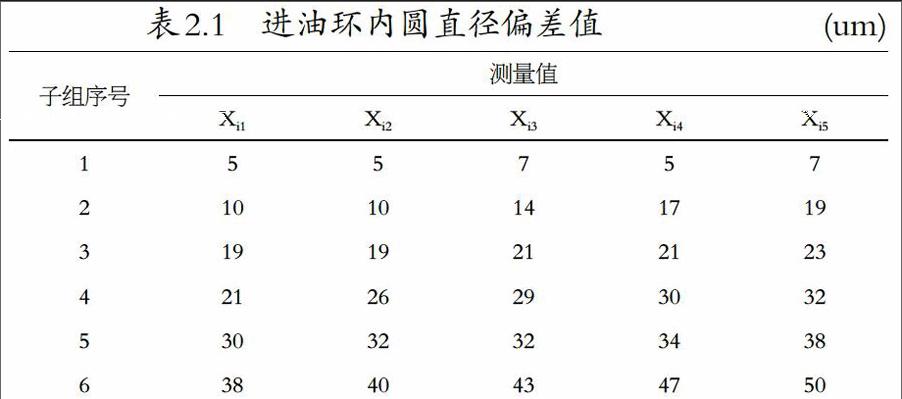
取直徑尺寸偏差為預(yù)報(bào)對(duì)象，以進(jìn)油環(huán)內(nèi)圓直徑尺寸的偏差值為建模的序列，建立GM（1，1）模型。偏差值見(jiàn)表2.1

2.3 試驗(yàn)過(guò)程

試驗(yàn)步驟如下：

第一步建立原始序列。將表2.1中的原始數(shù)據(jù)以6個(gè)為單位代入時(shí)間序列GM（1，11模型，設(shè)進(jìn)油環(huán)內(nèi)圓直徑尺寸變量X^（0）={X^（0）_（i），i=1，2，…，n}。

第二步建立累加序列。對(duì)X^（0）進(jìn)行一次累加生成一次累加序列：X^（1）={X^（1）_（K），K=1，2，…，n}=（5 10 19 21 30 38}

第三步生成微分方程。GM（1，1）模型相應(yīng)的微分方程為

+ax^（1）=μ （式2.1）

式中：a為發(fā)展灰數(shù)；μ為內(nèi)生控制灰數(shù)。

第四步利用最小二乘法求解。即可得預(yù)測(cè)模型

+1）=37.43.14 （式2.4）

用式2.4即可算出預(yù)測(cè)值如表2.2所示

3 精度優(yōu)化

引入緩沖算子，優(yōu)化模型精度。首先對(duì)原始數(shù)據(jù)序列進(jìn)行一階弱化處理，建立基于弱化緩沖算子處理后數(shù)據(jù)序列的生成模型，將生成模型還原成原始數(shù)據(jù)模型進(jìn)行預(yù)測(cè)從而起到弱化數(shù)據(jù)失真的作用，優(yōu)化模型預(yù)測(cè)精度。

3.1 指數(shù)型弱化緩沖算子的構(gòu)造

基本概念：設(shè)X^（0）=（X^（0）（1），X^（0）（2），……，X^（0）（n））為系統(tǒng)真實(shí)行為序列，而觀察到的系統(tǒng)行為數(shù)據(jù)序列為X=X^（0）（1）+ε₁，X^（0）（2）+ε₂，

……，X^（0）（n）+ε_n=X^（0）+ε，其中ε=（ε₁，ε₂，……，ε_n）是n個(gè)沖擊擾動(dòng)組成的數(shù)據(jù)序列，稱(chēng)x為沖擊擾動(dòng)序列。

弱化緩沖算子序列的構(gòu)造：設(shè)為系統(tǒng)行為特征序列，且令緩沖序列XD₁=（x（1）d₁，x（2）d₂，……，x（n）d₁），

x（k）d₁）

則當(dāng)X為單調(diào)序列（不論增長(zhǎng)或衰減）或振蕩序列時(shí)，D₁、D₂、D₃、D₄皆為弱化緩沖算子。

對(duì)原始數(shù)據(jù)序列x=（5 10 19 21 30 38），利用一階k次平均弱化緩沖算子，將原始數(shù)據(jù)進(jìn)行一階弱化處理，處理后利用GM（1，1）模型分別對(duì)緩沖作用序列建模。經(jīng)緩沖算子D₁、D₂、D₃、D₄作用后的弱化緩沖序列分別為XD₁、XD₂、XD₃、XD₄，相應(yīng)的分別建立GM（1，1）模型，可得預(yù)測(cè)模型為：

+1）=35.43.15

+1）=32.13.05

+1）=30.73.12

+1）=31.63.13

通過(guò)模型所得預(yù)測(cè)值與原始數(shù)據(jù)建立的模型所得預(yù)測(cè)值的相對(duì)誤差如表3.1：

從圖中數(shù)據(jù)可以看出，預(yù)測(cè)值相對(duì)誤差比較小，表明外界擾動(dòng)因素對(duì)原始數(shù)據(jù)失真的影響較小，預(yù)測(cè)模型對(duì)精度反應(yīng)準(zhǔn)確，同時(shí)，說(shuō)明在模型預(yù)測(cè)中可以引入緩沖算子，當(dāng)數(shù)據(jù)存在失真狀態(tài)時(shí)，修正模型精度。

4 結(jié)論

4.1 運(yùn)用灰色預(yù)測(cè)模型，對(duì)改進(jìn)后的生產(chǎn)過(guò)程進(jìn)行預(yù)測(cè)。灰色預(yù)測(cè)模型能考慮外界環(huán)境對(duì)尺寸加工的影響，使得模型能對(duì)加工系統(tǒng)及時(shí)做出正確的反應(yīng)。

4.2 引入弱化緩沖算子，優(yōu)化模型精度。通過(guò)試驗(yàn)建立的模型可以用來(lái)預(yù)測(cè)尺寸精度，減少生產(chǎn)過(guò)程中的調(diào)試次數(shù)，但加工過(guò)程中對(duì)工件的影響因素具有時(shí)變形和動(dòng)態(tài)性，一些數(shù)據(jù)序列的波動(dòng)差異性比較顯著，為了建模后得到的模擬誤差相對(duì)較小，引入弱化緩沖算子，優(yōu)化模型預(yù)測(cè)精度。