奔福德定律與舞弊審計

【摘 要】 奔福德定律（Benfords Law）是早在1881年就被偶然發現的一個古老而奇妙的數學定律。該定律揭示了序數0—999在不同數位上出現的概率分布規律。文章在簡述這一古老數學定律的發展歷程與基本內容的基礎上，利用 “人為造假”的樣本數據與隨機數樣本數據對該定律進行測試，證明了奔福德定律在舞弊偵測方面的有效性，并就該定律以及與之相關的數值分析技術在我國的運用等問題談了看法，認為奔福德定律在識別“人為造假”數據方面具有明顯作用，可以將奔福德定律及其相關的數值分析工具視為“財務舞弊檢驗器”，將其納入我國的審計理論與方法體系，豐富我國在現代信息技術環境下應對高智能財務舞弊與經濟犯罪的偵測手段。

【關鍵詞】 奔福德定律； 舞弊審計； 測試； 虛假數據； 隨機數

中圖分類號：F233；D918.95 文獻標識碼：A 文章編號：1004-5937（2016）12-0007-09

引 言

近年來經濟領域的犯罪與舞弊問題在我國日趨嚴重，對這些問題的查證需要不斷完善與發展舞弊審計技術與手段。在各種舞弊審計與審計的方法中，分析性復核被認為是最為重要的工具。但是目前審計人員能夠使用的分析性復核方法極為有限，主要局限于趨勢分析、比率分析等傳統方法，這些方法在應對日益隱蔽與高智商化的財務舞弊時常顯出不適應的方面。奔福德定律在舞弊偵測領域的運用被認為是分析性復核方法在現代信息技術環境下有益的補充，因而結合我國的實際情況對其進行深入研究具有重要的現實意義。

在過去的半個多世紀中，國外大約有150篇與奔福德定律相關的學術論文發表。特別是自從美國審計準則公告第99號（SAS 99）[1]發布以來，越來越多的研究者開始關注奔福德定律在舞弊審計領域運用及其相關實務問題的解決。比如有文獻報告了如何運用奔福德定律的理論檢測在交易數據中隱藏的舞弊[2—3]；如何有效運用奔福德定律在會計數據中偵測舞弊的思路與方法[4]；如何將奔福德定律作為數值分析技術與分析性程序相結合提高注冊會計師查證舞弊的技能的問題[5—6]。隨著計算機輔助審計技術的快速發展，探討如何將基于奔福德定律理論的數值分析技術嵌入計算機輔助審計軟件以及如何借助于軟件工具進行舞弊審計成為新的熱點[7]。

在國內，迄今為止可以檢索到十多篇有關奔福德定律及其應用的論文。其中《奔福德定律：一種舞弊審計的數值分析方法》[8]是最早將奔福德定律介紹到國內的論文之一，該文除了介紹這一定律給國內讀者以外，還利用2003年1 394家上市公司公布的財務數據對奔福德定律進行了驗證性測試。張蘇彤和唐智慧[9]的《信息時代舞弊審計新工具：奔福德定律及其來自中國上市公司的實證測試》進一步對1 447家上市公司公布的2006年度的財務數據進行了驗證性分析，并且對已經被證實實施了會計造假的上市公司的會計報表數據進行了測試，提出了以奔福德定律測試過程中形成的“相關系數”可以作為“財務舞弊測試器”的觀點。近年來國內發表的相關論文主要還停留在科普性的介紹與理論上的測試與探討層面[10]，僅有少部分論文論及奔福德定律的舞弊檢測方法[11]以及運用奔福德定律的理論對上市公司的虛假會計報表、財務舞弊等問題進行實證分析[12—13]。總體來看，我國對奔福德定律及其在舞弊審計領域的運用還處于理論上探討與科普性介紹階段，缺乏對策。

本文的主要貢獻在于首次運用“人為造假”樣本數據與隨機數樣本數據對奔福德定律進行了全面的測試，證明了奔福德定律在舞弊識別上的有效性。

一、奔福德定律：描述序數在不同數位上概率分布的奇妙數學定律

（三）適合奔福德定律數據的條件

并非所有的數據都符合奔福德定律，符合奔福德定律的數據一般應滿足以下條件[19]：

1.數據應該是以某種方式涉及或從屬于某種現象，換句話說，是由于某種原因（某一現象或事件）而導致發生的數字。比如，股票價格的形成要受到股票市場、與經濟和金融環境有關的競爭力影響。

2.數據沒有最大值或最小值的限制，比如人的年齡、人的體重、人的身高、田徑運動員100米跑的成績、小時工資額等。

3.數據完全應該是自然發生，不能是人為預先安排有特定含義的數字，如電話號碼、身份證號、股票代碼、社會保險號等，也不能是人頭腦中想出來的數字，如ATM自動取款機上的取款金額。

4.數據既不能是完全隨機數，也不能是有規律的數列。

5.數據的形成受多種因素綜合作用，尤其適合分別來自兩個以上系統的數據再經過一定運算后形成的數據。

二、對奔福德定律的實證測試：基于“人為造假”與隨機數樣本數據

（一）樣本數據及其來源

為了加深對奔福德定律的認識，全面了解“人為造假”數據的統計學特征，并驗證奔福德定律在識別財務舞弊方面的有效性，筆者利用近年來面對面給各類學員授課的機會先后請了321名學員以財務造假者的心態書寫了6組總數為9 630個“人為造假”數據，這些數據的收集情況見表1。

為了進行對比分析，筆者利用Excel 2007的隨機數發生器，運用函數“RANDBETWEEN（BOTTOM，TOP）”分別在100—999、100—9 999、100—99 999、100—999 999、100—9 999 999和100—99 999 999的范圍內生成了6組，每組5 000個隨機樣本數據。這些數據的情況見表2。

（二）測試假設

假設1：“人為造假”樣本數據的首位數、第二位數、前二位數的概率分布與奔福德定律理論值存在顯著差異；

假設2：隨機數樣本數據的首位數、第二位數、前二位數的概率分布與奔福德定律理論值存在顯著差異；

假設3：“人為造假”的首位數、第二位數、前二位數的概率分布與隨機數不存在明顯差異，“人為造假”數據可以視同為隨機數；

假設4：造假者編造的虛假會計數字具有某些統計學上的特征或固有的書寫習慣與偏好。

（三）測試結果

1.首位數測試

表3、表4分別給出了“人為造假”樣本數據與隨機數樣本數據的首位數概率分布值以及與奔福德定律的比較。

由表3可見，“人為造假”樣本數據的首位數概率分布與奔福德定律理論值存在顯著的差異。從相關系數來看，6組“人為造假”的樣本數據均與奔福德定律理論值呈弱正相關關系，其相關系數在0.96184—0.34686之間，其平均值的相關系數為0.92752。此項測試支持假設1。

由表4可見，6組隨機數的首位數概率分布均與奔福德定律理論值呈負相關，其平均相關序數為-0.48321。序數1—9在6組隨機樣本數據的首位數上分布的概率均是圍繞0.1111（即九分之一）上下波動，這樣的概率分布是符合隨機數的統計學特征的。此項測試支持假設2。

圖1和圖2直觀地描述了“人為造假”與隨機數樣本數據首位數概率分布以及與奔福德定律理論值比較的情況。

由圖1可以看出，“人為造假”的數據存在試圖讓1—9在首位數上均衡出現的趨勢，但是相對隨機數而言，其首位數分布概率遠達不到均衡分布的程度；6組人為造假數據中的首位數“1”出現的概率最高，平均值為0.1946，但是仍達不到奔福德定律理論值的水平；“7”“8”“9”在首位數上出現的概率要高于奔福德定律理論值，且低于隨機數的分布值。由此可以推測：造假者在編造虛假會計數字時，會不自覺地在首位數上多用一些“1”，而且會使以“7”“8”“9”開頭的所謂大數字出現得多一些，這應該是造假者在蓄意編造虛假會計數字過程中不自覺顯露出來的思維慣式。此項測試支持假設4。

表5列出了6組“人為造假”與6組隨機數樣本數據的首位數概率分布平均值之間的比較。

表5表明，“人為造假”樣本數據與隨機數樣本數據首位數的概率分布均值存在顯著差異，兩者之間的相關系數為-0.53181，因此不能將“人為造假”數據與隨機數視為等同。此項測試不支持假設3。

2.第2位數測試

表6、表7、圖3、圖4分別給出了“人為造假”樣本數據與隨機數樣本數據的第二位數概率分布值以及與奔福德定律的測試結果比較。

由表6可知，就第二位數而言，6組人為造假的樣本數據與奔福德定律理論值同樣呈弱的正相關關系，其平均相關系數僅為0.5570。此項測試支持假設1。

由表7可見，6組隨機數樣本數據與奔福德定律理論值相比同樣呈弱的正相關或負的相關關系，平均相關系數為0.4046。其顯著特征為序數0—9在第二位數上分布概率在0.10±0.0175的范圍內上下波動。此項測試支持假設2。

圖3顯示，“人為造假”數據在第二位數上與奔福德定律理論值差異最大的是“0”。在6組樣本數據中，“0”在第二位數上出現的最高頻率為0.5254，最低頻率為0.1777，平均頻率為0.3392，均比理論值高。由此可以推測：造假者會不自覺地在第二位數上多用“0”。此項測試結果支持假設4。

表8列出了“人為造假”樣本數據與隨機數樣本數據在第二位數上概率分布均值的比較。表8表明，“人為造假”樣本數據與隨機數樣本數據在第二位數的概率分布均值存在顯著差異，兩者之間的相關系數為0.0833，因此不能將“人為造假”數據等同于隨機數。此項測試不支持假設3。

3.前二位數據測試

表9和圖5分別列出了6組“人為造假”樣本數據與隨機數樣本數據的前二位數概率分布情況。

由表9和圖5可見（限于篇幅，圖表中數據有刪節）：人為造假樣本數據的前二位數概率分布與奔福德定律的理論值呈弱的正相關關系，6組樣本數據中，相關系數最大值為0.5693，最小值為0.2535，平均相關系數為0.6320。此項測試為假設1的成立提供了證據支持。

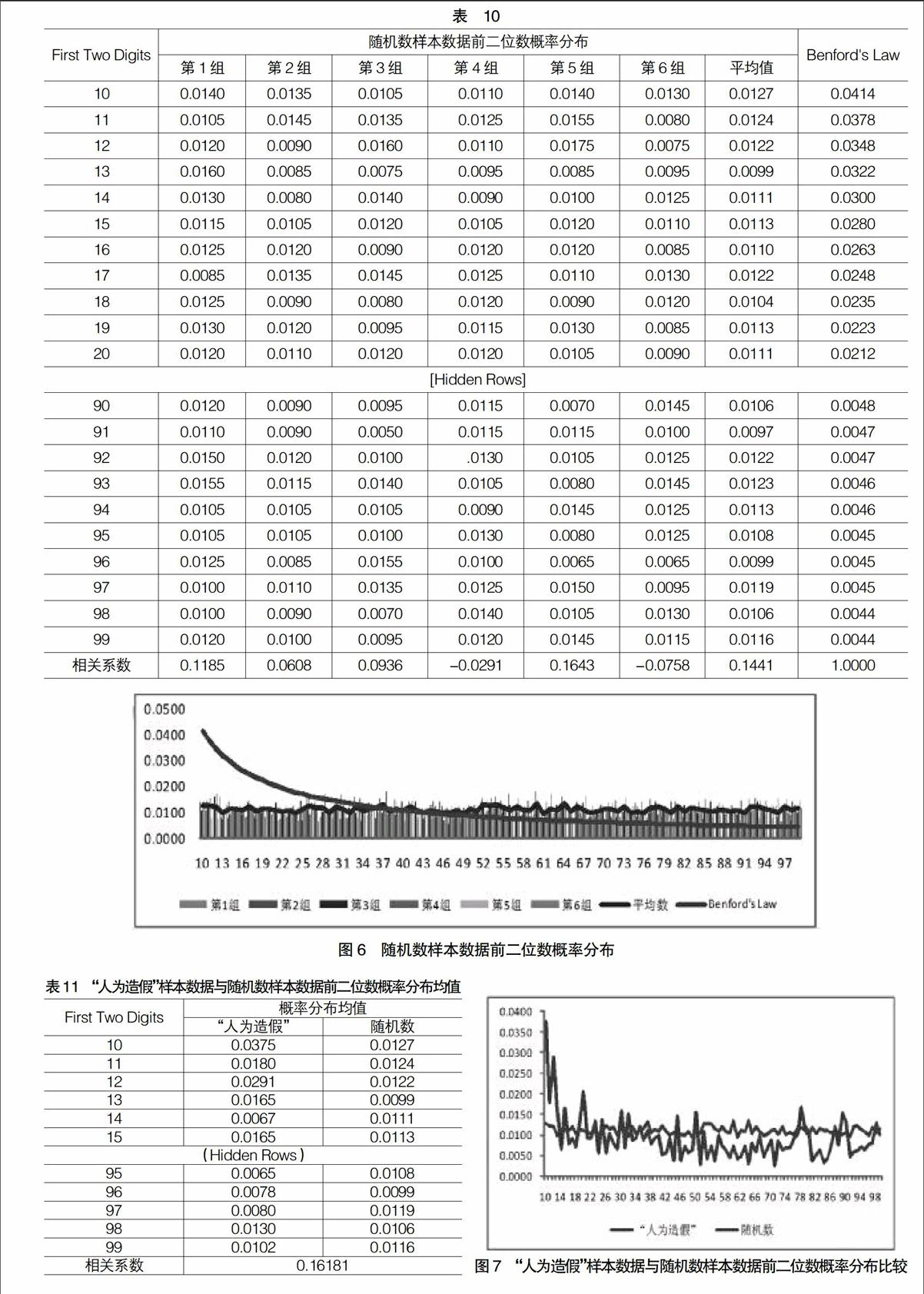
由表10和圖6發現（限于篇幅，圖表中數據有刪節）：隨機數樣本數據前二位數的概率分布與奔福德定律的理論值存在弱的正相關關系，6組樣本數據中，相關系數最大值為0.1185，最小值為-0.0758，平均相關系數為0.1441。其前二位數分布的特征為序數10—99均在范圍為0.01±0.08上下波動。此項測試為假設2的成立提供了證據支持。

表11和圖7列出了“人為造假”樣本數據與隨機數樣本數據在前二位數上概率分布均值的比較。

由表11和圖7可知，“人為造假”樣本數據與隨機數樣本數據在前二位數的概率分布均值存在顯著差異，兩者之間的相關系數為0.1618，鑒于此，不能將“人為造假”數據等同于隨機數。此項測試不支持假設3。

由圖8可以觀察到：“人為造假”樣本數據的前二位數在71—98之間出現高于奔福德定律理論值的三個峰值，而且在10—25之間出現高于隨機數均值且低于奔福德定律理論值的情況。由此可以推測：造假者在編造虛假會計數據時，有在10—25和71—98的區間上選擇前二位數字的傾向。此項測試結果支持假設4。

綜合上述對“人為造假”與“隨機數”的測試分析結果可以得出以下結論：

第一，“人為造假”樣本數據不論是首位數、第二位數還是前二位數的概率分布均與奔福德定律的理論值均存在顯著差異，假設1在本次測試中得到證實。由此可以推論：只要是人為編造的數據，其首位數、第二位數和前三位數的概率分布很難出現與奔福德定律理論值一致的情況。

第二，“隨機數”樣本數據在首位數、第二位數、前二位數上的概率分布值與奔福德定律理論值同樣存在顯著差異，其顯著的特征在于首位數、第二位數和前二位數的概率分別圍繞均值0.1111、0.1000和0.0100波動。假設2在本項測試中得到證據支持。

第三，“人為造假”樣本數據不論是首位數、第二位數，還是前二位數的概率分布均與隨機數樣本數據的相應概率分布值存在顯著差異，假設3在本次測試中沒有得到證明。鑒于此，不能簡單地將人為編造的數據認同為隨機數。

第四，舞弊者在編造虛假會計數字時存在某種共同的選擇取向或固有的選擇習慣，比如，他們會在首位數上多選擇些“1”“7”“8”“9”，在第二位數上多用些“0”等。假設4在此次測試中得到支持，但并不充分。造假者編造虛假會計數字時對序數在不同數位上的選擇取向有待深入研究。

此項測試結果很好地說明了奔福德定律在對“人為造假”數據識別的有效性，為我們利用奔福德定律偵測財務舞弊提供了重要的理論支持。

三、運用奔福德定律進行舞弊審計的啟示與建議

通過對奔福德定律的深入研究與測試分析，可以得到如下啟示：

第一，奔福德定律在舞弊審計領域的運用實際上是分析性復核方法在現代信息技術環境下的發展與有益的補充。傳統的分析性復核方法是從財務數據的內在勾稽關系與邏輯上的合理性角度出發來發現會計錯弊的。而奔福德定律的運用則是借助于現代計算技術從統計學的角度檢測數字在不同數位上的概率分布規律，進而發現會計錯弊的一種新型數值分析方法。奔福德定律在舞弊審計領域的運用豐富了舞弊審計的技術手段，加大了財務造假的難度，提高了舞弊審計工作的效率，豐富與發展了分析性復核方法體系。

第二，運用奔福德定律進行舞弊審計需要特別注意以下方面的局限性：（1）并不是所有的數據類型都適合奔福德定律，運用奔福德定律時要特別注意其限定性條件。（2）檢測的樣本數據與奔福德定律不相符并不說明一定存在舞弊，要注意排除樣本數偏少、存在特定授權交易等情況。此外，樣本數據與奔福德定律不相符只是存在財務舞弊的必要條件，只能說明存在舞弊的跡象或征兆，如果要證實舞弊的確存在，還需“順藤摸瓜”“按圖索驥”才能找到有效的證據。（3）檢測的樣本數據與奔福德定律相符并不說明一定不存在舞弊，尤其是在大樣本數據的情況下，發生次數不多的舞弊數據會被淹沒在大樣本數據的“汪洋大海”之中而無法顯現出來。此時，審計人員應該結合運用分層分析的方法將大樣本“化整為零”。分層測試可以分很多種類，可以按樣本的明細賬戶進行分層，可以針對不同的供貨商、購貨商進行分層，也可以根據不同購貨地區、銷售地區進行分層，還可以根據不同的季度甚至不同月份進行分層。

第三，運用奔福德定律進行舞弊審計還有一個重要的前提：造假者不知曉奔福德定律。在造假者不知曉奔福德定律的情況下，他們對財務數據的編造一般會存在這樣的規律：（1）會不自覺地多選擇一些以“1”為首位數的數字，但是首位數“1”的使用率達不到奔福德定律的理論值；（2）會有意識地多選擇一些以“6”“7”“8”“9”開頭的所謂大數字，特別是我國的造假者會偏愛“6”“8”“9”等吉祥數字；（3）會在第二位數上多用“0”。需要引起注意的是隨著奔福德定律數值分析技術的廣泛應用，對它了解的人會越來越多，造假者會注意到這一規律并會在造假時加以考慮。奔福德定律識別舞弊的有效性會隨著人們對其知曉程度的提高而下降。

第四，可以將奔福德定律及其有關的數值分析工具視為“財務舞弊檢驗器”。利用奔福德定律，可以檢測多種類型的財務舞弊，比如，在我國的證券市場中，對上市公司首次發行股票以及隨后的增發、配股、ST（特別處理）與退市等都有嚴格的限制條件，很多企業會操控財務數據使之迎合政策界限的要求。借助于奔福德定律進行數值分析可以幫助我們透視數字背后隱藏的秘密，評價企業財務數據的質量，同時也可以給政府有關部門提供制定政策的科學依據。為此，建議我國有關部門研究推廣奔福德定律的理論及其數值分析技術，將其納入我國的審計理論與方法體系，進一步豐富我國在現代信息技術環境下應對高智能財務舞弊與經濟犯罪的偵測手段。

第五，在舞弊審計中運用奔福德定律會涉及大量的統計分析工作，如果沒有現代計算機技術的廣泛運用，是不可能完成此項任務的。為解決這一現實問題，國外已經有人開發了專門的應用軟件。許多國外公司開發的計算機輔助審計工具都將奔福德定律作為一個單獨的模塊嵌入其中，比如：ActiveDate for Excel、ACL、IDEA等，大大提高了工作效率。建議我國有關軟件開發機構借鑒國外的相關經驗，盡快開發出具有自主知識產權的奔福德定律應用軟件工具。

結 論

1.人為造假的樣本數據和完全隨機數樣本數據的首位數、第二位數、前二位數上的概率分布值與奔福德定律理論值存在顯著差異；人為造假樣本數據不論是首位數還是第二位數與前二位數的概率分布均與隨機數存在顯著差異，不能將人為編造的數據認同為隨機數。

2.舞弊者在編造虛假會計數字時，對序數在不同數位上的選擇存在某種共同的選擇取向，研究并掌握造假者的數字選擇取向對于識別財務舞弊有重要的意義。該方面的研究尚屬空白，有待進一步發掘。

3.奔福德定律在識別“人為造假”數據方面具有明顯作用，但在實際運用時要注意適用數據的條件和局限性。●

【參考文獻】

[1] AICPA.Statement on Auditing Standards No. 99， Consideration of Fraud in a Financial Statement Audit [A].2002.

[2] WALLACE W. Assessing the quality of data used for benchmarking and decision-making[J].The Journal of Government Financial Management，2002，51（3）：16-21.

[3] GORDON B M，COLIN O B. Using Benfords Law for Fraud Detection[J].Internal Auditing，2004，19（1）：4-9.

[4] CINDY D，WILLIAM H，CARL P. The Effective Use of Benfords Law to Assist in Detecting Fraud in Accounting Data[J]. Journal of Forensic Accounting， 2004（5）：1524-1586.

[5] NIGRINI M J. I've Got Your Number[J]. Journal of Accountancy，1999，187（5）.

[6] NIGRINI M J. Digital Analysis using Benfords Law： Tests and Statistics for auditor[J]. EDPACS，2001，28（9）：1-2.

[7] DRAKE P D，NIGRINI M J. Computer assisted analytical procedures using Benfords Law[J]. Journal of Accounting Education，2000，18（2）：127-146.

[8] 張蘇彤，奔福德定律：一種舞弊審計的數值分析方法[J].中國注冊會計師，2005（11）：70-72.

[9] 張蘇彤，康智慧.信息時代舞弊審計新工具——奔福德定律及其來自中國上市公司的實證測試[J].審計研究，2007（3）：81-87.

[10] 王福勝，李勛，孫遜.奔福德定律及其在審計中的應用研究[J].財會通訊（綜合版），2007（3）：13-16.

[11] 朱文明，王昊，陳偉.基于Benford 法則的舞弊檢測方法研究[J].數理統計與管理，2007，26（1）：41-46.

[12] 許存興，張芙蓉.上市公司資產負債表造假實證分析——基于奔福德定律的研究[J].內蒙古財經學院學報，2009（3）：65-69.

[13] 許存興，張芙蓉.上市公司財務舞弊實證分析[J].天津商業大學學報，2010（3）：51-54.

[14] ROGER S P. On the distribution of the first significant digits[J]. Annals of Mathematical Statistics， 1961，32（4）：1223-1230.

[15] NIGRINI M J. Taxpayer compliance application of Benfords law[J]. Journal of the American Taxation Association，1996，18（1）.

[16] NIGRINI M J，MITTERMAIER L I. The Use of Benford's Law as an Aid in Analytical Procedures[J]. Auditing：A Journal of Practice & Theory，1997，16（2）：52-67.

[17] BASSAM H. Assessing Data Authenticity with Benford's Law[J].Information Systems Control Journal，2002（6）：41.

[18] RAIMI R A. The first digit problem[J]. American Mathematical Monthly，1976，83（7）：521-538.