應用自適應混沌差分進化算法評定圓柱度誤差*

車林仙，易　建，何　兵，黃勇剛

(1. 重慶工程職業技術學院 機械工程學院，重慶　402260；2. 制造裝備機構設計與控制重慶市重點實驗室(重慶工商大學)，重慶　400067；3. 瀘州職業技術學院 機械工程系，四川 瀘州　646005)

應用自適應混沌差分進化算法評定圓柱度誤差*

車林仙1, 2，易建3，何兵3，黃勇剛2

(1. 重慶工程職業技術學院 機械工程學院，重慶402260；2. 制造裝備機構設計與控制重慶市重點實驗室(重慶工商大學)，重慶400067；3. 瀘州職業技術學院 機械工程系，四川 瀘州646005)

摘要：根據評定誤差的最小包容區域準則，應用坐標變換法建立評定圓柱度誤差的4變量無約束優化模型。由于差分進化(Differential evolution, DE)算法具有概念簡單和收斂速度快的優點，文中利用一種改進DE算法——自適應混沌DE(Adaptive chaotic DE, ACDE)算法求解評定圓柱度誤差的無約束優化問題。通過2個基準函數優化問題的對比測試，驗證改進算法的有效性。最后，給出2個圓柱度誤差評定實例。結果表明，ACDE算法的計算效率優于遺傳算法和蜂群優化算法，可靠性和穩健性優于6種對比智能算法。誤差評定模型和求解方法適用于形位誤差測量儀器及三坐標測量機。

關鍵詞：圓柱度誤差；誤差評定；無約束優化；差分進化算法；混沌逃逸

0引言

圓柱面是各類機械零部件中應用最廣泛的規則幾何要素之一，其形狀誤差對機械產品的質量和壽命有很大影響，因此圓柱度誤差測量與評定在機械制造業(尤其是精密制造)中具有重要理論和實踐意義。

圓柱度誤差的常用評定方法有最小二乘法(LSC)和最小區域法(MZC)[1]。LSC的實質是尋找被測圓柱面輪廓對應的理想圓柱面，使各測量點到該理想圓柱面的徑向距離之平方和取最小值。因其評定原理存在缺陷，故該法很難求得精確圓柱度誤差。MZC的實質是尋找兩理想同軸圓柱面，使其包容各測量點，且兩半徑之差取最小值。該法符合ISO1101定義的圓柱度評定方法。多年來，許多學者致力于MZC圓柱度誤差評定模型與算法研究。如，李濟順等[2]將坐標變換法與網格搜索技術結合，再用于MZC誤差評定。

由于MZC圓柱度誤差評定系非線性優化問題，其全局最優解較難獲得，而智能算法是求解優化問題的一類有效方法，因此應用現代智能算法確定圓柱度誤差是計量技術領域的研究熱點之一。貝廣霞等[3]應用遺傳算法(Genetic algorithm,GA)求解MZC圓柱度誤差評定問題，Wen等[4]應用粒子群優化(Particle swarm optimization,PSO)算法求解該問題，羅鈞等[5]應用蜂群優化(Bee colony optimization,BCO)算法求解該問題；Zhang等[6]則提出一種PSO與差分進化(Differential evolution,DE)混合算法，再用于誤差評定優化問題求解。

DE算法是一種簡單高效的群體智能算法，已在數值和工程優化領域獲得廣泛應用[7]。王東霞等[8]應用DE算法評定平面度誤差。車林仙等[9-11]應用改進DE算法求并聯機器人機構位置正解，其實質是求無約束優化問題。本文探索應用DE算法求解MZC誤差評定中的無約束優化問題。

以圓柱度誤差評定為研究對象，在給出最優包容圓筒定義和MZC圓柱度誤差評定原理的基礎上，應用坐標變換法建立確定圓柱度誤差的無約束優化模型，再應用一種改進DE算法——自適應混沌DE(Adaptive chaotic DE,ACDE)算法[9]求解該問題。最后，給出2個誤差評定實例。計算結果表明，ACDE算法的計算效率明顯優于改進GA[3]和具有禁忌策略的BCO算法[5]，可靠性和穩健性優于對比算法。

1圓柱度誤差評定數學模型

應用MZC評定圓柱度誤差，實質是確定包容點集的兩最佳同軸圓柱。為便于敘述，首先給出如下定義。

定義：對于給定的空間點集Sp，作兩同軸圓柱，使兩柱面之間的區域(即圓筒)包容Sp。以兩圓柱半徑之差最小為目標確定的惟一圓筒，稱為最優包容圓筒；其軸線稱為最優軸線。

如圖1所示，設接受圓柱度誤差評定的空間測點集為{Aj,j=1,2,…,J}(J為測點數)，任意點Aj在測量坐標系Oxyz中的坐標為(xj,yj,zj)。根據上述定義和MZC圓柱度誤差評定準則，存在包容該點集的最優包容圓筒。過原點O建立與最優包容圓筒固聯的坐標系OXYZ，且OZ軸平行于最優軸線CC′。由于OZ軸確定之后，OX,OY軸只要滿足右手規則即可，并無特殊要求。為簡便起見，令OY軸位于Oy軸和OZ軸確定的平面內。

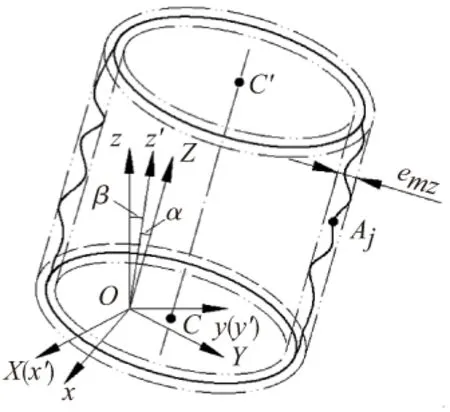
圖1　評定圓柱度誤差的最優包容圓筒

根據運動學原理，可用Y-X-Z型Eluer角表示坐標系Oxyz在坐標系OXYZ中的姿態。因OZ,Oy及OY共面，故可設坐標系OXYZ繞OX軸旋轉α角，得坐標系Ox′y′z′；再繞Oy′軸旋轉β角，得坐標系Oxyz。那么，坐標系Oxyz的姿態可用二維Euler角(α,β)進行降維表示。設測點Aj在坐標系OXYZ中的坐標為(Xj,Yj,Zj)，于是有坐標變換：

(Xj,Yj,Zj)T=Rot(X,α)Rot(y′,β)(xj,yj,zj)T

(j=1,2,…,J)

(1)

式中，Rot(X,α),Rot(y′,β)系旋轉矩陣，分別為

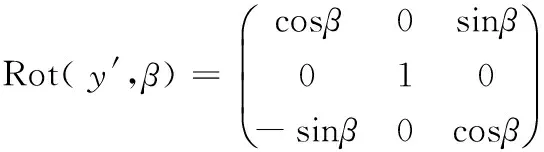
設軸線CC′與平面OXY的交點為C(XC,YC,0)。將所有測點Aj向平面OXY投影，各投影點在平面坐標系OXY中的坐標為(Xj,Yj)。最優包容圓筒則投影為圓環，其厚度即為圓柱度最小誤差emz。該問題的實質是尋找與最優包容圓筒對應的4元參數組(α,β,XC,YC)。若令x=(x1,x2,x3,x4)T=(α,β,XC,YC)T，則確定該最優參數的非線性規劃問題，可轉化為如下無約束優化模型：

(2)

由上式求得最小目標函數值f(x*)，即為MZC圓柱度誤差emz。

常規圓柱度誤差評定方法中(如文獻[3])，通常以理想圓柱軸線的方向余弦參數(其平方和為1)及軸線上一點的3維坐標為待求參數，因此常規方法為6維決策變量。但在方向余弦參數中，只有2個自由變量(本文搜索Euler角α和β)；而理想軸線上有無窮多點，可給定其中1維坐標(本文給定Z=0)，轉為搜索軸線上的唯一點。由此可知，優化模型式(2)無多余變量，變量間不存在約束關系，故式(2)為含4個自由變量的無約束優化問題。

為方便應用，還需求出坐標系Oxyz下的最優軸線CC′單位矢量n0和點C坐標。根據式(1)，可分別得出如下計算式：

n0=(n0x,n0y,n0z)T=[Rot(y′,β)Rot(X,α)]-1(0,0,1)T

(3)

(xC,yC,zC)T=[Rot(y′,β)Rot(X,α)]-1(XC,YC,0)T

(4)

2誤差評定的改進差分進化算法

2.1基本差分進化算法

(5)

(6)

式中，CR(0,1)，為交叉因子；rand()為(0,1)內服從均勻分布的隨機數，對每維分量采樣一次；dr{1,…,4}，為隨機自然數，對每對交叉個體采樣一次，確保試驗個體中至少有一維分量來自變異個體。若分量越界，則在其取值范圍內隨機生成該維分量。

(7)

2.2自適應混沌差分進化算法

ACDE算法詳細流程及收斂性證明參見文獻[9]，以下僅簡述算法改進思路。

(1)分類變異策略

對于目標函數值小于當前代種群平均目標函數值的較優個體，按式(5)生成變異個體；而對于目其余較差個體，則沿目標函數值降低的方向生成變異個體，即將式(5)改進為：

(8)

式中，sgn(·)為符號函數。

(2)混沌逃逸操作

若相鄰兩代種群之間的最優目標函數值滿足

(9)

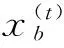
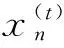
(10)

(3)精英個體保留策略

2.3算法優化性能驗證

應用2個基準函數作為測試問題(均為最小化問題)，以GA,PSO算法,人工蜂群(Artificial bee colony algorithm,ABC)[12]算法,基本DE算法[7](將采用DE/rand/1bin和DE/best/2/bin變異策略的基本算法分別記為DE1和DE2)和帶選擇文檔的自適應DE算法(簡記為JADE[13])等6種算法為對比算法，驗證ACDE算法的有效性。與圓柱度誤差評定問題式(2)類似，這2個函數均為小維數多極值較難優化問題。

Schaffer函數(簡記為SC)：

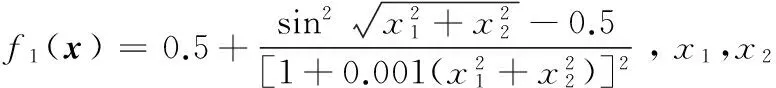
Hartman函數(簡記為HA)：

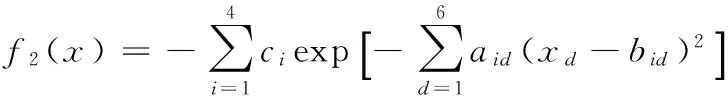
xd[0,1]，d=1,2,…,6。

b=

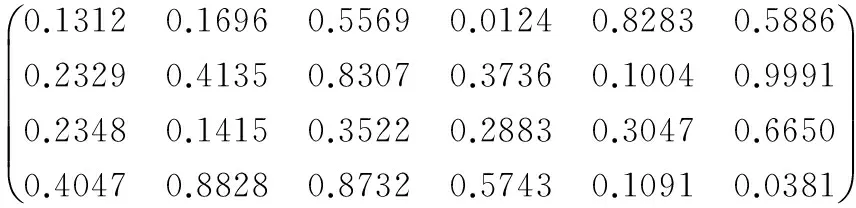
c=(1,1.2,3,3.2)。

為公平起見，7種算法的N及T一致，即均取N=40，T=200。

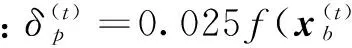
7種算法分別獨立運行50次，優化性能指標統計見表1。表中，fb,fw,fav和σf分別表示最好、最差、平均最優目標函數值和標準差。平均最優目標函數值進化曲線如圖2所示。

要進一步強化基層檢疫申報點建設，科學配置檢疫、日常辦公所需設施設備，合理安排檢疫工作人員，優化檢疫申報點設置，明確檢疫申報點功能，產地檢疫申報點和屠宰檢疫申報點應分開設置，嚴禁混合辦公。要進一步完善檢疫人員準入、退出、考核、獎懲和監督管理制度，加強崗前培訓和在崗人員輪訓，提高檢疫人員業務水平。

表1　7種算法求解測試函數的性能指標比較

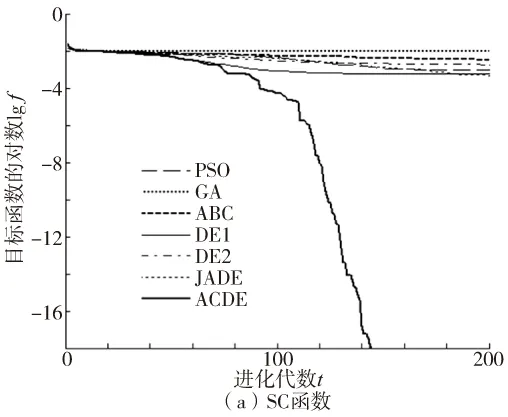
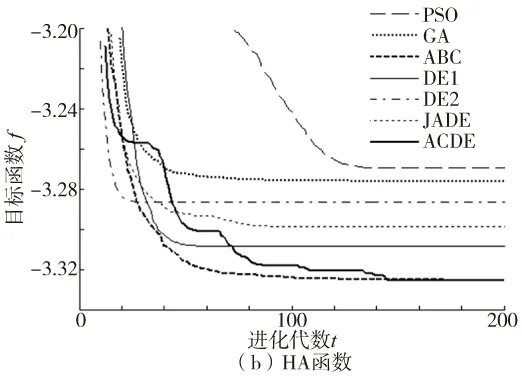
圖2　求解測試函數的平均最優適應度進化曲線

由表1可知，對于2個測試函數，ACDE算法的指標fw,fav和σf均優于對比算法。6種對比算法的fav和σf均偏大(圖2也可印證fav偏大)，表明其優化性能不穩定，有陷入局部最優區域的可能。而ACDE算法的σf很小(求解SC函數時為0)，表明算法陷入局部最優區域后，可通過執行混沌逃逸操作來跳出該區域，使種群繼續搜索全局最優解，因此改進算法具有良好穩健性。

3圓柱度誤差評定實例

3.1誤差評定結果

以下用2個實例(測點坐標見表2和3)來驗證本文模型和算法的有效性。其中，例1數據引自文獻[3,5]，例2數據引自文獻[2]。ACDE算法除T=400外，其余參數設置同SC函數(見第2.3節)。決策矢量取值下限l=(0rad,0rad,-10mm,-10mm)T，上限u=(2πrad,2πrad,10mm,10mm)T。

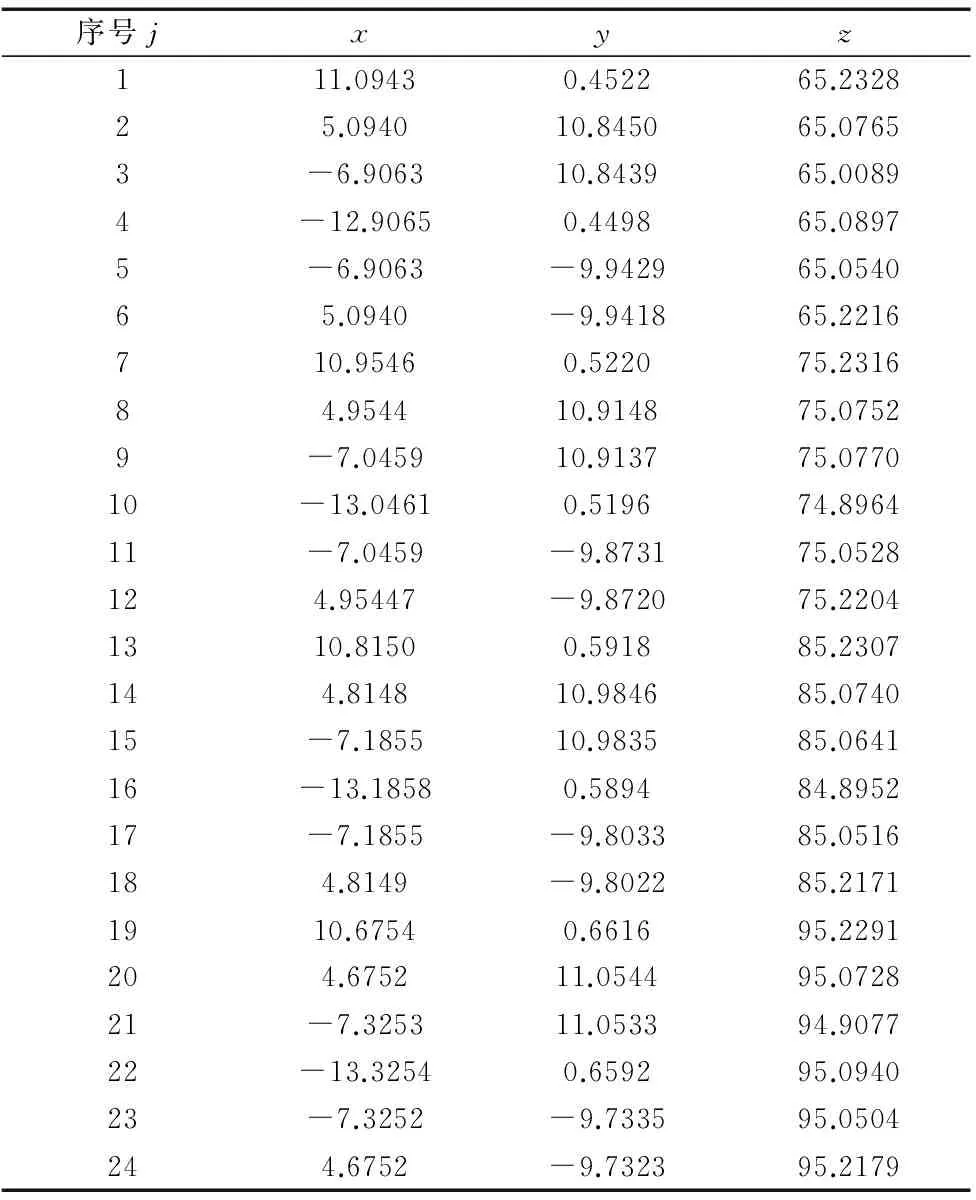
表2　實例1的測點坐標　　mm

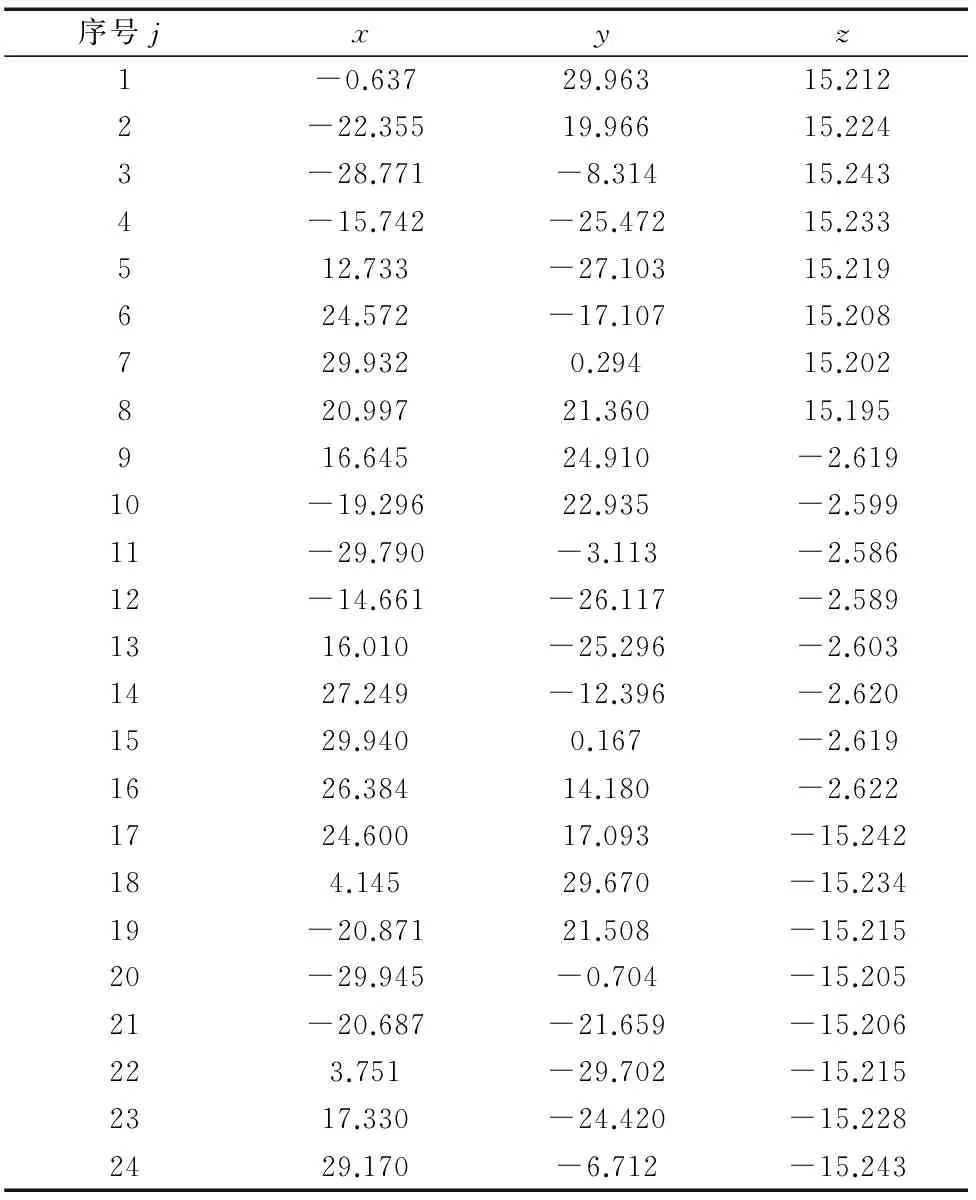
表3　實例2的測點坐標　　mm

應用ACDE算法求得的最優結果見表4。表中，最優軸線CC′單位矢量n0和點C坐標，系最優解分別經式(3)和(4)變換所得。同時，將相關文獻中的最優解也列入表4(其中，點C的坐標是據原文獻位置參數經坐標變換所得)，以便比較。

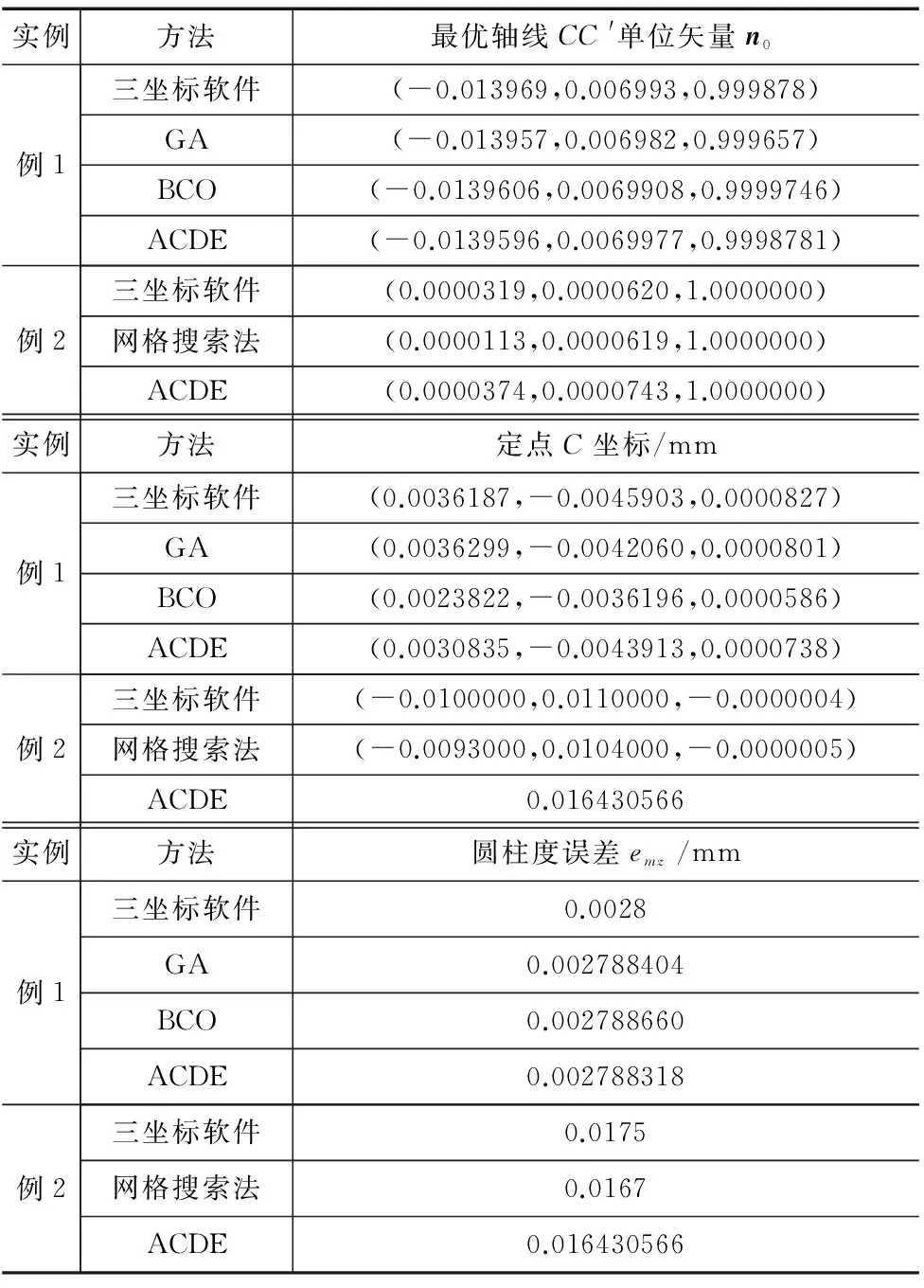
表4　圓柱度誤差評定結果比較

由表4可知，對例1，三坐標測量機軟件[3]、改進GA[3]、具有禁忌策略的BCO算法[5]和ACDE算法確定的最優解接近，但ACDE算法的精度更高。文獻[3]的最大函數評價次數為40000，文獻[5]的函數評價次數為80000；而ACDE算法的基本函數評價次數為16000。ACDE算法獨立運行100次，經統計，該算法因執行混沌逃逸操作而增加的平均函數評價次數為179，相對于基本算法可忽略不計，故該操作幾乎不影響計算效率。因此，本文計算效率明顯高于文獻[3,5]。

對例2，ACDE算法確定的圓柱度誤差較網格搜索算法[2]的最好結果提高約0.27μm。由此可見，ACDE算法的精度高于文獻[2]。

3.27種智能算法對比測試

為驗證ACDE算法求解圓柱度誤差評定問題的有效性，以下仍比較7種算法的性能指標。因篇幅所限，僅給出例1的測試結果。為公平起見，7種算法均取T=400，其余參數設置同SC函數(見第2.3節)。GA和ABC算法均以1/f(x)為適應度。

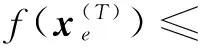
由表5可知，ACDE算法除fb與DE1,DE2和JADE算法相當外，其余指標均好于6種對比算法。GA,PSO和ABC算法的rs為0或1%，表明這3種算法求解例1的全局優化能力差，收斂速度慢(圖3所示平均最優目標函數值進化曲線也可驗證此結論)。DE算法的rs很高，但仍有幾次陷入局部最優區域，導致其fav和σf較大；ACDE算法能全部收斂于全局最優解的鄰域，其fb與fw很接近，σf非常小。由圖3可知，ACDE算法在最差情況下，進化至250代左右即可收斂于全局最優解，表明其斂速快、可靠性高。綜上可知，ACDE算法在計算可靠性和穩健性方面明顯優于6種對比算法。由于ACDE算法具有良好優化性能，故可將文中的誤差評定模型和算法作為關鍵模塊之一，封裝在三坐標測量軟件中，提高評定精度和可靠性。

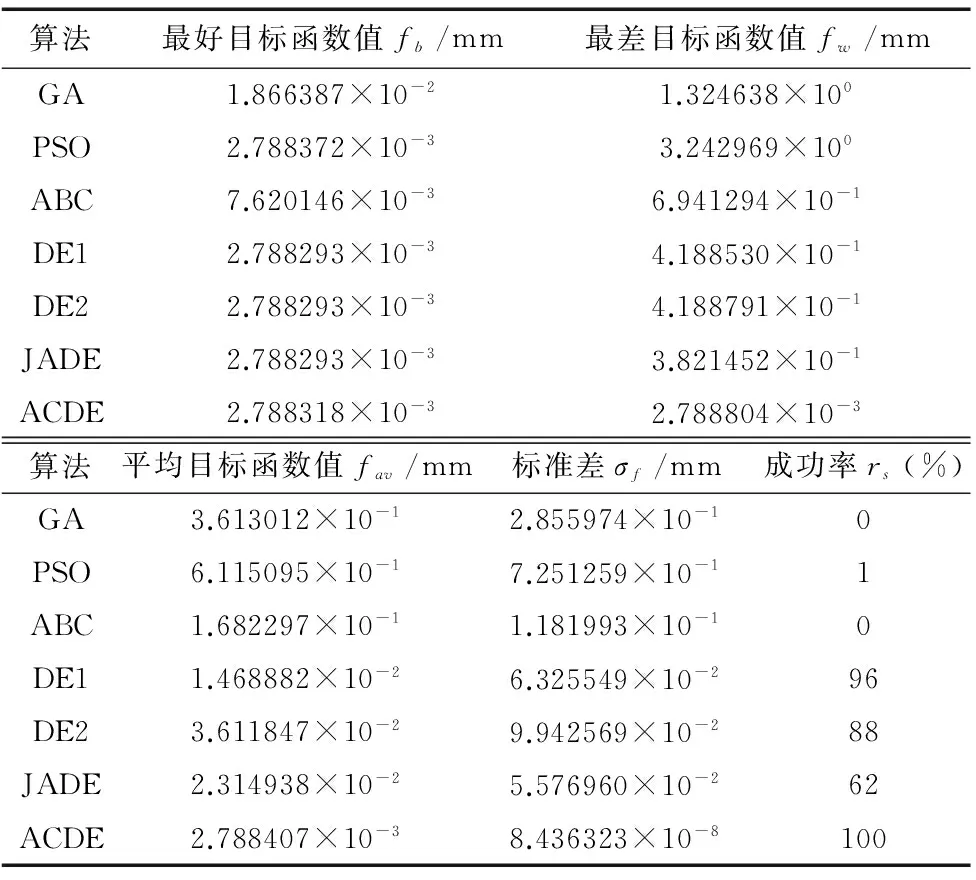
表5　7種算法求解實例1的性能指標比較

圖3　7種算法求解實例1的平均進化曲線比較

4結論

(1)在給出最優包容圓筒定義和MZC圓柱度誤差評定原理的基礎上，應用坐標變換方法，建立確定圓柱度誤差的4變量無約束優化模型。

(2)應用ACDE算法確定圓柱度誤差評定問題的最優解，新算法的最優解與已有文獻結果相當，但計算效率明顯高于對比文獻。本文方法可推廣到其他形位誤差評定問題中。

(3)仿真結果表明：ACDE算法的性能指標fw,fav,σf和rs優于GA,PSO,ABC,基本DE和JADE等6種對比算法，收斂精度和計算可靠性高。

[參考文獻]

[1] 黃祥. 基于最小區域法的圓柱度幾何誤差評定[J]. 組合機床與自動化加工技術, 2013(6): 27-29.

[2] 李濟順, 雷賢卿, 薛玉君, 等. 基于坐標變換的圓柱度誤差評定算法[J]. 中國機械工程, 2009, 20(16): 1983-1986.

[3] 貝廣霞, 樓佩煌, 王曉勇, 等. 基于遺傳算法的圓柱度誤差評定方法[J]. 山東大學學報: 工學版, 2008, 38(2): 33-36, 50.

[4] Wen Xiulan, Huang Jiacai, Sheng Danghong, et al. Conicity and cylindricity error evaluation using particle swarm optimization[J]. Precision Engineering, 2010, 34(2): 338-344.

[5] 羅鈞, 盧嘉江, 陳偉民, 等. 具有禁忌策略的蜂群算法評定圓柱度誤差[J]. 重慶大學學報, 2009, 32(12): 1482- 1485.

[6] Zhang Xiangchao, Jiang Xiangqian, Scott P J. A reliable method of minimum zone evaluation of cylindricity and conicity from coordinate measurement data[J]. Precision Engineering, 2011, 35(3): 484-489.

[7] Das S, Suganthan P N. Differential evolution: A survey of the state-of-the-art[J]. IEEE Transactions on Evolutionary Computation, 2011, 15(1): 4-30.

[8] 王東霞, 溫秀蘭, 汪鳳林. 基于微分進化算法的平面度誤差評定[J]. 組合機床與自動化加工技術, 2013(12): 18-20, 24.

[9] 車林仙. 面向機構分析與設計的差分進化算法研究[D]. 徐州: 中國礦業大學, 2012.

[10] 車林仙, 程志紅, 何兵. 4-PRUR并聯機構及其位置分析的差分進化算法[J]. 機械工程學報, 2010, 46(23): 36-44.

[11] 車林仙, 何兵, 程志紅. 6-CRS并聯機器人機構及其位置分析[J]. 中國機械工程, 2010, 21(14): 1669- 1675.

[12] Karaboga D, Basturk B. A powerful and efficient algorithm for numerical function optimization: Artificial bee colony (ABC) algorithm[J]. Journal of Global Optimization, 2007, 39(3): 459-471.

[13] Zhang Jingqiao, Sanderson A C. JADE: Adaptive differential evolution with optional external archive[J]. IEEE Transactions on Evolutionary Computation, 2009, 13(5): 945- 958.

(編輯趙蓉)

Adaptive Chaotic Differential Evolution Algorithm for Evaluation of the Cylindricity Error

CHE Lin-xian1,2, YI Jian3, HE Bing3, HUANG Yong-gang2

(1. School of Mechanical Engineering, Chongqing Vocational Institute of Engineering, Chongqing 402260, China;2. Chongqing Municipal Key Laboratory of Mechanism Design and Control for Manufacturing Equipment (Chongqing Technology and Business University), Chongqing 400067, China)

Abstract：An unconstrained optimization model with 4 variables is constructed to evaluate cylindricity errors by utilizing the coordinate transformation method according to the minimum zone criteria for evaluating errors. The difference evolution (DE) algorithm is characterized by simple concept and quick convergence. Thus a modified DE algorithm, namely adaptive chaotic DE (ACDE) algorithm, is implemented to solve the unconstrained optimization problem for evaluating cylindricity errors. The modified algorithm is tested against two benchmark examples of function optimization and the results verify its effectiveness. Finally, two real cases for evaluating cylindricity errors are given to test ACDE algorithm, and the experimental results demonstrate that its computational efficiency is superior to that obtained by the genetic algorithm or bee colony optimization, and it outperforms the six compared intelligence algorithms in terms of reliability and robustness. It is suited for evaluation of position measuring instruments and the coordinate measuring machines.

Key words：cylindricity error; error evaluation; unconstrained optimization; differential evolution algorithm; chaotic escape

文章編號：1001-2265(2016)06-0016-05

DOI:10.13462/j.cnki.mmtamt.2016.06.005

收稿日期：2015-07-29；修回日期：2015-08-13

*基金項目：重慶市教育委員會科學技術研究項目(KJ1403201)；四川省教育廳重點科技計劃項目(14ZA0333)

作者簡介：車林仙(1971—)，男，四川瀘州人，重慶工程職業技術學院教授，博士，研究方向為機械優化設計、機構設計和智能信息處理，(E-mail) lx.che@qq.com。

中圖分類號：TH161.13；TG506

文獻標識碼：A