基于五次B樣條的起豎裝置時間最優軌跡規劃*
鄧 飆,張 瀟,龍 勇,郭 楊
(火箭軍工程大學 二系,西安 710025)
基于五次B樣條的起豎裝置時間最優軌跡規劃*
鄧飆,張瀟,龍勇,郭楊
(火箭軍工程大學 二系,西安710025)
摘要:針對含二級電動缸的起豎裝置當前運動軌跡時間不夠優化,且存在不連續沖擊的問題,提出了新的高階樣條軌跡規劃方法。通過對起豎裝置進行建模分析,解得了運動學約束、動力學約束以及邊界條件。使用五次B樣條插值規劃軌跡,引入罰函數處理約束條件,以樣條曲線相鄰控制點的時間間隔為設計變量,利用非支配排序遺傳算法(NSGA-II)對B樣條軌跡進行多目標優化。運算后得到一組Pareto最優解,從中選擇最為平滑且時間最優的解作為最終解。仿真結果表明,相對于多項式插值,樣條插值理論上能實現時間最優;而采用高次樣條插值能得到高階連續的運動軌跡,使起豎過程更加平穩。
關鍵詞:起豎裝置;電動缸;軌跡規劃; B樣條;多目標優化
0引言
二級電動缸相較單級電動缸具有更長的行程,在要求結構緊湊的工業現場設備、農機農具以及大行程軍用雷達、火炮、導彈起落架等起豎裝置中均有廣泛應用[1]。目前,對含二級電動缸的大型起豎裝置起豎過程控制,通常采用分段線性控制的方式及勻加速勻減速方法規劃,該方法雖然能實現理論上的時間最優,但由于加速度不連續,起豎時存在較大沖擊,起豎過程平穩性差,嚴重時影響到系統的安全,所以在設計時往往對加速度的選取比較保守,造成規劃時間過長,不能實現快速起豎。
為解決這一問題,田桂等引入了機器人軌跡規劃中常用的五次多項式規劃方法[2],該方法能解決起豎過程中加速度不連續,平穩性差的問題,但其往往受曲線本身制約,理論上無法實現時間最優。Aribowo、毛征宇等采用三次B樣條曲線插值的方法對運動過程進行軌跡規劃[3-4],利用樣條函數分段處理的特性,綜合運動學與動力學約束,求解出了起豎過程時間最優軌跡,但該軌跡由于加加速度不連續,往往會產生較大且不連續的沖擊,引起機械振動,縮短設備壽命且增大跟蹤控制誤差。
為解決傳統規劃方式平穩性和快速性難以兼顧的問題,選擇五次B樣條插值的方法對負載運動軌跡進行規劃。以樣條曲線相鄰控制點的時間間隔為一組優化目標,提出基于NSGA-II算法求解多目標優化問題的方案。引入罰函數對非顯式非線性不等式約束進行處理,運行算法獲得多個Pareto最優解,從中篩選出自身和各階導數都平滑的運動軌跡集合,再從該集合中選擇總體時間最優的解作為最終解[5]。
1起豎裝置建模分析
1.1起豎裝置的結構與工作原理
大型電動起豎裝置典型結構如圖1。該系統主要由二級電動缸和負載兩部分組成。負載后端與固定裝置鉸接,電動缸的上支耳與負載鉸接,下支耳與固定裝置鉸接,電動缸工作時驅動負載繞定軸轉動,從而實現負載的起豎。從機構學角度分析,該系統做單自由度平面運動,系統的初始位姿、目標位姿和運動路徑均已知,運動時間不確定。

圖1 起豎裝置結構示意圖
1.2起豎裝置運動學模型
建立起豎裝置運動學模型[6]。負載從水平狀態起豎到與水平面成90°角的位置。在運動平面內建立固定坐標系xAy,原點A為回轉中心,C為電動缸上支耳鉸鏈中心,B為電動缸下支耳回轉中心,P為負載重心,r為負載總長,∠CAB=θ0,∠C′AC=θ,∠PAB=β,∠C′AB=ψ,∠BC′A=α。
其中ψ=θ0+θ,則電動缸推桿的伸出位移為:
(1)
推桿的伸出速度為:
(2)
推桿伸出的加速度為:
(3)
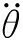
(4)
1.3起豎裝置動力學模型
設整個負載轉動慣量為J,重力為G,電動缸驅動力為F,由系統轉動微分方程得:
(5)
2軌跡優化方案
二級電動缸通過碰撞實現限位。其換級過程是當第一級運行到了行程末端,通過第一級絲杠上的中間塊,將第一級絲杠與第一級推桿固連為一體,共同帶動第二級空心絲杠轉動,使第二級推桿伸出。在進行軌跡規劃時,最理想的狀況就是實現碰撞前的速度為零,為此可將二級電動缸的運動過程分級規劃。因為運動學逆問題比運動學正問題更為簡單,因此先對負載在關節空間的運動軌跡進行規劃,再通過對運動學方程式求取逆解得到二級電動缸的運動軌跡。
2.1基于五次B樣條曲線插值的軌跡規劃
k次B樣條曲線可統一描述為[7]:
(6)
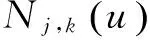
每一段B樣條曲線可表示為:
(7)
式中,i表示第i段B樣條。
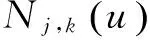
(8)
代入式(7)得到n-1個方程。
又因為在初始位置和末位置處,裝置的運動情況已知
(9)
(10)
(11)
且各階導矢可根據DeBoor遞推公式求出[8]:
(12)
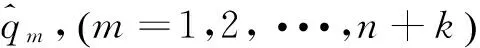
2.2設計變量
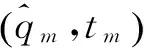
2.3約束條件及其處理
在對每級電動缸的運動軌跡做規劃時,為保證起豎平穩性,負載的起豎軌跡必須是光滑連續的,且滿足以下邊界約束條件[10]。記tf為規劃時間,θ0、θf分別為初始和末態位姿。
(13)
(14)
(15)
且
(16)
將式(1)、(2)、(3)、(5)帶入(16)中,得到了運動軌跡的非顯式非線性約束。
在對約束的處理機制上采用罰函數法,即任何對約束的違反都要在適應度函數中添加懲罰項。在構造適應度函數時,選取罰函數如下:
(17)
3使用NSGA-II算法進行多目標尋優
采用多目標遺傳算法(multi-objectivegeneticalgorithm,MOGA)模擬生物進化過程,處理的是一個種群,能夠在一次優化過程中生成大量的非劣解,因此可以搜索到多目標優化問題的近似Pareto最優解集。許多優化問題往往是對多個相互沖突的目標同時優化,經常需要得到一個解集而不是一個優化解。就全體適應度函數而言,這些解之間是無法比較優劣的。特點如下:無法在改進任何適應度函數的同時不削弱至少一個其他適應度函數。這種解稱作非支配解(non-dominatedsolution)或Pareto最優解(Paretooptimalsolution)。
定義Pareto支配關系如下:對于m個目標分量的最小化多目標向量:
(18)
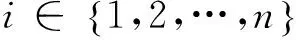
在整個解空間S中都不被其他解支配的所有解得集合P,稱為Pareto最優集(Pareto前沿)。NSGA-II采用快速非支配排序機制,驅使搜索過程收斂到Pareto最優前沿,降低了算法的復雜度;定義擁擠度和擁擠度比較算子,保證了Pareto最優解的多樣性;同時引入精英策略,擴大采樣空間。所謂擁擠距離是指Pareto最優解集中個體的密集程度,表示Pareto解集中個體的分布狀況,擁擠距離越大,說明個體分布越均勻.算法具有O(MN2)的復雜性(其中M為優化目標的個數,N為種群規模),求得的Pareto最優前沿具有良好的分布性。
3.1種群初始化

3.2適應度函數值的計算
根據式(6)計算出每一段B樣條軌跡,并帶入到非顯式約束條件中檢驗,在對約束的處理機制上采用罰函數法,即任何對約束的違反都要在適應度函數中添加懲罰項。文中適應度函數的選取如式(17)所示。依據適應度函數值可求出每代種群個體間的支配關系。
3.3快速非支配排序
在選擇運算之前,根據支配關系計算個體的Pareto秩,以獲取其非劣水平(表征該個體對其他個體的支配能力)。假定個體xi在g代是種群中有pi個個體支配于它,則:
(19)
按非劣水平對每一代個體進行分層[11]。
3.4虛擬適應度
為保持個體多樣性,NSGA-II算法提出了虛擬適應度的概念。計算個體擁擠距離id,圖2中目標空間第i點的擁擠距離等于它在同一等級相鄰的點i-1和i+1組成的矩形2個邊長之和。這一方法可自動調整小生境(niche),使計算結果在目標空間比較均勻地散布,具有較好的魯棒性。
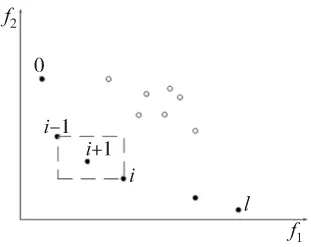
圖2 局部擁擠距離示意圖
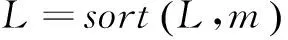
(20)
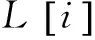
3.5選擇運算

3.6交叉與變異
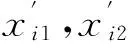
(21)
其中,r為在[0,1]之間產生的隨機數。
仍然選取父代個體x1,針對其中符合約束條件的子目標采用非一致方式[12]變異,從而實現局部尋優。
3.7精英策略
精英策略是遺傳算法以概率1收斂的必要條件。采用的方法如圖3所示。采用精英策略能保留父代中的優良個體直接進入子代。
3.8選擇最終解
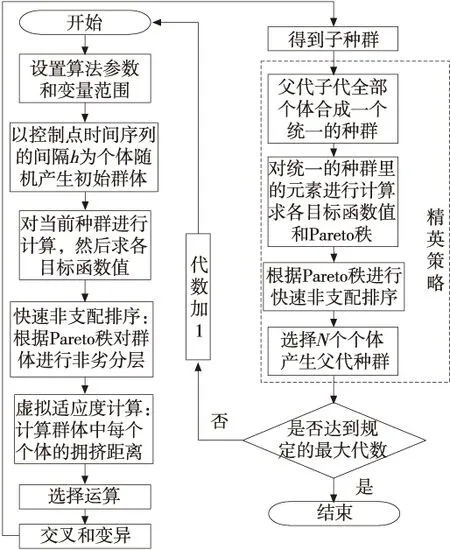
圖3 NSGA-II算法用于B樣條軌跡多目標優化的流程圖
4仿真算例

此外在算例中NSGA-II的參數設置如下:種群規模100,迭代次數為100,交叉率為0.9,變異率為0.1。
經仿真計算,得到一級缸和二級缸的最優起豎時間分別為38.624s和29.837s。經運動學反解后得到了二級電動缸位移、速度、加速度和加加速度(沖擊)與時間的關系,如圖4、圖5所示。
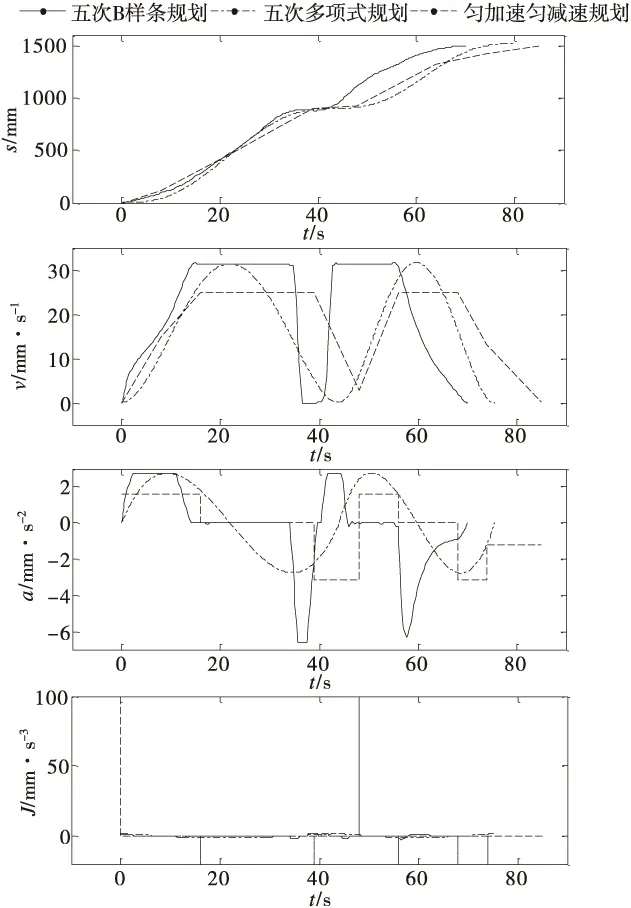
圖4 二級電動缸經規劃后運動情況
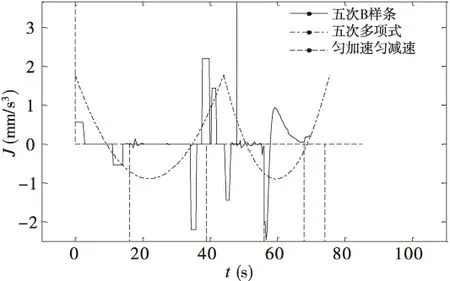
圖5 負載沖擊曲線放大圖
可見,基于五次B樣條的加速度具有C2連續的平滑特性,而基于三次樣條的軌跡加速度雖然也連續,但存在加速度變化劇烈的拐點,在這些拐點所處的時刻,加加速度不連續,這導致電動缸產生軸向振動、擴大跟蹤誤差。
5結論
仿真結果表明:
(1)采用分級規劃策略得到的軌跡,能避免換級碰撞的發生,使沖擊連續平滑,保證了起豎過程的平穩性。
(2)基于五次B樣條插值的時間最優分級軌跡規劃方法,在滿足約束條件的同時,相對多項式規劃方法,五次B樣條插值法能夠實現起豎過程的時間最優;相對傳統勻加速勻減速線性規劃和低階樣條規劃的方法,經五次B樣條插值得到的電動缸運動軌跡具有速度、加速度、脈動連續的特點。
(3)使用NSGA-II算法對五次B樣條插值點時間間隔進行多目標尋優,在適應度函數中引入罰函數處理非顯式非線性約束,相對傳統多目標搜索算法,NSGA-II算法采用精英策略使收斂速度更快;應用快速非支配排序方法使搜索結果分布更均勻,增大了搜索范圍、加強了全局搜索能力。
(4)采用五次B樣條插值的軌跡規劃方法,雖然增加了計算量,但由于起豎過程一般是重復作業,因此軌跡規劃與優化只需進行一次,且起豎過程是離線進行的,對算法的實時性無特殊要求,因此以增加離線計算量為代價獲得性能更優的運動軌跡是一種理想的方案。
該方法對同類的電動起豎裝置軌跡規劃具有一定借鑒意義,也可以應用到工業機械臂領域。
[參考文獻]
[1] 許兵宗, 盧博友. 二級電動缸的設計與研究[D].西安:西北農林大學,2010.
[2] 田桂,謝建,陳永寧. 大型導彈起豎過程最優時間軌跡規劃研究[J]. 計算機仿真, 2012,29(1):41-44.
[3] Wisnu Aribowo, Kazuhiko Terashima. Cubic Spine Trajectory Planning and Vibration Suppression of Semiconductor Wafer Transfer Robot Arm[J]. Automation Technology, 2014,8(2):265 - 274.
[4] 毛征宇,劉中堅. 一種三次均勻B樣條曲線的軌跡規劃方法[J].中國機械工程,2010,21(21):2569-2572,2577.
[5] Hiroshi R. Yamasaki, Urara Nakamura. Temporal Optimality of a Via-Posture on Trajectory during Sit-to-Stand and Back-to-Sit Movements[J]. Biomedical Science and Engineering, 2014, 7:387 -396.
[6] 田桂,謝建,陳永寧,等. 含多級液壓缸的大型液壓舉升系統時間最優軌跡規劃[J]. 機床與液壓,2012,40(3):50-53.
[7] P M 普倫特普. 樣條函數與變分方法[M]. 上海:上海科學技術出版社,1980.
[8] 王會方,朱世強,吳文祥. 基于INSGA_算法的機械手多目標軌跡規劃[J].浙江大學學報(工學版),2012,46(4):622-628.
[9] 余陽,林明,林永才. 基于混合遺傳算法的工業機器人最優軌跡規劃[J]. 計算機工程與設計, 2012,33(4):1575-1580.
[10] 李小霞,汪木蘭,劉坤. 基于五次B樣條的機械手關節空間平滑軌跡規劃[J].組合加床與自動化加工技術, 2012(8):39-42.
[11] 馮士剛,艾芊. 帶精英策略的快速非支配排序遺傳算法在多目標無功優化中的應用[J]. 電工技術學報, 2007,22(12):146-151.
[12] 陳丹, 方康玲. 基于遺傳算法B樣條曲線優化在機器人軌跡規劃中應用[D].武漢:武漢科技大學,2007.
(編輯趙蓉)
Time Optimal Trajectory Planning Based on Five Orders B-spline for Erection Equipment
DENG Biao, ZHANG Xiao, LONG Yong, GUO Yang
(The Second Department,Rocket Force University of Engineering,Xi′ an 710025,China)
Abstract:A new trajectory planning method based on spline interpolation was proposed to solve the problem that the unoptimizable time consumption and discontinuous impact exist in the current trajectory for erection equipment containing the two-stage electric cylinder. Actuating constrains and boundary conditions are obtained through the analysis of kinetic and dynamic models for erection equipment. The five order B-spline interpolation algorithm was adopted for trajectory planning, and penalty function was introduced to process constrains. An NSGA-II algorithm was used to conduct multi-objective optimization for B-spline trajectory while the intervals between each control points of splines were taken as the designed variations. The calculation result was a Pareto optimal solution aggregate, from which the optimal solution is chosen for being the smoothest and the quickest set of intervals. The simulation results show that spline interpolation could achieve optimal time consumption theoretically while the polynomial couldn′t. And high order spline interpolation led to high order continuous trajectories, which makes the erection process more stable.
Key words:erection equipment; electric cylinder; trajectory planning; B-spline; multi-objective optimization
文章編號:1001-2265(2016)06-0021-05
DOI:10.13462/j.cnki.mmtamt.2016.06.006
收稿日期:2015-06-19
*基金項目:國家自然科學基金資助(61304239)
作者簡介:鄧飆(1969—),男,湖北恩施人,火箭軍工程大學教授,碩士研究生導師,博士,研究方向為機電控制,(E-mail)zx82854616@163.com。
中圖分類號:TH112;TG506
文獻標識碼:A

