基于C語言的復合形法的優化設計
摘 要:優化設計是在計算機廣泛應用的基礎上發展起來的一項設計技術,目的是在給定的技術條件下獲得最優設計方案、保證產品具有優良的性能。基于C語言可以很好實現優化設計的算法過程,使解決實際的優化問題變的簡易。
關鍵詞:C語言,復合形法,優化設計
中圖分類號:TH122 文獻標識碼:A
優化設計是在計算機廣泛應用的基礎上發展起來的一項設計技術,目的是在給定的技術條件下獲得最優設計方案、保證產品具有優良的性能[ 4 ]。它首先將設計問題按照規定的格式建立數學模型,并選擇合適的優化算法,選擇或編制計算機程序,然后通過計算機自動獲得最優設計方案。
機械優化設計問題和一般工程實際優化問題絕大多數屬于約束非線性規劃問題,目前對約束最優化問題的解法很多,如復合形法、可行方向法、消元法、懲罰函數法等[ 2 ]。本文根據約束最優化方法中的復合形法提出一種利用C語言程序求解最優解的方法。
一、復合形法基本原理[ 2 ]
復合形法的基本思路是在n維空間的可行域中選取K個設計點(通常取n+1<=K<=2n)作為初始復合形(多面體)的頂點。然后比較復合形各頂點目標函數值的大小,其中目標函數值最大的點為壞點,以壞點之外其余各點的中心為映射中心,尋找壞點的映射點。以映射點替換壞點與原復合形除壞點之外其余各點構成K個頂點的新的復合形。如此反復迭代計算,在可行域中不斷以目標函數值低的代替目標函數值最大的壞點從而構成新的復合形,使復合形不斷向最優點移動和收縮,直到收縮到復合形的各頂點與其形心非常接近、滿足迭代精度ε要求時為止。最后輸出復合形各頂點中的目標函數值最小的頂點作為近似最優點。
現以二維不等式約束優化問題來作進一步說明。其數學模型為:min f(X),X∈D R(2) ,D:g1(X)>=0,g2(X)>=0,a1<=x1<=b1 ,a2<=x2<=b1
在可行域內先選定X(1),X(2),X(3),X(4) 四個點(這里取K=2n=2*2=4)作為初始復合形的頂點,計算這四個點的目標函數值,并作比較,得出壞點X(H)和好點X(L):
X(H):f(X(H))=max{f(X(j)) (j=1,2,……,K)} (1-1)
X(L):f(X(L)))=min{f(X(j)))(j=1,2,……,K)} (1-2)
如果X(4)為好點,點X(1)為壞點,即X(4) →X(L),X(1) →X(H)。以X(2),X(3),X(4)三點的中心,尋找壞點X(H)的映射點X(R):
X(R)= X(C)+α(X(C) -X(H)) (1-3)
式中,α為映射系數,一般α>=1,通常去α=1.3。然后計算映射點X(R)處目標函數f(X(R))與目標函數值f(X(R))相比是否下降,并同時檢查X(R)是否在可行域內。如果下降性、可行性這兩方面都得到滿足,則以X(R)點替換X(H)點,由X(R)與X(2),X(3),X(4)共四個點構成一個新復合形。這個復合形肯定優于原復合形;如果上述兩個條件不能同時滿足,則可將映射系數縮半,即0.5α→α,仍按式(1-3)迭代,重新取得新的影映射點X(R),使其同時滿足下降性、可行性條件。有時甚至要經過多次縮減映射系數才能使回縮的映射點X(R)最后滿足這兩個條件。這時以回縮成功的映射點X(R)和X(2),X(3),X(4)構成新復合形。構成新復合形就完成了一輪迭代。以后再按上述方法進行迭代搜索,不斷地使復合形向著目標函數減小的方向移動和收縮,直到逼近最優解。
二、C語言的概述和作用
C語言是國際上廣泛流行的計算機高級語言。它既有高級語言的特點,又有匯編語言的特點。它適合作為系統描述語言,既可以用來編寫系統軟件,也可以作為應用程序設計語言,編寫不依賴計算機硬件的應用程序[ 3 ]。
下面應用C語言程序利用復合形法求解二元函數minF(X)=x12+x22-x1x2-10x1-4x2+60的最優解,已知D:g1(X)=x1>=0,g2(X)=x2>=0, g3(X)=6-x1>=0,g4(X)=8-x2>=0,取:x1∈[0,6],x2∈[0,8],k=4,迭代精度ε=0.001。
三、C語言程序及功能說明如下
#include/*調用頭文件*/
#include
{printf("This munber is not fit,please input again\n");
i--;
}
}
F[1]=M(x[1][1],x[1][2]);
F[2]=M(x[2][1],x[2][2]);
F[3]=M(x[3][1],x[3][2]);
F[4]=M(x[4][1],x[4][2]);
FH=max(F[4],max(F[3],max(F[1],F[2])));/*尋找壞點*/
FL=min(F[4],min(F[3],min(F[1],F[2])));/*尋找好點*/
loop:for(l=1;l<=4;l++)
if(F[l]==FH)/*判斷第幾個點是壞點*/
{m=l;
switch(m)
{ case 1:{ XX[1]=x[1][1];XX[2]=x[1][2];
x[1][1]=x[2][1];
x[2][1]=x[3][1];
x[3][1]=x[4][1];
x[1][2]=x[2][2];
x[2][2]=x[3][2];
x[3][2]=x[4][2];break;}
case 2:{ XX[1]=x[2][1];XX[2]=x[2][2];
x[1][1]=x[1][1];
x[2][1]=x[3][1];
x[3][1]=x[4][1];
x[1][2]=x[1][2];
x[2][2]=x[3][2];
x[3][2]=x[4][2];break;}
case 3:{ XX[1]=x[3][1];XX[2]=x[3][2];
x[1][1]=x[1][1];
x[2][1]=x[2][1];
x[3][1]=x[4][1];
x[1][2]=x[1][2];
x[2][2]=x[2][2];
x[3][2]=x[4][2];break;}
case 4:{ XX[1]=x[4][1];XX[2]=x[4][2];
x[1][1]=x[1][1];
x[2][1]=x[2][1];
x[3][1]=x[3][1];
x[1][2]=x[1][2];
x[2][2]=x[2][2];
x[3][2]=x[3][2];break;}
}
}
xC1=ZH1(x[1][1],x[2][1],x[3][1]);/*計算映射中心*/
xC2=ZH1(x[1][2],x[2][2],x[3][2]);
a=1.3;/*映射中心系數*/
xR1=xC1+a*(xC1-XX[1]);/*計算映射點*/
xR2=xC2+a*(xC2-XX[2]);
loop2:if(xR1>6||xR1<0||xR2>8||xR2<0)/*判斷映射點是否在可行域內*/
{ loop3:
a=a/2.0;
xR1=xC1+a*(xC1-XX[1]);
xR2=xC2+a*(xC2-XX[2]);
goto loop2;
}
if(M(xR1,xR2){x[4][1]=xR1;
x[4][2]=xR2;}
else goto loop3;
F[1]=M(x[1][1],x[1][2]);
F[2]=M(x[2][1],x[2][2]);
F[3]=M(x[3][1],x[3][2]);
F[4]=M(x[4][1],x[4][2]);
FH=max(F[4],max(F[3],max(F[1],F[2])));
FL=min(F[4],min(F[3],min(F[1],F[2])));
Ff=((1.0/K)*((F[1]-FL)*(F[1]-FL)+(F[2]-FL)*(F[2]-FL)+(F[3]-FL)*(F[3]-FL)+(F[4]-FL)*(F[4]-FL)));
FF=sqrt(Ff);
if(FF>e) goto loop;/*判斷迭代精度是否達到終止條件*/
else
{ for(i=1;i<=4;i++)
if(FL==F[i])
n=i;
printf("The last four point is\n");/*輸出最后一次迭代的4個頂點 及目標函數值*/
printf("x1=%f,%f\nx2=%f,%f\nx3=%f,%f\nx4=%f,%f\n",x[1][1],x[1][2],x[2][1],x[2][2],x[3][1],x[3][2],x[4][1],x[4][2]);
printf("F1=%f\nF2=%f\nF3=%f\nF4=%f\nFH=%f\nFL=%f\nFF=%f\n",F[1],F[2],F[3],F[4],FH,FL,FF);
printf("The perfect answer is\n");
printf("X=%f,%f\n",x[n][1],x[n][2]);/*輸出最優解*/
printf("Fx=%f\n",FL);
}
}
float M(float a,float b)/*定義目標函數*/
{
float F;
F=a*a+b*b-a*b-10*a-4*b+60;
return(F);
}
float max(float x,float y)/*定義取最大函數*/
{
return(x>y? x:y);
}
float min(float j,float k)/*定義取最小函數*/
{
return(j>k? k:j);
}
float ZH1(float x11,float x21,float x31)/*定義取中心點函數*/
{
float Xr1=(x11+x21+x31)/3;
return(Xr1);
}
float ZH2(float x12,float x22,float x32)
{
float Xr2=(x12+x22+x32)/3;
return(Xr2);
}
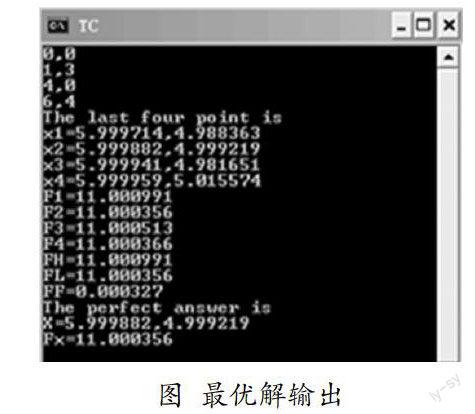
輸入四個點(0,0)、(1,3)、(4,0)、(6,4),輸出最優解如圖所示。
四、結論
通過以上實例可以看出,基于C語言可以很好實現優化設計的算法過程,其效率高,可靠性好,現在有很多成熟的計算機程序可以選用,使解決實際的優化問題變的簡易。
參考文獻:
[1] 楊義勇.現代機械設計理論與方法[M].北京:清華大學出版社,2014.
[2] 陳秀寧.機械優化設計[M].浙江:浙江大學出版社,2008.
[3] 譚浩強.C程序設計[M].北京:清華大學出版社,2007.
作者簡介:邰園園(1987-),男,江蘇句容人,本科,助理工程師,主要從事機械設計工作。

