以“拋物線”概念引入為例談“問題解決”法的課堂引入策略

蔡小沖

[摘 要] 好的教學效果離不開有效的“課堂引入”. 結合問題解決法，數學概念課的引入可以從“借助直觀，揭示本質”，“分層鋪墊，目標分解”，“聯想類比，促進遷移”這三個視角有效切入.

[關鍵詞] 問題解決；高中數學概念；拋物線

每節課都是從“引入”開始的，引入是學生學習概念的基礎. 如何有效引入，借助于引入提高學生的高中數學學習積極性呢？這是一個值得探究的話題.筆者認為引入概念的環節應該是預設問題和激發學生生成問題的重要環節，我們教師問題的預設應該具有針對性和趣味性，要能夠激活學生的思維，將學生帶到對問題的思考與研究中來，能夠切身感受到引入問題的必要性與科學性，當然引入的方式應該是多元化的，本文以拋物線的概念教學為例就如何引入從不同的視角進行研究，望能有助于課堂教學實踐.

直觀化的引入，揭示概念的本質

高中生的數學思維往往還是以形象思維為主，隨著數學概念的抽象性增強，學生感覺學習數學越來越難. 這時怎么辦？尤其是有些生源較差的學校和班級，如何幫助學生理解抽象的數學概念呢？筆者認為應該注重教學的直觀化處理，或采用實物，或引入直觀的數學模型，借此建立直觀的問題情景，引導學生由表象出發引出比較抽象的數學性質.

例如，拋物線概念的直觀化引入可以進行如下設計：

1. 設計思路

從學生的生活實際來看，我們可以引導學生觀看生活中的拋物線實例（多媒體輔助）：噴泉；跳水運動員高臺跳水；飛機投炸彈等等.但是學生對于“概念”本身的理解是有難度的，為什么？學生面對生活中的這些實例，軌跡是不具體和直觀的，對于實例中給出的軌跡到底是什么？學生無法憑空想象，如何解決？采用直觀模型可以很好地解決.

2. 直觀化導入設計

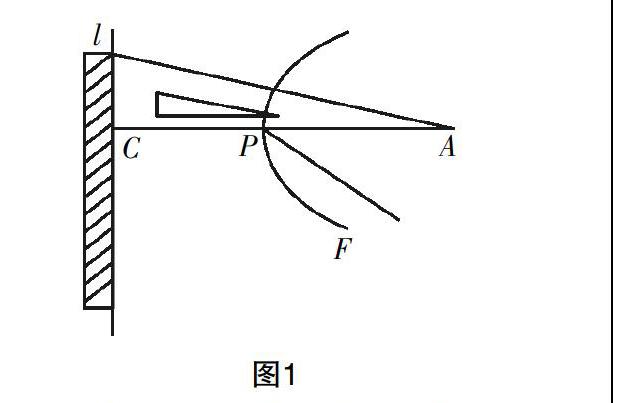
（1）在黑板上畫一直線l，接著將直尺固定于直線l上，如圖1所示；

（2）接著拿一個三角板，將其一條直角邊靠近直尺的邊緣；

（3）取一根細線，并截取細線長度等于AC，將其一端固定于三角板上的A點，另一端固定在黑板的一個點F上；

（4）請一學生走上講臺，用一支鉛筆緊扣細線，并借助于三角板的直角邊AC將細線繃緊讓三角板沿著直尺上下滑動；

（5）觀察滑動過程中鉛筆留下來的曲線形態，分析曲線的特點.

3. 設計意圖

借助于上面直觀化的操作，5個環節的活動化操作，問題自然生成，整個運動軌跡可以是作為P點的運動，學生的思維轉向該點具有怎樣的幾何特征呢？增加了“概念”的可信度，學生通過對直觀化模型的分析，很自然地推出拋物線的定義，同時，筆者發現學生在思考與解決問題的過程中，有部分學生還提出了，如果點F在直線l上會是什么結果呢？通過進一步的思考，概念變得更為精致.

循序漸進地引入，分解學習目標

每節課都有核心概念，這是我們教學的知識目標所在，但是這個目標與學生的學情又往往存在一定的差距，怎么辦？我們在導入的時候如果發生這種情況，筆者認為最佳的辦法就是分解目標，并循序漸進地引入，引導學生拾級而上逐步地接近數學概念的本質.

例如，“拋物線”概念的循序漸進地引入設計如下.

1. 設計思路

考慮到大多數學生的學情，從學生的原有認知來看，他們對于拋物線與二次函數圖象的聯系，以及生活中有關物體拋物線狀的運動軌跡是有一定的認識基礎的.

那么，學生學習該概念存在的問題在哪里？

從初中的教材來看，學生是對拋物線有了一定的了解，但是初中教材對于“概念”更多的是描述性的，對于拋物線的本質特征沒有涉及，初高中教材中對于拋物線的概念差距很大.可以說是幾乎完全不同.怎么辦？采用目標分解的引入方法，可以進行如下的設計.

2. 提出問題

問題1：我們在初中都學過二次函數y=ax2+bx+c（a≠0），還記得它的圖象是什么樣？（拋物線），請你大致地畫出該圖象.

問題2：到下面收集一個學生畫的拋物線并實物投影，然后將拋物線順時針（或逆時針）轉了90°，大家思考一下，這個圖象還是不是拋物線呢？

學生對于開口朝上、朝下、朝左、朝右的拋物線有了一定的認識后，設置具體的活動，深入探索拋物線概念的本質.

3. 活動探究

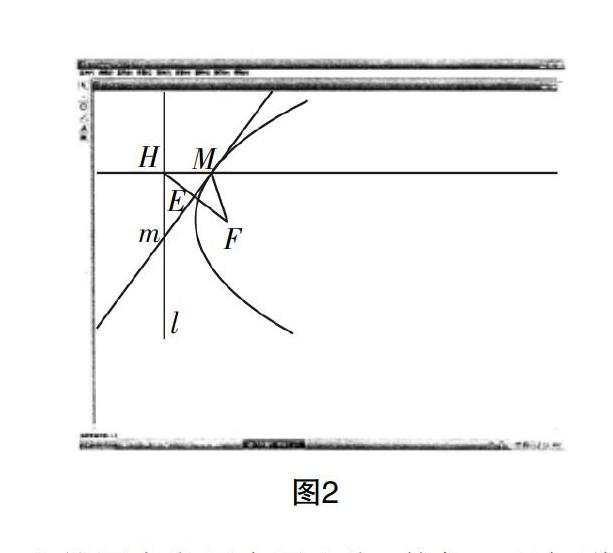
借助于“幾何畫板”進行動態演示，如圖2所示，定點F，直線l為不經過點F的定直線，H點為l上任意一點，現在過點H作MH⊥l，m為線段FH的垂直平分線，與MH交于點M，然后拖動點H，引導學生觀察點M的軌跡，思考點M滿足怎樣的幾何條件.

4. 設計意圖

問題的設計和活動的設計均從學生的原有發展水平出發，他們已經知道y=ax2+bx+c（a≠0）的圖象為拋物線，由此出發找學生潛在的發展水平——“拋物線的定義”. 什么是拋物線？“拋物線是到定點距離等于到定直線的距離的點的軌跡”. 上述設計從學生容易接受的知識出發，結合幾何畫板這一直觀的工具實現了一步步思維和認知的跨越.

聯想類比式導入，構建數學知識體系

學生的知識學習除了在某一個概念上深化外，還可以從其他數學概念的學習過程中將經驗遷移到新概念的學習中來.

例如，拋物線概念的聯想類比引入，可以進行如下設計.

1. 設計思路

從數學知識結構來看，“拋物線”、“橢圓”、“雙曲線”這三個概念存在著千絲萬縷的聯系，我們可以站在統一的視角去思考“曲線的生成”、“曲線的性質”和“應用”等問題，但是實際的情況如何呢？學生解決實際問題的能力并不理想，什么原因導致的呢？筆者認為在概念課教學時，缺乏相互聯系的滲透，為此在教學過程中應該注重類比與聯想.

2. 提出問題

問題1：從學生前面學習的橢圓、雙曲線出發，設置具有啟發、引導性問題，在前面的學習中，我們已經研究了橢圓和雙曲線，知道平面內一個定點與到一條定直線的距離的比是常數e的點的軌跡，回憶一下分別滿足什么條件軌跡為橢圓和雙曲線？（橢圓，01）.

問題2：如果e=1，軌跡又是什么呢？

3. 活動探究

此處的探究與“上文二”中的活動探究一樣，不再贅述.

4. 設計意圖

該種導入方式，在引入概念的階段，從學生已有的知識基礎（橢圓、雙曲線概念及其學習過程）出發，創設了有利于激發學生學習主動性的問題情境，激活內驅力.從問題的設計來看，問題的切入點在于“離心率的關系”，“橢圓”和“雙曲線”的“離心率的關系”學生是熟悉的，那么問題拋出引發認知沖突，即為什么兩個概念中都不涉及e=1的情況呢？如果e=1，軌跡又是什么呢？通過這個問題很自然地完成思維的切換，學習活動自然過渡到對“到定點和定直線距離相等的點的軌跡”的探究. “橢圓”、“雙曲線”、“離心率”等概念是學生的原有發展水平，在討論和交流的過程中，類比到新概念，同時學生的大腦中對于幾種圓錐曲線的聯系也有了初步的印象，為概念的統一和數學知識結構化建立打下基礎.

通過上文的分析，我們可以總結出“問題解決”法的課堂引入的基本原則：第一，我們的導入環節應該注重直觀性原則. 數學概念較為抽象，學生不易理解，所以要充分借助直觀模型，幫助學生更好地理解概念，促進學生對概念的掌握；第二，我們的導入環節也應該注重過程性原則，即不是直接將概念拋給學生，數學概念的形成，是一個逐步完成的過程，并不是一蹴而就的，很多概念的形成，都需要經歷一些必要的過程，因此我們要認識到概念形成的過程性，在導入階段從學生的認知基礎出發設置合理的問題，讓學生通過對問題的思考和活動探究來嘗試著解決問題，逐步接近概念；第三，我們的導入還應該注重數學知識的內在結構性. 數學概念具有嚴謹的邏輯結構，富有層次性. 所以我們要充分認識到這一點，通過合理的方法，選擇恰當的策略，促使學生建立概念網絡，促進概念的理解.