基于K-Medoid聚類算法的GPS坐標轉換研究

王　偉，黃　騰，葛　文，曹曉楨，張浩然

(1.河海大學 地球科學與工程學院，江蘇 南京 210098；2.國家基礎地理信息中心，北京 100830)

?

基于K-Medoid聚類算法的GPS坐標轉換研究

王偉1，黃騰1，葛文1，曹曉楨1，張浩然2

(1.河海大學 地球科學與工程學院，江蘇 南京 210098；2.國家基礎地理信息中心，北京 100830)

摘要：對GPS網約束平差時，GPS控制網的精度與坐標系統轉換控制點的位置選擇有關。通過實驗分析得出，整個網的檢核點與相應的轉換控制點總距離越遠，坐標轉換后網的精度越低。在此基礎上，提出使用K-Medoid聚類算法，通過計算機程序自動尋找用于計算坐標系統轉換參數的最佳控制點，并將文中方法運用于某大橋GPS控制網的控制點選取，通過工程實例驗證了基于K-Medoid聚類方法的GPS坐標系統轉換的可行性。

關鍵詞：K-Medoid算法；GPS網；基線解算；網平差；坐標轉換；精度評價

GPS定位技術[1]的平面精度能達到1～2 mm，甚至能達到亞毫米級。實際工程中，需要對GPS接收機直接獲取的WGS-84坐標進行轉換，得到GPS網點的工程獨立坐標。目前,常用轉換方法的主要技術路線如下：在測區選取2個或2個以上的轉換控制點，聯測高等級的點，利用四參數模型[2]或七個參數模型[3-4]，計算得到GPS網的WGS-84坐標系與地方獨立坐標系之間的轉換參數，再對GPS網進行約束平差，獲取GPS控制網的工程獨立坐標。已有研究表明[5]，在基線質量良好的情況下，若轉換控制點選取不合理，會導致整個網扭曲變形，改變網點誤差的分布規律，從而使相應的方差與協方差模型產生變化，降低GPS網精度。行業相關規范中對轉換控制點的選擇并沒有明確規定，實際工程一般根據經驗來選擇，但是并不能保證選取的轉換控制點是合適的。本文針對上述問題，將機器學習中的K-Medoid算法(K中心點算法)引入到控制點選取中，優化控制點選取方案，從而獲得最佳控制點，提高GPS網的精度。

1K-Medoid聚類算法

聚類是將數據對象分組為多個類或簇，劃分原則是在同一個簇中的對象之間具有較高的相似度，而不同簇中的對象差別較大，每一個類可以通過一些特征來描述。K-Medoid聚類算法[6]選用簇中位置最中心的對象作為代表對象，試圖對n個對象給出k個劃分，代表對象稱為中心點，其他對象被稱為非代表對象。在K-Medoid聚類算法中，可以把過程分為以下2個步驟：

1)建立。尋找k個中心點作為初始的類中心點。

2)交換。對于所有的可能的對象進行分析，找到交換后可使得非代表對象到該對象的歐氏距離和最小的對象，代替原中心點。

2GPS網精度評價

2.1Chi-SquareTest

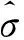
(1)

對母體方差σ2進行假設檢驗的方法，稱為χ2檢驗法。

2.2Tau-test

(2)

檢驗正態母體的數學期望。GPS基線解算中，Tau檢驗一般用來檢驗參與平差的基線是否存在粗差[7]。

2.3QA檢驗

三維無約束平差后計算的基線向量中誤差應滿足預設值。QA檢驗[7]通過，表示基線向量中誤差滿足期望值。

3工程概況

臨海高等級公路灌河大橋總體呈東西走向，橫跨灌河，測區范圍東經119°45′～119°50′，北緯34°23′～34°25′，北部位于連云港市境內，南部位于鹽城市境內，線路總長約7.5 km。測區內地勢平

坦，海拔2 m左右，因灌河南北兩部分測區之間通行極為不便，布設GPS施工期控制網，等級GPS測量主要技術要求見表1。主橋、GH-1標引橋、GH-2標引橋GPS控制網測量點位縮略圖分別見圖1～圖3。

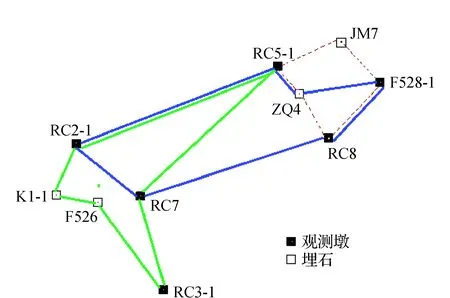
圖1　主橋GPS測量點位略圖

圖2　GH-1標引橋GPS測量點位略圖

圖3　GH-2標引橋GPS測量點位略圖

等級衛星高度角/(°)同時觀測有效衛星數/個平均重復設站數/(次/點)時段長度/min數據采集間隔/sGDOP值三等≥15≥4≥2≥905～15≤6

特大型橋梁的施工期一般在2年以上，施工周期長，控制點使用頻繁。由于該橋梁工程施工區域通常地質條件較差，周圍作業機械較多，控制點不穩定因素較多，易受到破壞，因此，需定期對點位的穩定性進行檢核，并進行修正。若坐標轉換控制點不穩定，則需重新選取轉換控制點。

4基于K-Medoid聚類算法的坐標轉換的精度模擬分析

為了解決網的精度及點位誤差大小與轉換控制點位置的關系問題，利用計算機進行數據模擬，采用控制變量的方法，只研究控制點的偶然誤差對網精度的影響。模擬過程如下：

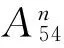
2)灌河大橋三等GPS網要求最弱點點位中誤差≤±5 cm，在測量平差學科中，有如下極限誤差理論：

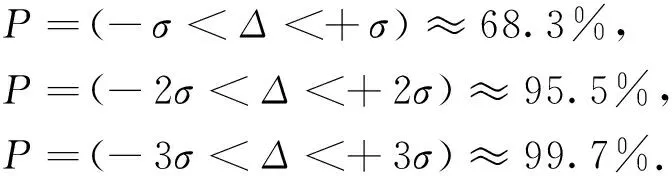
(3)

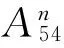
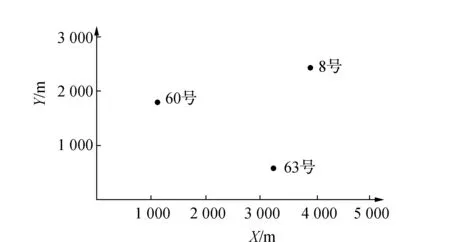
圖4　K-Medoid算法選取的轉換控制點

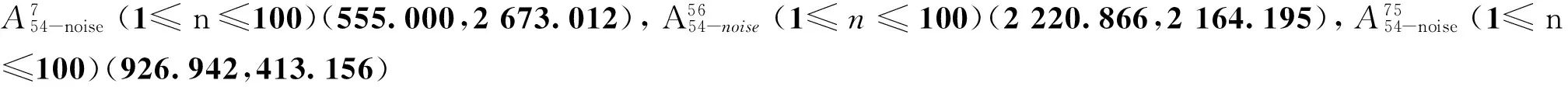
4)按如下公式計算2個不同轉換模型下的點位誤差。得到點位精度對比圖(見圖6)，選取最大點位誤差、最小點位誤差、小于兩倍中誤差比例、大于兩倍中誤差比例作為評價指標，得到精度分析表(見表2)。

圖6　K-Medoid聚類算法與人為選取轉換控制點點位誤差比較

(4)

(5)

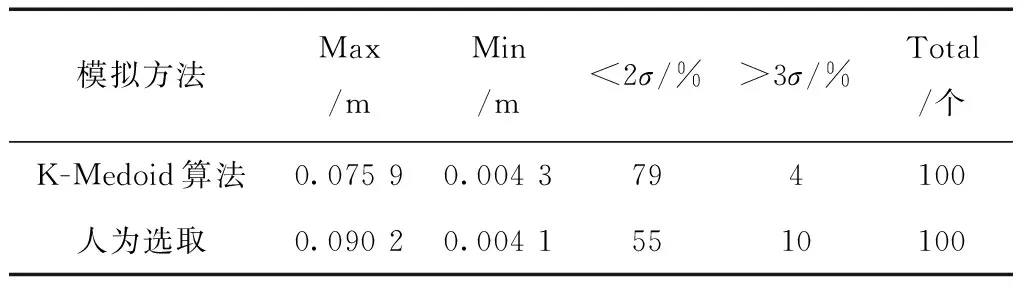
表2　K-Medoid聚類算法與人為選取轉換控制點精度分析

5工程實例分析

5.1GPS數據預處理

5.1.1數據文件預處理

本實驗利用Ashtech solution軟件對基線進行基線處理。由于不同數據處理軟件有各自特定的數據格式，在數據處理前，需將GPS數據觀測文件轉換為RINEX數據格式。

5.1.2基線解算及質量檢核

基線解算過程主要分以下3步：①解算整周未知參數和基線向量浮動解；②將整周未知數固定成整數；③將整周未知數作為已知值，求解基線向量固定解。

基線解算完畢后對基線解算結果進行質量檢核[8]。內容包括同步環檢核、異步環檢核以及復測基線檢核等，保證基線質量合格后，對GPS網進行平差。

5.1.3三維無約束平差

進行網格坐標系(北京54高斯投影后的平面坐標系)下的無約束平差，獲取測區內各GPS控制點的北京54平面坐標。將生成的各控制點的北京54平面坐標以電子表格的形式存檔，作為K-Medoid聚類算法聚類的原始數據。

5.2基于K-Medoid聚類算法的轉換控制點選取

K-Medoid聚類方法的實現借助于MATLAB，按照K-Medoid聚類的思想編寫程序。為了體現實驗方法的科學性，將整個處理過程分為以下2步：

1)三維無約束平差后，分別對各控制點的北京54平面坐標的三維空間坐標和二維平面坐標的聚類，共分成3類。為防止出現局部最優解，選取不同的初始點重復試驗。試驗結果顯示，當重復聚類次數超過20次后，得到的聚類結果唯一；無論選用三維坐標還是二維坐標進行聚類，最終選出的聚類中心一致，依次是JM13、JM2-1、F524，其具體位置如圖7所示，聚類之后各個點的分類情況見圖8。

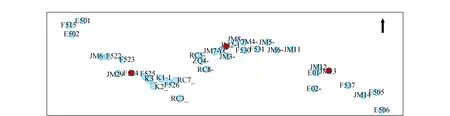
圖7　轉換控制點點位分布圖

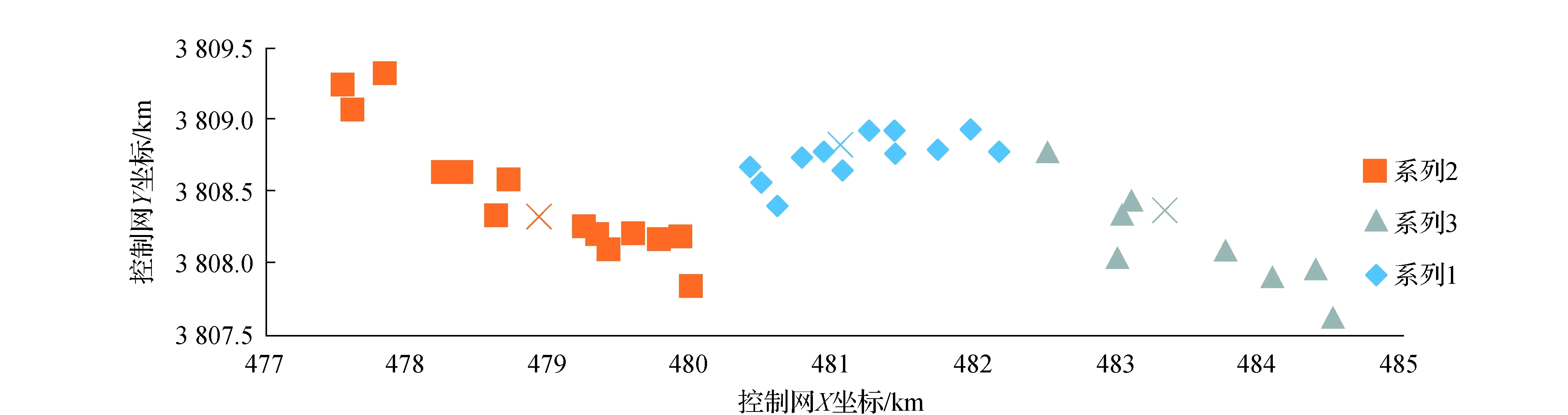
圖8　控制點分類結果，以相同圖例表示同一類控制點

2)選取聚類得到的JM13、JM2-1、F524這3個點作為轉換控制點，對控制網進行約束平差。在網平差結束后，應對網平差結果進行檢驗，網平差的檢驗主要通過改正數、中誤差以及相應的數理統計檢驗結果等項來評價。利用Ashtech solution軟件的“Ashtech Network Adjustment Package”網精度評價模塊提供的各項精度指標，對網精度進行評判，三維約束平差后的各項網精度指標如表3所示。

表3　三維約束平差網精度指標

平差結果顯示，利用K-Medoid聚類算法找出轉換控制點并進行在當地坐標系下約束平差后，該工程實例GPS網精度符合各項限差要求，網的各項精度指標得到保證。

6結論

利用K-Medoid聚類算法，通過計算機程序實現GPS網最佳轉換控制點選取的方法，能夠保證坐標轉換控制點均勻分布于控制網，對測區域形成整體控制，從而能保證GPS網精度。灌河大橋施工期控制網的實例驗證了基于K-Medoid聚類方法的GPS坐標系統轉換的可行性，可為其他工程實例提供參考。

參考文獻：

[1]徐紹全.GPS測量原理及應用[M].武漢：武漢大學出版社，1998.

[2]韋鋮，馬文雙，李明君.工程測量中平面坐標轉換軟件設計及應用[J].測繪工程，2013，22(4):76-79.

[3]田桂娥，宋利杰，尹利文，等.地方坐標系與CGCS2000坐標系轉換方法的研究[J].測繪工程，2014，23(8):66-69.

[4]王解先.七參數轉換中參數之間的相關性[J].大地測量與地球動力學，2007，27 (2):43-46.

[5]陶葉青，楊娟，趙強.控制點因素對GPS坐標系統轉換精度的影響[J].北京測繪，2012(1)：5-7.

[6]KAUFLNAN L，ROUSSEAUW P J.Finding Groups in Data：An Introduction to Cluster Analysis[J].Journal of the American Statistical Association，1990.

[7]武漢大學測繪學院測量平差學科組.誤差理論與測量平差基礎[M].武漢：武漢大學出版社，2003.

[8]王瑞.GPS基線精度分析及控制網的方差分量估計研究[D].南京：河海大學，2005.

[責任編輯：劉文霞]

DOI:10.19349/j.cnki.issn1006-7949.2016.08.006

收稿日期：2015-04-27

作者簡介：王偉(1991-)，男，碩士研究生.

中圖分類號：P228.4

文獻標識碼：A

文章編號：1006-7949(2016)08-0024-05

A study of GPS coordinate transformation theory based on the algorithm of K-Medoid

WANG Wei1，HUANG Teng1，GE Wen1，CAO Xiaozhen1，ZHANG Haoran2

(1.School of Earth Science and Engineering，Hohai University，Nanjing 210098，China；2.National Fundamental Geographic Information Center，Beijing 100830，China)

Abstract：When conducting the constraint adjustment of GPS network，the accuracy of GPS control network is related to the choice in the location of the conversion control points of the coordinate system.Through the experimental analysis，the paper reaches a conclusion：the longer the total distance of the checking points and conversion control points are，the lower precision of the network is.Based on this conclusion，the algorithm of K-Medoid is used to find the best conversion control points and applying this to the GPS network of a certain bridge can prove the feasibility of this method.

Key words：algorithm of K-Medoid；GPS network；baseline processing；network adjustment；transformation of coordinate；evaluation of precision