抗差主成分估計在板塊運動參數解算中的應用
李亞萍,孫付平,朱新慧,丁 赫,陳競男
(1.信息工程大學 導航與空天目標工程學院,河南 鄭州 450000;2.信息工程大學 地理空間信息學院,河南 鄭州 450000)
?
抗差主成分估計在板塊運動參數解算中的應用
李亞萍1,孫付平1,朱新慧1,丁赫1,陳競男2
(1.信息工程大學 導航與空天目標工程學院,河南 鄭州 450000;2.信息工程大學 地理空間信息學院,河南 鄭州 450000)
摘要:為解決在采用空間大地測量數據求解板塊運動歐拉參數過程中可能出現的矩陣病態問題,以及消除粗差對解算結果的影響,利用抗差主成分估計方法,采用IGG3方案的選權迭代方案對北美板塊的2 577個臺站進行檢測,剔除包含粗差的異常站數據,求出歐拉參數最優解,并進行誤差估計,建立北美板塊的運動模型。計算結果表明,剔除異常臺站前后精度有一定的提高,參數結果與其他模型的解算結果具有較強的一致性。
關鍵詞:抗差主成分估計;歐拉參數;誤差估計;北美板塊
在板塊運動機理研究中,通常假定板塊是剛體,而事實上板塊并非嚴格意義上的剛體,板塊內局部地區和邊界地區都存在著形變。因此,在建立板塊運動模型時,必須選擇板塊穩定主體內的臺站,才能完全反映板塊的主體運動。許多研究基于最小二乘求解的,當觀測誤差服從正態分布且觀測方程狀態良好時,采用最小二乘估計具有較好的優越性,但對偏離主體分布的粗差不夠敏感。若觀測臺站所處的環境發生變化,臺站就有可能會出現異常,有粗差的存在。本文嘗試以北美板塊臺站數據為實例利用抗差主成分估計的方法對臺站進行篩選處理,以期剔除異常臺站,選擇更合理的臺站解算歐拉參數的最優解。
1歐拉參數求解原理
通常用歐拉矢量參數反映板塊運動的狀態,根據歐拉定律,板塊運動歐拉矢量Ω與測站地心速度V之間關系
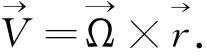
(1)
式中:r為測站地心位置矢量。已知V和r可估計出Ω。地心速度與歐拉矢量的關系式:
(2)

板塊運動主要反映在水平站速度之中,VLBI、SLR、GPS 3種技術確定垂向站速度受到的干擾因素還不能進行規范的建模,直接采用地心站速度V可能會使板塊運動參數估計受到垂向站速度誤差的影響。因此,在實用中常把測站地心速度轉換為站心速度,采用其水平分量來求解板塊運動歐拉矢量Ω。
1)測站地心速度轉換為站心速度:
(3)
將式(2)代入式(3)得到站心坐標速度與歐拉矢量的關系式
(4)
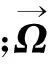
(5)
2)精度評定。速度單位權中誤差σ0
(6)
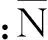
速度協方差矩陣Qvv,
(7)
式中:A′為剔除后的系數矩陣。
(8)
(9)
2抗差主成分估計模型及計算
2.1抗差主成分估計模型
設參數平差的函數模型為

(10)
式中:L為觀測值向量,X為待求參數向量,A為X系數矩陣, Δ為誤差向量。
X的LS估計為
(11)
設N=AΤPA;?1,?2,?3,…,?t為N的t個特征值;λ1,λ2,…,λt所對應標準化特征向量。
為表述方便,假定λ1,λ2,…,λt依次降序排列。
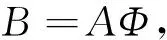
記
(12)
式(10)改寫為
(13)
如果矩陣A呈病態,假定有λl+1,λl+2,…,λt接近于零,并將Λ,Λ1,Λ2記為
(14)
若矩陣A呈病態,則式(12)中的Φ1為前l個標準化非零特征向量組成的矩陣,Φ2為λl+1,λl+2,…,λt對應的標準化特征向量。
則有定義推出主成分估計
(15)
根據抗差M估計原理,可得參數X的抗差估計為
(16)
可推導得到抗差主成分估計
(17)

(18)
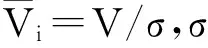
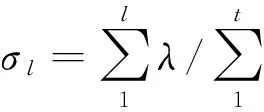
2.2參數計算
建立誤差方程
V=AX+L.
(19)
其中
(20)
整個迭代過程用流程圖1表示。需要指出的是,初步處理的數據,在此次計算中作為原始數據。求解(AΤPA)特征根以及相應的特征向量,并按照第二種方法,嘗試進行主成分個數的確定,進而確定Λ1,且根據實驗精度要求以及以往的經驗值給定值C=0.95,也即通常所說的置信度為95%。

圖1 計算流程
3結果分析
3.1數據說明
本文采用的數據從美國國家大地測量局(NGS)網站下載獲取,包括站點坐標以及速度矢量,為了充分更精確地研究板塊的運動機制,還將布設在SLR、VLBI的臺站數據進行統一處理,納入到板塊運動參數求解中,分布展點見圖2。為避免
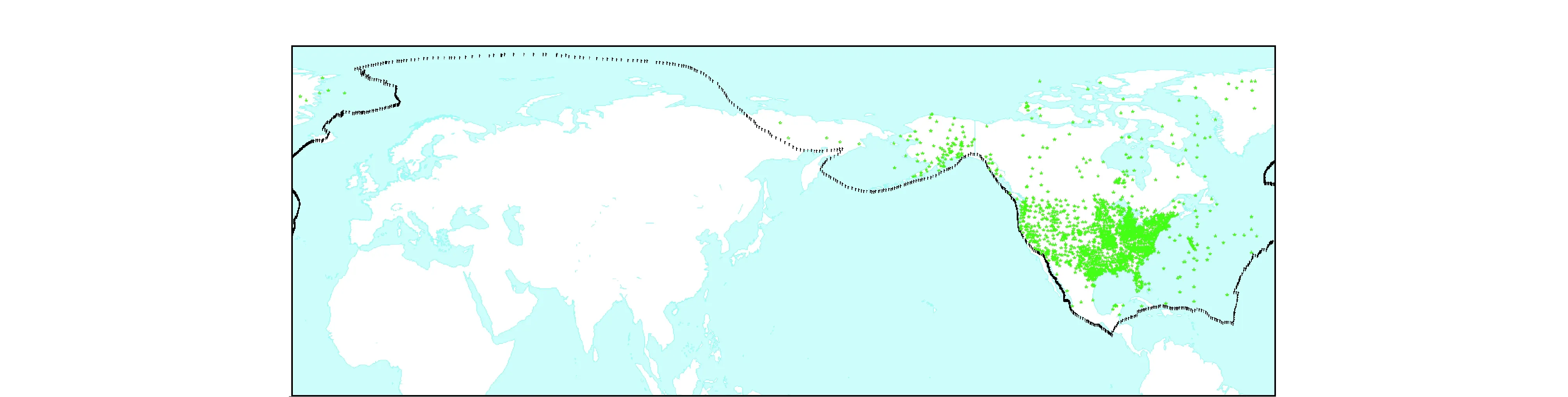
圖2 臺站展點圖
原始數據存在的較明顯的粗差帶來不必要的干擾,先采用文獻[1]中提到的3個原則進行初步篩選。對數據進行歷元統一,統一到歷元2005。經過初步處理,選取2 557個站參與抗差估計計算。
3.2結果分析
從計算過程可知,法方程系數矩陣的條件數N=256,可知存在中等程度病態問題。在迭代過程中經過多次試驗,發現降權中的k1=3.0更為合適,因為在滿足篩選臺站條件下,盡可能多的臺站有利于提高解算精度。水平速度殘差百分比見圖3,剔除異常臺站前后水平速度均方根誤差。歐拉參數及其中誤差分別見表1、表2。
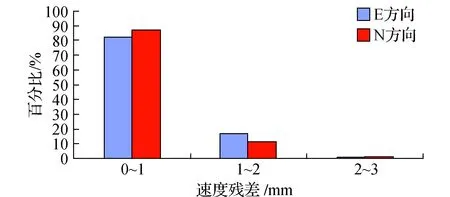
圖3 水平速度殘差百分比
對歐拉參數進行檢驗,選擇其它模型進行比較,結果如表3所示。
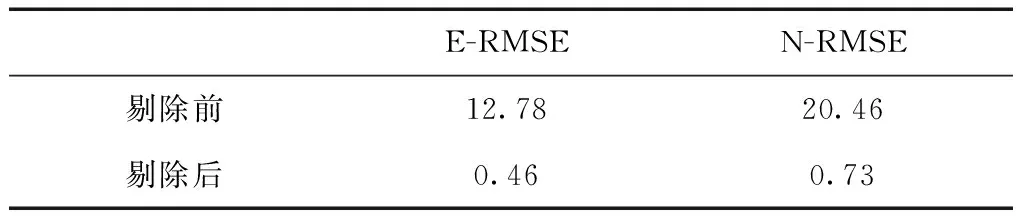
表1 剔除異常臺站前后水平速度均方根誤差(RMSE)

表2 歐拉參數中誤差

表3 幾種模型的比較
注:Ⅰ.NNR-NUVEL1A[10]估計結果;
Ⅱ.朱文耀(2000)ITRF96[11]估計結果;
Ⅲ.柴洪洲 ITRF2005[12]估計結果;
Ⅳ.朱新慧 ITRF2008VEL[13]估計結果;
V.本文嶺估計結果
由表1可知,剔除異常臺站前,臺站的水平方向的速度東向和北向的均方根誤差(E-RMSE 、N-RMSE)分別達到12.78,20.46,而利用抗差模型剔除異常站后,二者分別減小到0.46,0.73,說明剔除異常站后,說明利用抗差主成分模型計算的精度明顯提高。
表2給出了利用抗差方法后求得的歐拉參數的中誤差,結果表明其精度達到10-7量級,說明求解的參數具有較好的精度,可靠性強。
水平速度殘差在一定程度上反映數據的質量,由圖3可知,殘差在1 mm以內的百分比均能達到80%以上,說明數據精度質量很好。由表3可以看出,本文求得的結果與其他學者的結果基本上在同一個量級,但是也有一定的差別,原因是其他學者的研究大多基于地學資料、ITRF系列的研究,采用的數據量相對本文較少,臺站的選擇不同,求解的結果也會有不同。這些結果相差在一定的范圍內,說明板塊的整體運動在一定時期內是相對穩定的。
4結束語
利用抗差主成分估計方法,采用IGG3方案的選權迭代方案對北美板塊的2 577個臺站數據進行檢測,剔除包含粗差的異常站數據,求出歐拉參數的最優解,并進行誤差估計,建立北美板塊的運動模型;計算結果表明,臺站的水平方向的速度東向和北向的均方根誤差明顯降低,殘差在1 mm以內能達到80%以上,說明抗差的效果較好,求解的參數具有較好的精度,可靠性強。不足之處,僅對北美板塊的運動參數進行解算與分析,需利用該方法進行選站,以期解算全球范圍內的板塊參數,進一步利用最優歐拉參數進行理論速度的計算,進而可以與實測速度進行比較,分析各個塊體內部變形情況。
參考文獻:
[1]金雙根.確定板塊運動學模型的臺站選取[J].大地測量與地球動力學,2003,23(3):56-60.
[2]黃立人.用于相對穩定點組判別的QUAD法[J].大地測量與地球動力學,2002,22(2):10-15.
[3]徐克科.利用抗差估計進行剛性板塊異常臺站探測及其運動參數求取[J].大地測量與地球動力學,2014,34(2):95-99.
[4]柴洪洲.最小二乘配置方法確定中國大陸主要塊體運動模型[J].測繪學報,2009,58(1):61-65.
[5]明鋒,柴洪洲.利用半參數模型求解板塊運動參數[J].大地測量與地球動力學,2008,28(3):104-107.
[6]隋立芬,張超.抗差主成分估計及其應用[J].測繪學院學報,1996,13(3):195-199.
[7]楊元喜.抗差估計理論及其在大地測量中的應用[D].北京:中國科學院,1991.
[8]周江文.經典誤差理論與抗差估計[J].測繪學報,1989,18(2),115-120.
[9]黃維彬.近代平差理論及其應用[M].北京:解放軍出版社,1992.
[10] ARGUS D F,GORDON R G.No-Net-Rotation Model of Current Plate Velocities Incorporate Motion Model NUVEL-1[J].Geophys.Res.Lett.,1991,18(11):2039-2042.
[11] 朱文耀.基于ITRF96和ITRF97板塊運動模型[J].天文學報,2000,41(3):312-319.
[12] 柴洪洲.全球板塊運動背景場及ITRF2005VEL的建立[J].測繪科學技術學報,2009,26 (2):79-85.
[13] 朱新慧,孫付平,王刃.運用空間技術建立絕對板塊運動模型[J].武漢大學學報(信息科學版),2012,37(3):282-285.
[14] 張洪文,趙忠海,朱李忠,等.利用GPS基線長度研究南極板塊穩定性[J].測繪與空間地理信息,2015,38(5):18-20.
[責任編輯:李銘娜]
DOI:10.19349/j.cnki.issn1006-7949.2016.08.009
收稿日期:2015-05-11
基金項目:國家自然科學基金資助項目(41374027)
作者簡介:李亞萍(1989-),女,碩士研究生.
中圖分類號:P226.3
文獻標識碼:A
文章編號:1006-7949(2016)08-0038-04
Application of principal components estimate to the calculation of plate motion parameters
LI Yaping1,SUN Fuping1,ZHU Xinhui1,DING He1,CHEN Jingnan2
(1.School of Navigation and Aerospace Engineering,Information Engineering University,Zhengzhou 450000,China;2.School of Geographic Spatial Information,Information Engineering University,Zhengzhou 450000,China)
Abstract:To solve the problem of motion matrix morbid appearing in the process of solving the Euler parameters of plate motion using the space geodetic data,and to eliminate the influence of gross error on the results,this paper detects the 2 577 stations of North American plate by using principal component estimation method with IGG3 iteration scheme.The abnormal station data containing gross error is eliminated.Then the North American plate motion model is established with the optimal solution of Euler parameters and error estimation.The result shows that the accuracy increases to a certain extent before and after excluding abnormal stations and the results have strong consistency with other models.
Key words:principal component estimate;Euler parameter;error estimate;North American plate

