高校課堂教學質量雙權定量分析

劉大江

(唐山學院 土木工程學院，河北 唐山 063000)

?

高校課堂教學質量雙權定量分析

劉大江

(唐山學院 土木工程學院，河北 唐山 063000)

摘要：基于普遍性、規律性和適用性原則，將高校課堂教學質量眾多影響因素進行優化、整合，建立了課堂教學質量評價指標體系。應用熵確定評價指標權重，以未確知測度理論構建綜合評價模型，再輔以AHP法確定課程教學質量綜合評價值。實證表明，運用未確知熵模型進行課堂教學質量評價的適應性與可操作性較強，評價結果真實、客觀。

關鍵詞：教學質量；雙權定量分析；未確知測度；熵

課堂教學始終是我國高校最基本、最關鍵的教學組織形式[1]。當前隨著高等教育規模的日益擴大，高等教育質量成為備受關注的社會熱點，而教師的課堂教學質量是高等教育質量的生動體現和可靠保障。因此，建立科學有效的課堂教學質量評價體系和方法，積極開展科學、客觀、公正的課堂教學質量評價，使之對教學發揮診斷、導向和激勵三大作用[2]，對于優化教學過程、提高教育教學質量具有十分重要的理論和現實意義。

由于課堂教學質量的影響因素繁雜，且呈高度非線性和不確定性關系，數據的收集存在很大的隨機性、未確知性，故難以用傳統的方法來準確評價。目前，許多國內外專家、學者針對課堂教學質量的評價問題進行廣泛深入的研究，提出了許多有價值的定量分析方法，如：專家經驗法[3]、標準分法[4]、層次分析法[5]、模糊綜合評價法[6]、主成分分析法[7]、熵權法[8]和粗糙集法[9]等。客觀而言，上述方法各具特色，各有優劣，對高校課堂教學質量的評價提供了重要的參考和有益的借鑒。本文基于組合研究思想，構建未確知測度熵模型，以信息熵確定評價指標的權重，對課堂教學質量進行評價，并通過實證分析對模型適應性、可操作性和精確度進行驗證，以期獲得更加科學、客觀的評價結果。

一、課堂教學質量評價指標體系

針對高等教育課堂教學的目標與特點，切實貫徹教育部、財政部《關于“十二五”期間實施“高等學校本科教學質量與教學改革工程”的意見》(教高[2011]6號文件)相關精神，遵循普遍性和規律性相結合、目標性和導向性相結合、科學性和實用性相結合的原則[10]，選取教學態度、教學內容、教學方法和手段、教學能力和水平、教學效果等決定課堂教學質量的關鍵因素構建高校教師課堂教學質量評價指標體系[11-13]，如表1所示。

表1　課堂教學質量評價指標體系

二、未確知測度模型

(一)設定空間

(1)設對象空間為論域U={x1，x2，…，xn}，其中xi(1≤i≤n)表示第i個待評測對象；

(2)設論域U的指標空間I={I1，I2，…，Im}，其中Ij(1≤j≤m)表示第j個指標；

(3)設有序評價空間C={C1，C2，…，Cq}，其中Ck表示第k項評價等級(1≤k≤q)，且Ci>Ci+1；

(4)設xij表示對象xi關于指標Ij的觀測值；

(5)設μijk(1≤i≤n，1≤j≤m，1≤k≤q)表示在指標Ij狀態下，評價對象xi與評價等級Ck的接近程度，且同時滿足非負有界性、可加性和歸一性三個條件，稱為未確知測度[14]。

(二)單因素未確知測度

(三)確定指標分類權重

指標分類權重是表示各評價因素對方案分類的影響程度，其合理性直接影響到評價結果的準確性，擬采用信息熵的理論確定指標權重。測度μijk表示指標Ij對xi的分類做出的貢獻，則由μijk所確定的信息熵表達為

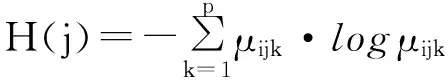
(2)

令

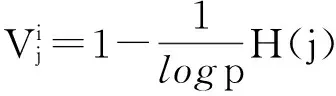
(3)

(4)

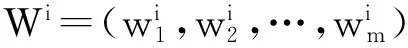
(四)多因素綜合未確知測度

由xi未知測度矩陣與xi各指標分類權重向量結合，構建多因素綜合測度評價矩陣。

μi=Wi·(μijk)m×p=

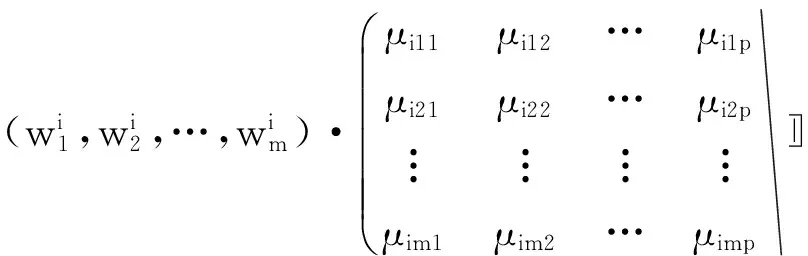
(5)

稱μi=(μi1，μi2，…，μip)為xi的評價向量。

(五)未確知測度評價模型的識別

根據認識率最大和拒識率最低準則，采用置信度識別準則進行未確知測度評價模型的識別。設置信度為λ(λ>0.5)，通常取λ=0.6～0.7，令

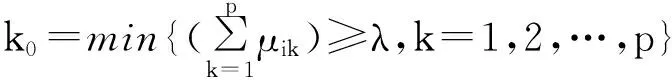
(6)

則判定xi屬于第k0個評價等級Ck0。

(六)綜合評價值計算

為能夠更加客觀地體現評價對象間的優劣排序，利用雙權法計算各評價對象的綜合評價值

S=μ·SiT。

(7)

三、實證分析

唐山市某高校為全面貫徹落實教育部相關文件精神，完善和發展教學質量監控體系，著力提高高等教育教學質量，擬對全校專任教師所承擔各門課程的課堂教學質量進行評測。該高校成立了由教學督導組10名專家、教師所在院(系)2名主管教學的領導以及院(系)內8名相同或相近專業的專職任課教師組成的“課堂教學質量評審委員會”。該委員會與待評課程任課班級所有學生共同構成“課堂教學質量評教系統”，每門課程的最終評價結果由該評價系統的相關組成部分加權評價取得。針對各評測主體所處地位和對評價結果重要程度，結合學校教學實際，“課堂教學質量評審委員會”運用Delphi法和AHP法[15]確定課堂教學質量評教系統中督導組專家、院(系)領導、同專業教師和學生的評價權重R=(0.27，0.13，0.20，0.40)。

“課堂教學質量評審委員會”成員通過隨機聽課、調查問卷、走訪座談等方式廣泛、客觀地收集待評課程的相關信息，確定某課程課堂教學質量的評價空間C={C1，C2，C3，C4，C5}與對應的賦分區間(如表2所示)。

表2　待評課程課堂教學質量評價賦分表

教學督導組專家對教師甲所承擔課程A的課堂教學質量各項指標的評測數據如表3所示。

表3　課程A的課堂教學質量評價指標的評測數據

由公式(1)知，督導組專家對教師甲所承擔課程A的課堂教學質量評價的單指標未知測度矩陣

根據公式(2)-(5)，運用Matlab軟件計算出督導組專家對教師甲所承擔課程A的課堂教學質量各評價指標權重向量為

W=(0.1271，0.0753，0.0401，0.0447，0.0447，0.0330，0.0599，0.0447，0.0565，0.0447，0.0259，0.0528，0.0599，0.0753，0.0599，0.0142，0.0447，0.0330，0.0375，0.0259)。

則督導組專家對教師甲所承擔課程A的課堂教學質量評價的空間向量為

μ1=W1·(μ1jk)m×k=(0.1524，0.2218，0.3143，0.2349，0.0766)。

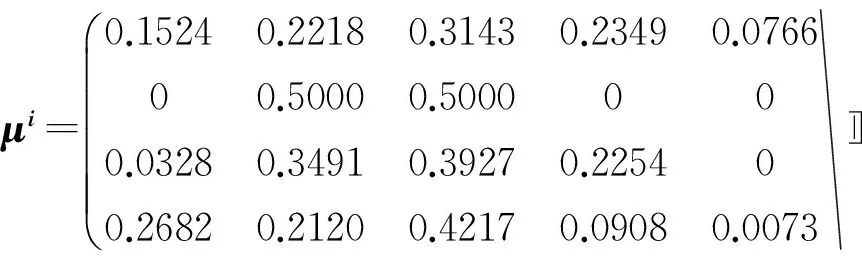
則對教師甲所承擔課程A的課堂教學質量評價的加權綜合空間向量為

μ=R·μi=(0.1550，0.2795，0.3972，0.1448，0.0235)。

取λ=0.65時，據公式(6)知：k0=0.1550+0.2795+0.3972=0.8317>λ，則k=3，即教師甲所承擔課程A的課堂教學質量以0.8317的置信度被評定為“中等”，即x1∈C3。

已知特征值向量Si=(95，85，75，65，50)，則據公式(7)，教師甲所承擔課程A的課堂教學質量綜合得分為

S=(0.1550，0.2795，0.3972，0.1448，0.0235)·(95，85，75，65，50)T=78.8545。

四、結語

實證分析結果與傳統的專家評分法評價結果對比分析表明，運用AHP、信息熵和置信度識別等理論將復雜的多屬性的定性分析轉化為定量評價，克服了傳統方法的主觀和感性評價的隨意性；與其他定量分析方法評價結果對比分析顯示，該模型采用雙權法進一步提高了模型的效度和信度，更能夠較真實、客觀地反映該教師所承擔的課程A的課堂教學實際水平。雖然計算稍顯復雜，但通過模型的程序化，開發成“教學質量智能評價系統”軟件，能夠進一步提高其可操作性和適應度。

參考文獻：

[1]李俊飛.關于高職院校教師課堂教學質量的理論與實踐[J].高職論叢，2007(1)：34-36.

[2]黃淑蘭，鄭承志.高職院校教師課堂教學質量灰色綜合評價[J].寧波職業技術學院學報，2010，14(2)：46-50.[3]王戰軍.學位與研究生教育評估技術與實踐[M].北京：高等教育出版社，2000.

[4]王彭德，李國虹.標準分在教師課堂教學質量評價中的應用[J].教育測量與評價，2010(1)：27-29.

[5]楊珍，趙利娜，包蘇榮.高校教師教學質量評價方法研究[J].內蒙古農業大學學報：社會科學版，2010，12(1)：91-96.

[6]鄧萬友.高校課堂教學質量的多層次模糊綜合評價模型[J].內蒙古師范大學學報：教育科學版，2010，23(5)：57-60.

[7]黃會明.高職教師課堂教學質量的評價方法研究[J].武漢船舶職業技術學院學報，2013(4)：109-113.

[8]楊運濤.一種教學質量評價新方法[J].科技管理研究，2005(4)：165-166.

[9]華江林.基于粗集理論的教學質量評估系統的研究[D].天津：河海大學，2006.

[10]駱蘭，薛艷，唐國強.論高校課堂教學質量評估指標體系的構建[J].高教探索，2006(6).：55-56.

[11]喻方元.高校教師課堂教學質量評價體系研究[J].高教發展與評估，2008，24(2)：80-85.

[12]胡平波，甘國華.高校教學質量評價指標體系的建設[J].教育學術月刊，2009(12)：50-53.

[13]鄭延福.高校教學質量評價指標的確定[J].統計與決策，2011(2)：165-167.

[14]劉大江.基于未確知測度模型的碾壓混凝土施工質量評價[J].混凝土與水泥制品，2011(8)：65-67.

[15]魏媛.基于AHP法的高校教師教學質量評價體系構建[J].經濟研究導刊，2011(21)：305-307.

(責任編校：李秀榮)

中圖分類號：G64

文獻標志碼：A

文章編號：1672-349X(2016)04-0105-04

DOI：10.16160/j.cnki.tsxyxb.2016.04.020

A Double Weight Quantitative Analysis of Classroom Teaching Quality in Universities

LIU Da-jiang

(College of Civil Engineering， Tangshan University， Tangshan 063000， China)

Abstract：Based on the principles of universality， regularity and applicability，the author of this paper has optimized and integrated many factors affecting classroom teaching quality and established an evaluation system for the classroom teaching quality. Then entropy is employed to compute every index weight， unascertained measure theory is applied to build a comprehensive evaluation model and the comprehensive evaluation value of classroom teaching quality is determined with the AHP method. Tests show that this model is applicable and feasible，and the evaluation result is accurate and objective.

Key Words：classroom teaching quality； double weight quantitative analysis； unascertained measure； entropy