城市公共交通系統(tǒng)中的最佳路徑問題

劉香菊 楊夏青 喬 石 房 麗

（齊魯理工學(xué)院 山東濟南 250200）

?

城市公共交通系統(tǒng)中的最佳路徑問題

劉香菊 楊夏青 喬 石 房 麗

（齊魯理工學(xué)院 山東濟南 250200）

摘 要：通過分析城市公共交通系統(tǒng)網(wǎng)絡(luò)圖的特點，采用改進的Dijkstra 算法的最短路徑問題構(gòu)造公共交通網(wǎng)絡(luò)模型。最佳乘車路線的獲得，需要在滿足換乘次數(shù)要求的基礎(chǔ)上，提出換乘的實現(xiàn)算法，并在此過程中采用用換乘矩陣的形式描述最短路徑中的站點及線路。

關(guān)鍵詞：公共交通系統(tǒng) 最佳路徑 最短路 最小換乘

一、引言

研究公交換乘的問題，首先要解決的問題是合理地表述公共交通網(wǎng)絡(luò)模型；其次還需要對公交換乘問題思想做準確描述［2］。本文將解決換乘算法的實現(xiàn)問題，在此過程中還需綜合考慮換乘次數(shù)的因素，距離因素的影響。

二、城市公共交通系統(tǒng)的特點［3］

與道路網(wǎng)絡(luò)有所不同，城市公共交通系統(tǒng)有其自身特點，公交網(wǎng)絡(luò)不能直接采用與道路網(wǎng)絡(luò)相同的模型。

1.結(jié)點性質(zhì)

在模擬不同公交線可換乘情況［4］時，需要考慮空間上比較接近的不同線路但同名的公交站點的抽象問題。

2.弧段性質(zhì)

由于弧段與屬性之間的一對多的關(guān)系，那么就會導(dǎo)致需重復(fù)記錄在公共交通系統(tǒng)中，每條公交線路通過的弧段，這必然導(dǎo)致數(shù)據(jù)冗余問題的出現(xiàn)。

3.有向線性質(zhì)

由于邊的有向性不能體現(xiàn)公交系統(tǒng)圖有向性特點，因此需要考慮另外的解決方法，即通過引入有向線路集的方法來解決。

三、建立城市公交系統(tǒng)模型

距離最短路段及最少換乘公交線路的集合構(gòu)成了最優(yōu)出行路徑。

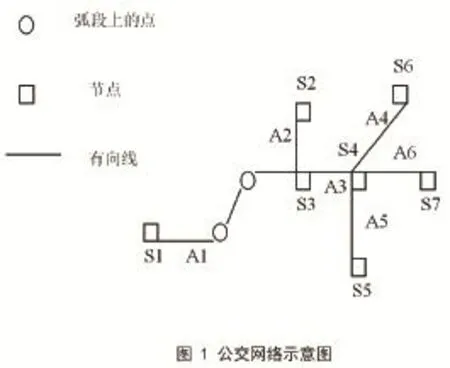
本文將交通網(wǎng)絡(luò)模型采用“結(jié)點―弧段（可有多條弧段）―有向線”的數(shù)據(jù)結(jié)構(gòu)來存儲網(wǎng)絡(luò)圖。公交網(wǎng)絡(luò)如圖1所示。

四、公交換乘問題的解決思想

為解決公交換乘問題，我們需要做下面一些具體工作：

1.求解最短路徑及其上的各個站點。

2.為獲得換乘方案，需先構(gòu)造最短路徑站點及線路對應(yīng)的換乘矩陣，并求解。

五、最短路徑求解

1.經(jīng)典最短路徑算法概述

（1）Dijkstra算法

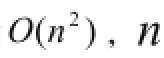
（2）Bellman-Ford-Moore算法

（3）Floyd算法

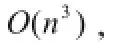
（4）啟發(fā)式搜索算法——A*算法

A*算法提高了搜索過程的效率。引入已知的全局信息作為選擇下一個被檢查的結(jié)點的條件，為合理評價可能性的量度（該結(jié)點處于最優(yōu)路線上的）需對當前結(jié)點距終點的距離作出估計。

2.公交線路查詢不適合采用傳統(tǒng)的Dijkstra算法

但是對公交網(wǎng)絡(luò)來說，由于如下幾方面原因，公交線路的查詢采用Dijkstra算法是不適合的：

（1）數(shù)據(jù)結(jié)構(gòu)復(fù)雜。

導(dǎo)致公交線路網(wǎng)絡(luò)圖的數(shù)據(jù)結(jié)構(gòu)模型復(fù)雜的原因主要是公交網(wǎng)絡(luò)節(jié)點與連通性的特殊性。

（2）算法時間長。

使用基于網(wǎng)絡(luò)的權(quán)矩陣及Dijkstra 算法求解最短路徑問題，在存儲圖形數(shù)據(jù)和進行運算時，需定義由網(wǎng)絡(luò)的結(jié)點數(shù)構(gòu)造的數(shù)組，當網(wǎng)絡(luò)的結(jié)點數(shù)較大時大數(shù)組運算浪費時間。

3.基于改進 Dijkstra 算法的最短路徑求解

由于存在上述的缺陷，采用基于點邊拓撲關(guān)系的最短路徑算法。主要步驟如下：

（1）將目標結(jié)點作為已到達結(jié)點，標志為已到達結(jié)點。

（2）若已到達結(jié)點和起始結(jié)點相同，則執(zhí)行第（6）步，否則執(zhí)行第（3）步。

（3）如果存在未搜索結(jié)點則繼續(xù)第（4）步，否則執(zhí)行第（6）步。

（4）掃描標志為已到達結(jié)點的結(jié)點的關(guān)聯(lián)結(jié)點，這些關(guān)聯(lián)結(jié)點不包括在已搜索節(jié)點表中已經(jīng)存在的結(jié)點。

（5）重復(fù)執(zhí)行第（2）步至第（4）步。

（6）為找出最短路徑，需從起始結(jié)點到目標結(jié)點對所有的已到達結(jié)點對進行追蹤。

六、實現(xiàn)公交換乘的數(shù)學(xué)描述

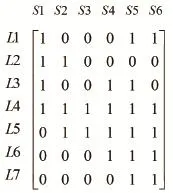
圖 2：矩陣（1）

1.換乘矩陣存儲方式的改進

若公交線路比較復(fù)雜，將導(dǎo)致矩陣（1）規(guī)模很大。公交線路矩陣表也可以作些改進。方法如下：

若最短路徑上剛好包含了某條線路所經(jīng)全部站點，則在該條線路的關(guān)聯(lián)站點數(shù)組中將保存該這條路徑上站點的序號（該站點在矩陣中的位置號）。

如矩陣（1）中線路關(guān)聯(lián)站點數(shù)組，空間浪費會有效減少。

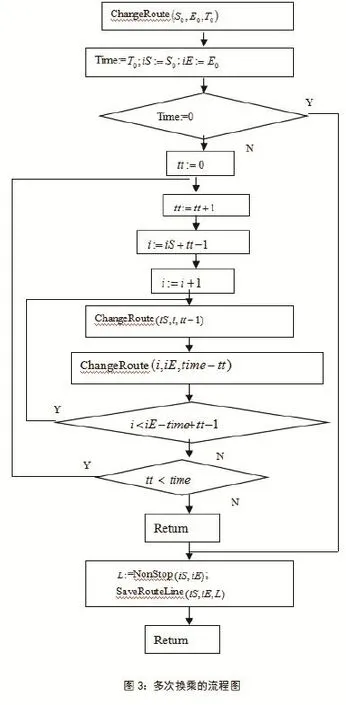
2.多次換乘的實現(xiàn)流程

實現(xiàn)矩陣（1）中任意兩站點之間的換乘的問題的實現(xiàn)方法，可以采用用遞歸方法。具體流程圖如圖3。其中，起始站點在矩陣中的位置號用來表示；目標站點在矩陣中的位置號用來表示；中轉(zhuǎn)次數(shù)為。求解與間的直達線路問題的方法，用來實現(xiàn)。

3.換乘方案的確定

表1 直達數(shù)據(jù)塊列表

最簡單的情形就是0次換乘，通過圖3流程求解出來的直達數(shù)據(jù)塊只有1個，如從起始點A至目標點B，不用換乘。如果直達數(shù)據(jù)塊是不存在的，需要1次換乘的搜索。一次及以上的換乘的情況，得到的直達數(shù)據(jù)塊可能很多。這樣，在直達數(shù)據(jù)塊列表中就存儲了3個直達數(shù)據(jù)塊，如表1所示。

從表1中可以看出，要確定A站點到B站點的換乘方案，次數(shù)更多的方法依此類推。

七、結(jié)論

本文研究乘車路線問題采用的主要理論是最短路徑理論。首先獲得構(gòu)成最短路徑的站點；最佳乘車線路的獲得需要由這些站點及公交線路并采用換乘矩陣的方法。

參考文獻

［1］牛學(xué)勤 ，王煒. 基于最短路搜索的多路徑公交客流分配模型研究［J］. 東南大學(xué)學(xué)報. 2002，32（6），917-919；

［2］楊新苗， 王煒， 馬文騰. 基于城市道路網(wǎng)的最短路徑分析解決方案［J］. 小型微型計算機系統(tǒng)， 2003，24（7），1390-1393；

［3］陳立潮，劉玉樹，張永梅，潘廣貞. 城市交通智能咨詢系統(tǒng)的設(shè)計與實現(xiàn)［J］. 計算機工程， 2003，29（1），32-34；

［4］夏春林 ，蔣瑞波 ，宋偉東. 道路網(wǎng)絡(luò)中最短路徑的算法與實現(xiàn)［J］. 遼寧工程技術(shù)大學(xué)學(xué)報， 2003，22（2）.180-181；

［5］張國強，晏克非. 城市道路網(wǎng)絡(luò)交通特性仿真模型及最短路徑算法［J］. 交通運輸工程學(xué)報.2002，2（3），60-62；