淺談化歸思想在高中數學解題中的應用
隋翔宇
東營市一中,山東 東營 257091
?
淺談化歸思想在高中數學解題中的應用
隋翔宇
東營市一中,山東東營257091
摘要:數學思想的運用可使學生輕松、高效實現頑固性復雜數學難題的解決,極大提高了學生的解題效率。化歸思想是重要的數學思想,同時也是高中數學解題中運用較為廣泛一種數學思想,它既是解題思想,也是一種有效的解題策略,巧用化歸思想,可達到事半功倍的解題效果。本文就如何在高中數學解題中運用化歸思想提出可行性建議,以饗讀者。
關鍵詞:化歸思想;高中數學
所謂化歸思想,即“轉化”與“歸結”。簡單而言,就是人們在數學解題中遭遇困境時,可以將一個問題轉化為另一個問題,即通過轉化手段,歸納為另一個問題,而所轉化與歸納的這一問題恰巧具有可行性的解題策略。這樣,先前的問題便迎刃而解。在高中數學學習中,化歸思想的運用比比皆是,例如,或新知與舊知的轉化、或數與形的轉化、或多元轉為一元、或空間巧化為平面計算等等均是化歸思想的直接表現。
一、巧用“數形轉化”方式滲透化歸思想
化歸思想是一種常見的數學思想方法,高中數學具有枯燥、繁瑣、復雜、艱澀難懂的學科特征,特別是在解題過程中,如果不能盡快理清思路,確定解題方法,復雜問題將會大大挫傷學生解題的積極主動性。而此時如果滲透化歸思想,對難題進行形式或內容上的等價轉化,難題有可能會“柳暗花明又一村”。在高中數學解題中,化歸思想運用的策略有很多,其中數形轉化便是其中一個有效策略。運用數形轉化思想,強化數與形的結合,實現高難度問題的解決是化歸思想的一個重要體現。
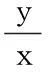
二、注重立體與平面間的轉化,巧解難題
化歸思想是高中問題解決的基本思想,在運用化歸思想的具體過程中,學生應遵循一定的原則,即熟悉化原則、簡單化原則、和諧化原則、直觀化原則等。簡而言之,學生要能使轉化后的問題更加直觀、清晰,問題解決更加方便快捷。在高中數學中,關于立體幾何的題目占據整個高中數學學習內容的一大部分,如何高效解決這些問題成為備受學生與教師關注的話題。運用化歸思想,巧妙將立體幾何轉化為平面幾何,可以大大減低立體幾何問題的抽象、晦澀,促使學生高效解題。
在解答復雜立體幾何問題時,很多學生苦于找不到科學方法,而通過做輔助線、分割、展開、補全圖形等多種方法實現立體幾何向平面幾何的轉化很有必要。有以下一道立體幾何題目:在直棱柱A1B1C1-ABC中,AB AC AB=AC=2,AA1=4,D是BC中點。(1)求異面直線A1B與C1D所成角的余弦值。(2)求平面ADC1與ABA1所成二面角的正弦值。這是一道典型的立體幾何題目,但是在不做輔助線之前,從抽象的立體視角來看,第一問與第二問的解決很困難,但是如果取B1C1的中點D1,然后連接A1D1,BD1就能輕松實現將立體幾何問題轉向平面來解決,問題便會迎刃而解,如下圖所做輔助線:

圖1
由以上例子可知,展開圖形就是將立體圖形通過展開、攤平,使其變為直觀的平面圖形,這樣在立體空間內不容易發現的一些隱含類解題信息便會逐步呈現,這更有利于學生發現某些數量關系,盡快找出答案。
三、常量問題轉化為變量,實現輕松解題
在高中數學學學習中,學生們已經習慣將x作為任何式子中的變量,他們腦海中甚至了已經形成了“x為變量”的定式思維,但是在一些問題中,墨守成規,以“x為變量”的思維很難突破問題解決的瓶頸,這加大了問題的難度。因此,學生要善于在解決某些數學問題時滲透化歸思想,將式子中的變量視為常量,將常量作為變量,獨辟蹊徑,也許會取得不錯的解題效果。
關于常量與變量相互轉化的問題,有以下經典題目:已知實數p,滿足|p|≦2,又含有p的不等式x2+px+1>2x+p恒成立,求x的取值范圍。很多學生在做此題時,很容易將該題目認為是含有變量x與常量p的不等式求解,但如果一旦運用該思想進行求解,便會發現難上加難。反之,如果轉變思維,注重將式子中的x視為常量,將p作為變量,可以簡化求解過程,問題便簡單很多。具體而言,可將原式子化為關于p的一元一次不等式p(x-1)+(x-1)2>0即f(p)=p(x-1)+(x-1)2,這樣就將原式子輕松轉化為以上一元一次不等式,最終解得x<-1,或x>3。由以上的例子可知,解題時將常量問題轉化為變量,更容易實現問題的輕松解決。誠然,該方式是化歸數學思想的重要體現,學生們解題過程中如果遇到類似題目,要巧用化歸思想,實現常量與變量間的轉化。當然,常量轉為變量并不適合所有題目,教師在解題過程中應酌情使用。
綜上可知,化歸思想應用于高中數學解題,不僅能幫助學生理清思路、找準解題方向,更能活化學生思維,啟迪學生智慧,提升學生能力,最終使其養成運用數學思想方法解決數學難題的習慣。誠然,這不僅對學生高中數學學習有促進作用,甚至還能為學生以后的數學學習奠定堅實的基礎。在高中數學數學解題中運用化歸思想,要求學生巧用數形轉化、立體平面轉化、常量變量轉化等策略,實現數學難題的解決。當然,在具體的解題過程中,學生要懂的融匯貫通,隨機應變,充分發揮化歸數學思想的效用。
[參考文獻]
[1]任興發.化歸思想在高中函數教學中的應用研究[D].內蒙古師范大學,2013.
[2]楊社鋒.化歸思想在高中數學解題中的應用[D].河南大學,2014.
[3]鮑怡.化歸思想方法在中學數學教育中滲透的案例研究[D].蘇州大學,2009.
中圖分類號:G633.6
文獻標識碼:A
文章編號:1006-0049-(2016)14-0210-01

