初中數學教學中數形結合思想的滲透

石澤定

（坪壩鎮九年制學校 湖南古丈 416301）

初中數學教學中數形結合思想的滲透

石澤定

（坪壩鎮九年制學校 湖南古丈 416301）

數形結合思想是初中課本中的基本數學思想，在初中數學教學中扮演著十分重要的角色。本文結合了本人的一些教學體會，分析了如何充分利用數形結合思想在教學中的運用以及去解常見數學題目，使學生充分認識“數”和“形”之間的內在聯系，把問題化繁為簡，化難為易，使學生在學習數學知識中，充分了解和掌握數形結合這種解決問題的策略和方法。

數形結合 思想 解題

引言

數形結合思想在初中數學中應用廣泛。初中數學最初是從有理數、相反數和絕對值開始的，尤其是數軸的引入是數形結合思想的一個重要展現。因為對任何一個有理數來講，數軸上都有唯一一個點與它對應，然后通過這種對應來規范它們的關系。這樣通過滲透數形結合的思想方法，能夠幫助學生正確理解有理數的意義及其運算。數形結合的思想給學生拓寬了解題思路，讓數學變得不再枯燥。在日常的教學工作中，我主要是從以下幾個方面解決常見問題的：[1]

一、運用圖形的直觀解決數量關系

在數學這一學科中數和形是一種對應關系，對于初中的孩子來說數字永遠是枯燥乏味的概念，人人都難以把握，而形就不同了，它具有直觀形象的特點，對解決問題起決定性作用，因此我們找到數形的對應關系利用圖形來解決問題可以讓復雜的問題簡單化。

例1：分解因式：a2?b2這個分解因式的題目非常簡單，是同學們非常熟悉的公式——平方差公式：a2?b2=(a+b) (a?b)，有時也就是直接用這個公式來套用進行分解因式的。但是有不少學生卻不能理解a2?b2=(a+b) (a?b)這個公式？有些同學雖說理解，但也是從整式乘法公式(a+b) (a ?b)=a2?b2的逆用來理解的，相當于死記硬背來掌握的。理解平方差公式a2?b2=(a+b) (a?b)，我們可以從幾何圖形出發來理解。

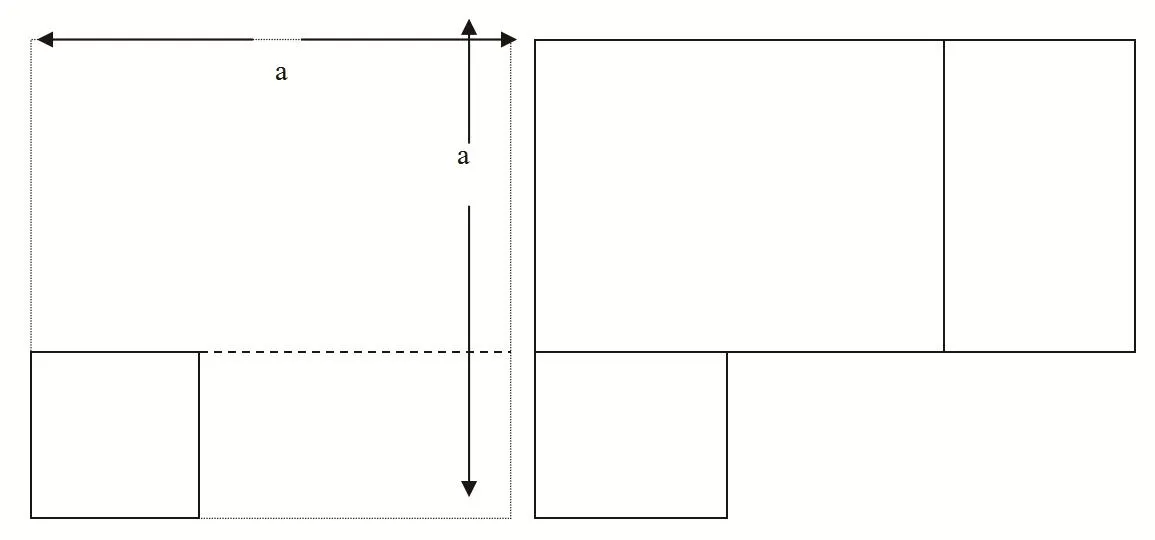
如左圖，在邊長為a的正方形紙板中剪去一個邊長為b的小正方形后，剩余圖形的面積是（a2?b2），把左圖的剪下小正方形后的剩余圖形拼在一起，得到右圖，是一個長方形，其長為（a+b），寬為（a-b），面積為（a+b）（a-b），所以可以得到a2?b2=(a+b) (a?b)。

其實除了理解平方差公式的意義可以用幾何圖形面積來幫助分析外，還有完全平方公式等其它的整式乘法公式或分解因式公式，可以用幾何圖形面積來幫助理解其意義。

A、3 B、2 C、1 D、0

分析：直接化分式方程為整式方程，確定方程根的個數，是十分困難的事，結合問題特征，要將“數”轉達化成“形”去研究。

解：把方程化為拋物線

y1=?x2+5x+2與雙曲線分別畫出草圖，在x>0的范圍內，兩函數圖象有兩個交點。

通過這種“數”與“形”的轉化，使本來很難解的題目，變得解起來得心應手了。解此類題目，主要是我們是否能夠把代數問題轉化為幾何問題，把握得很好。也就是說，這些代數問題怎樣轉化到幾何性質問題上來，才是解題的關鍵。

二、利用數量關系揭示幾何圖形的性質

雖然形形象、直觀，但還必須借助代數的計算進行定量研究，尤其是較復雜的“形”，把圖形數字化做正確是一件有難度的事情，這就要求用心觀察圖形，掌握它的特點，將隱含條件找出來，把“形”正確表示成“數”的形式，進行分析計算。

例3、等腰三角形的面積為2，腰長為5，底角為，求tanα。

分析：本題是斜三角形問題，因此要作高化斜三角形為解直角三角形。但是本題又沒有給出三角形的形狀，所以在畫高時就要考慮高在三角形內、三角形上和三角形外三種情況，這是一種解題方法，但非常麻煩，我們可以考慮用數形結合的思想來解決本題，用數學中的方程或方程組來解。

本題應用了數形結合思想，“形題數解”往往可以使求解思路新穎，而且幾何中的多解問題可以轉化為方程或方程組的多解問題。

例4、用黑白兩種顏色的正六邊形地面磚按如下的規律，拼成若干個圖案：

（1）第四個圖案中有白色地磚＿＿＿＿＿＿＿塊；

（2）第n個圖案中有白色地磚＿＿＿＿＿＿＿塊。

分析：本題是借助于圖形中的數量關系來解決問題，第一個圖案中有白色地磚6塊，第二個圖案中有白色地磚10塊，第三個圖案中有白色地磚14塊，根據前面的分析，很快就能判斷出第四個圖案中有白色地磚18塊，并且每個圖案比前一個圖案增加4個白色地磚，所以第n個圖案中有白色地磚4n+2塊。

北師大版七年級數學上冊第三章“字母表示數”，本章的不少小節的內容是探索幾何圖形（或幾何圖案）的數量關系，教學中，老師指導學生會用代數式表示幾何圖形（或幾何圖案）的數量關系，老師若注重了數形結合思想方法的滲透，會使學生很快領悟幾何圖形（或幾何圖案）的規律，從而找出其中的數量關系。

三、將數量關系和圖形的性質，在解題中串連結合使用

“數”與“形”既是數學教學中兩個對立面，最終還得為解決問題達成一個統一。觀察圖形的形狀，從感觀上認識問題，深入分析數與式的結構，引起聯想，適時將它們相互轉換，將抽象的數字變化為直觀的形象，進而揭示其中隱含的數量關系。數形結合的基本思想方法，就是在探究問題的過程中，注意把數和形作這一個統一體結合起來考察，在大腦中形成一個具體的意向，把圖形的性質問題轉化為數量關系的問題，或者把數量關系的問題轉化為圖形性質的問題，使復雜問題變簡單，抽象問題更形象，將難度系數降低，運用簡單易行的方法獲得解決問題的途徑。

不久前在給學生中考復習過程中，遇到了這樣的一個題目：

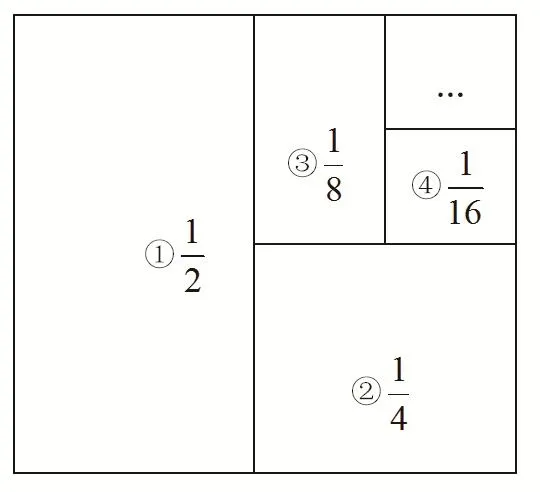
我們可以這樣理解，用剪刀去剪這個正方形紙片，第一次剪去正方形紙片的一半，正方形剩余面積是，第二次剪去剩余圖形的一半，得到的圖形面積是第三次剪去第二次剪剩的圖形的一半，得到的圖形面積是即每次剪去前一次剩余圖形面積的一半，……那么當第n次剪后得到的圖形面積是，把每次剪下來的圖形面積相加，即得到

總而言之，“數無形不直觀，形無數難入微” 。見到數量就要考慮它的幾何意義，見到圖形就應考慮它的代數關系，運用數形結合的思想解決數學問題。因此數形結合思想在初中數學教學中起著舉足輕重的作用。

[1]沈文選； 中學數學思想方法；湖南師范大學出版社；1999.5

[2]2008安徽省中考經典頭名卷數學；安徽教育出版社； 2008.2