行為保險學系列(五)伯努利效用函數的修正與保險決策
郭振華 上海對外經貿大學金融學院
行為保險學系列(五)伯努利效用函數的修正與保險決策
郭振華上海對外經貿大學金融學院
本文受國家自然科學基金面上項目(71173144)的資助。

郭振華,上海對外經貿大學金融學院保險系主任、副教授,兼任中國保險學會理事、上海保險學會理事。長期講授《保險學》《保險公司經營管理》等課程,主持完成國家自然科學基金、教育部社科基金、上海社科基金項目各一項。
如“行為保險學系列(一)理性保險決策理論及其由來”所述,在新古典經濟學和當今主流經濟學教材中,一直采用的是伯努利1738年發明的效用函數。在人類世界,伯努利首次將財富的“金錢價值”和財富帶來的“效用(心理價值)”區分開來,用邊際遞減的效用函數解決了圣彼得堡悖論,成為理性人進行風險決策的經濟學準則。
伯努利效用函數有四大特點:第一,個體的效用是由其財富狀態或財富結果決定的;第二,只要個體擁有一定的財富,無論規模大小,都會有一定的正效用水平;第三,隨著財富增加,個體的效用會增加,但財富增加帶來的邊際正效用遞減;第四,隨著財富減少(或損失增加),個體的效用會降低,但人們的邊際負效用遞增。
表1是伯努利于1738年計算得出的一個效用函數版本,從中可以清晰地看到上述四個特點:第一,不同的財富值帶來不同的效用值。100萬達克財富水平的效用值是10個點,200萬達克財富水平的效用值是30個點。第二,只要個體擁有一定的財富,無論規模大小,都會有一定的正效用水平。可以看到,無論財富多少,效用值都是正的。第三,隨著財富增加,效用增加,但邊際正效用遞減。例如,財富水平從100萬達克增加到200萬達克時,效用增加了20個點(= 30-10);財富水平從200萬達克增加到300萬達克時,效用只增加了18個點(=48-30);財富水平從900萬達克增加到1000萬達克時,效用只增加了4個點(=100-96)。第四,隨著財富減少,效用降低,但邊際負效用遞增。例如,財富水平從1000萬達克降低到900萬達克時,效用減少了4個點(= 100-96);財富水平從900萬達克降低到800萬達克時,效用降低了6個點(=96-90);財富水平從200萬達克降低到100萬達克時,效用大幅減少了20個點(=30-10)。
本文討論效用函數對保險決策的影響,而保險主要承保純粹風險,純粹風險的特點是“要么遭受損失、要么沒損失”,所以,本文主要研究個體在損失情境下的效用函數。在揭示伯努利效用函數缺陷的基礎上,修正了損失情境下的效用函數,討論了修正后的效用函數對保險決策的影響。
一、“財富值決定效用值”有誤:未考慮參照點的影響

?表1 伯努利1738年計算的效用函數
伯努利認為,一定的財富狀態或財富值對應一定的效用水平,一定的效用水平代表著一定的快樂程度。如果A和B具有相同的伯努利效用函數,則,只要其財富水平相同,A和B的快樂程度就應該相等。但事實并非如此。
1.財富值相同,效用未必相等
案例1:假定張三和李四具有相同的伯努利效用函數,現在擁有相同的財富水平400萬元,按照伯努利的效用理論,張三和李四的效用水平相同,快樂程度也應該相同。
但是,想想兩人在400萬元財富之前的狀態吧!假定張三之前擁有200萬元,李四之前擁有600萬元,那么,張三和李四現在的快樂程度相同嗎?答案是顯然的,張三由于財富翻倍而非常高興,李四則由于財富劇烈縮水而非常失望!所以,伯努利效用理論的預測是錯誤的。
再假定張三之前擁有1000萬元,李四之前擁有500萬元,現在兩人擁有相同的財富400萬元。則,按照伯努利的效用理論,兩人現在的快樂程度應該是相同的,但實際情況是,張三明顯比李四更加失望。伯努利效用理論的預測再次出現失誤。
2.財富值為正,效用可能為負
按照伯努利效用函數,無論從過去到現在財富是增加還是減少,只要個體現在有一定的財富,他就有一定的正效用或一定的快樂程度。
但事實上,通過案例1可以發現,個體會將現在與過去進行對比,財富增加會使個體變得快樂(獲得正效用),財富減少會使個體變得悲傷(獲得負效用)。但伯努利效用函數未考慮人類會因財富減少而悲傷這一狀況,因此,伯努利的效用理論是有缺陷的。
3.參照點不但重要,還會移動
從案例1可以看出,過去財富水平(或初始財富)基礎上的財富變化決定著人們的效用和快樂程度,這個過去財富水平或初始財富是個體進行決策的參照點。卡尼曼和特沃斯基曾通過如下選擇問題證明了參照點的巨大作用和伯努利理論的缺陷。
問題1:不管你原來有多少錢,現在再給你1000美元。請你在如下兩個選項中選擇一個:
A.50%的概率贏得1000美元,50%的概率什么也得不到;
B.肯定得到500美元。
問題2:不管你原來有多少錢,現在再給你2000美元。請你在如下兩個選項中選擇一個:
A.50%的概率損失1000美元,50%的概率損失為零;
B.肯定損失500美元。
可以看出,問題1和問題2帶給被試者的財富的最終狀態是相同的,本質上都相當于請被試者在如下問題中做出選擇:
A.50%的概率贏得2000美元,50%的概率得到1000美元;
B.肯定得到1500美元。
按照伯努利效用理論,被試者對問題1和問題2應該做出相同的選擇“B”。但事實上,對于問題1,多數被試者會選擇B,但對于問題2,多數被試者會選擇A,這就是參照點在起作用。對于問題1,被試者的參照點是“現有財富+1000美元”,并將選擇編輯為盈利的風險問題;對于問題2,被試者的參照點是“現有財富+2000美元”,并且將選擇編輯為損失的風險選擇問題。由此導致了與伯努利效用理論預測截然不同的選擇結果。顯然,人類在決策中不僅會考慮參照點,還會經常移動自己的參照點,不考慮參照點的伯努利效用理論在對人類選擇的預測上面臨困境。
4.參照點對個體決策的重大影響
在上述案例中,伯努利效用函數僅考慮財富結果對效用的影響,沒有考慮到個體會因財富變化而影響自己的效用水平或快樂程度(或悲傷程度),而財富變化必然有一個基準點,卡尼曼和特沃斯基將這個基準點稱為“參照點”。正是基于參照點(往往是現狀)的財富變化影響了人們的效用水平或快樂程度,人們的參照點才會隨時發生變化,最終導致基于參照點的決策發生變化。
1979年,卡尼曼和特沃斯基在其發明的前景理論(ProspectTheory)中提出:第一,效用是隨著財富的變化而出現的,而不是隨著各種財富狀態而出現的。或者說,財富狀態本身并不帶來效用,財富的變化才會帶來效用;第二,既然考慮財富變化,就一定要考慮參照點,關注的是從參照點開始的變化;第三,變化自然會有兩個方向,財富增長是贏,財富縮水是虧,財富增長帶來正效用或快樂,財富縮水帶來負效用或悲傷。這與人們在面對選擇時的心理過程是極為類似的。
二、“財富減少導致邊際負效用遞增”有誤
在伯努利效用函數中,隨著財富減少(或損失增加),個體的邊際負效用遞增,如表1所示,財富水平從1000萬達克降低到900萬達克時,效用減少了4個點;財富水平從900萬達克降低到800萬達克時,效用降低了6個點;財富水平從200萬達克降低到100萬達克時,效用大幅減少了20個點。但是,由于以下兩點原因,“財富減少,個體的邊際負效用遞增”這一說法站不住腳。
1.人們在面臨損失風險時,往往呈現風險喜好
考慮下面的選擇問題:
A.50%的概率損失1000美元,50%的概率損失為零;
B.肯定損失500美元。
按照伯努利效用函數,人們應該選B。因為在伯努利效用函數中,無論是盈利風險還是損失風險,個體的效用函數為凹函數,呈風險厭惡態度,財富期望值的效用總是大于財富效用的期望值,假定初始財富為W0,即
U(B)=U(W0-500)>U(A)=50%×U(W0-1000)+ 50%×U(W0)
但實際上,多數人都會選擇A,這如何解釋呢?可能的解釋就是,人們在面臨損失風險(純粹風險)時,其效用函數是凸函數,呈風險喜好態度,隨著損失增加,邊際負效用遞減,在將現有財富W0作為參照點的情況下,人們會認為:
U(B)=U(-500)<U(A)=50%×U(-1000)+50%×U(0)
2.無論財富增減,個體感受都遵從費希納定律
心理學家很早就想知道當客觀事物變化時,人們對客觀事物的體驗到底是如何變化的,例如,當水的溫度、光的強度等物理量變化時,人們對水溫和光的強度的主觀體驗值是如何變化的,這一領域稱為心理物理學(Psychophysics)。
關于心理物理學,心理學家們最早提出的問題是,究竟物理刺激的強度變化多少才能讓個體感覺到有差異,或者感覺到確實發生變化了。例如,室內燈光增加(或減少)多少瓦時,個體才能感覺到光線增強(或減弱)了。1834年,韋伯(Weber)提出,總的來說,某一種物理刺激,若要使人感覺到其強度的增加(或減少),必須使這一物理刺激強度在原有基礎上增加(或減少)某個百分比,這一變化量被稱為“最小可覺差”。于是,對于較小的物理刺激來說,只需要增加較小的變化量,個體就可感知到變化;但對于已經較大的物理刺激,就必須增加較大的刺激量,才能引起同等程度的注意。為了達到最小可覺差,需要增加(或減少)的刺激強度與原刺激強度的比率稱為“韋伯分數”。舉例來說,對重量差異感知的韋伯分數接近1/30,即只有將負重增加(或減少)原有負重的1/30時,人類才能感覺到負重確實增加(或減少)了。事實上,對于特定類型的感官刺激,其韋伯分數基本保持恒定,這一規律被稱為“韋伯定律”。
1860年,心理學家費希納(Fechner)提出,最小可覺差可以用一定數值的心理強度而不是物理強度來描述,并且認為,心理強度是物理強度的對數,這稱為“費希納定律”。這一定律后來被廣泛接受,從此,心理強度指標逐漸走上歷史舞臺。例如,噪音的心理強度現在用“貝爾”或“分貝”(1貝爾=10分貝)來衡量,“貝爾”是一個心理強度指標而非物理強度指標,其計數單位就是以物理振幅的對數值來定義的,即“噪音的心理強度=log噪音的物理振幅”,噪音每增加1貝爾,表示物理振幅增大了10倍。費希納定律所描述的對數函數的圖形見圖1。
對數函數顯然遵循邊際遞減原則,也叫做邊際報酬遞減定律。經濟學家們提出,這個定律不僅適用于描述心理強度與物理強度之間的關系,也適用于描述金錢與效用之間的關系。事實上,天才伯努利早在1738年就提出,金錢與效用之間的關系服從邊際報酬遞減定律(細節上與費希納定律有所不同),比心理學界的費希納定律早了120多年。1979年,卡尼曼和特沃斯基將心理物理學中的邊際報酬遞減定律運用到了前景理論中,認為,無論在參照點的右側還是左側,或者無論是收益變化還是損失變化,其引起的效用變化都服從邊際遞減定律。
3.小結:損失情景下邊際負效用遞減
基于以上兩點原因,尤其是基于心理物理學的研究成果,伯努利效用函數中財富減少帶來的邊際負效用遞增的結論是錯誤的,財富減少帶來的邊際負效用也是遞減的。而邊際負效用遞減的函數,正好可以用來解釋人們在面臨損失風險時所呈現的風險追求行為。
三、損失情景的效用函數與保險決策
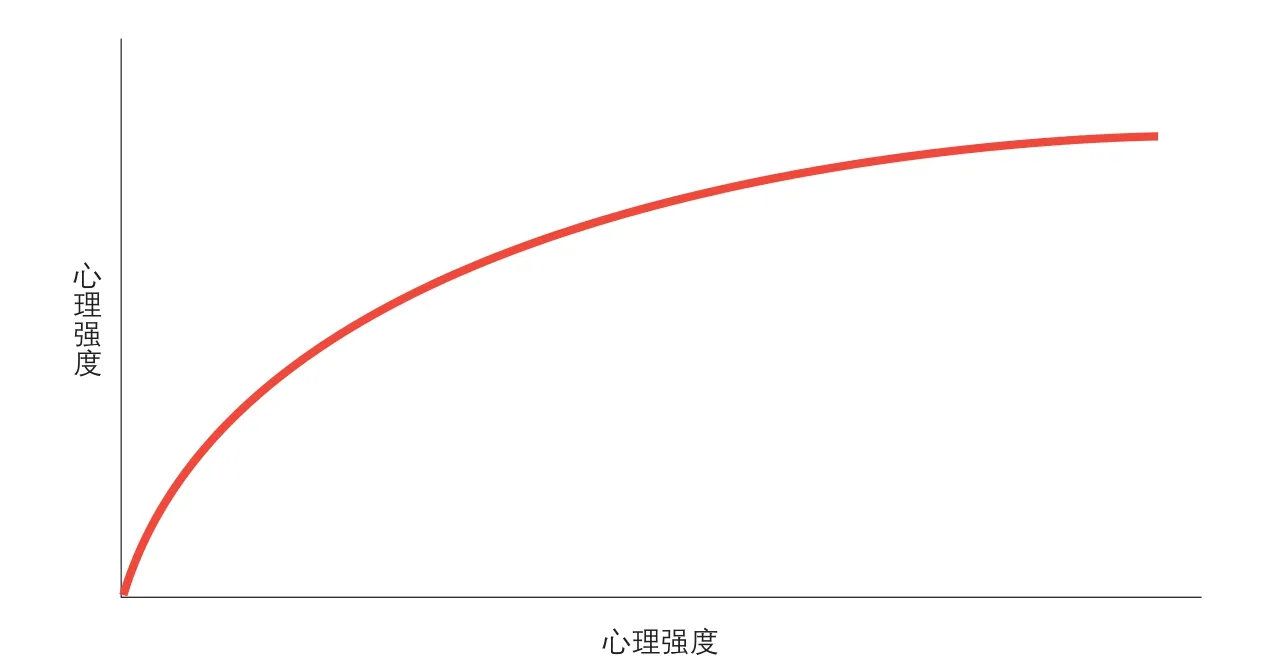
?圖1 費希納定律:心理強度與物理強度的對數函數關系
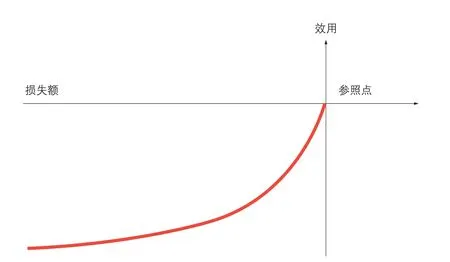
?圖2 損失情景的效用函數
1.損失情景的效用函數:邊際負效用遞減
如上所述,效用函數應該考慮參照點,財富減少帶來的邊際負效用遞減。因此,損失情境下的效用函數如圖2所示。損失情境下的效用函數呈現三個特點:第一,自變量“損失額”為基于參照點的負向變化,是負值;第二,因變量“效用”是負效用;第三,效用函數為凸函數,顯示出邊際負效用遞減,即隨著損失增加,個體對損失的敏感度降低。

2.保險決策:個體不愿投保
在損失帶來負效用,損失部分的效用函數為凸函數的情況下,相較于伯努利效用函數(凹函數),在其他條件不變的情況下,人們的保險決策發生了重大變化,如圖3所示。
在伯努利效用函數下,在保險公司僅收取純保費或附加保費不高的情況下,人們愿意投保;但在如上凸效用函數下,即便保險公司僅收取純保費,人們也不愿意投保。如圖3所示,假定個體面臨以的概率p損失L的風險,參照點為現狀,保險公司僅收取純保費pL。則,
U不投保=pU(-L)>U投保=U(-pL)
人們的選擇將是不投保。如果保險公司還要收取附加保費,不投保的效用U不投保不變,但投保的效用U投保會沿著效用函數曲線繼續向左下方移動,人們更加不會選擇投保。個體的保險決策如表2所示。
四、結論
第一,伯努利效用函數存在兩大缺陷:一是未考慮參照點的影響;二是在損失情境下邊際負效用是遞減而非遞增。上述兩大缺陷導致伯努利效用函數無法解釋人們的喜怒哀樂,與現實嚴重脫節。
第二,在與保險決策相關的損失場景下,修正后的效用函數如圖2所示,這也就是卡尼曼和特沃斯基發明的前景理論中價值函數的左半部分,呈邊際負效用遞減。
第三,在其他條件不變的情況下,邊際負效用遞減的效用函數將導致人們普遍不愿投保,無論保險公司是否收取附加保費。
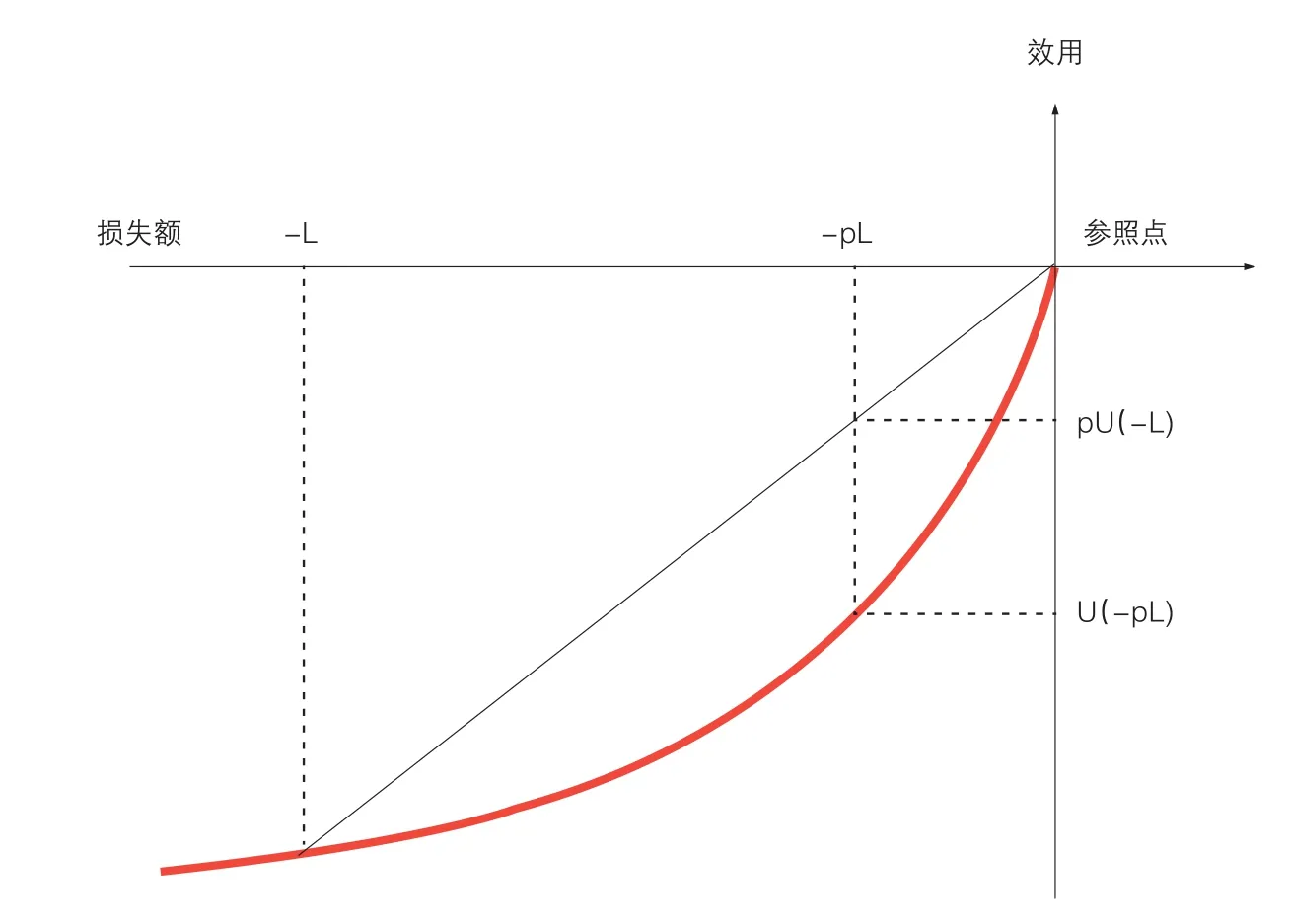
?圖3 凸效用函數下的保險決策

?表2 不同效用函數條件下的投保決策

