提煉·抽象·簡化·應用

黃紅成

摘要：數學是模式的科學。把握數學模型的類型，掌握數學模型的建構方法，讓學生運用數學模型解決問題以形成初步的模型思想是數學教學的應然舉措和重要任務。

關鍵詞：數學模型；類型：建構；要點

數學是模式的科學?！稊祵W課程標準（2011年版）》在“課程設計思路”中明確指出.數學教學要讓學生體驗從實際背景中抽象出數學問題、建構數學模型、尋求結果、解決問題的過程。同時，新課程又大力倡導“問題情境——建立模型——解釋、應用與拓展”的“問題解決”式學習模式。因此，把握數學模型的類型，掌握數學模型的建構方法.讓學生運用數學模型解決問題以形成初步的模型思想是數學教學的應然舉措和重要任務。

一、數學模型的呈現類型

數學模型有廣義和狹義之分。張奠宙認為，“廣義上講，數學中各種基本概念和基本算法，都可以叫做數學模型?！豹M義上理解，只有反映特定問題和特定具體事物系統的數學關系結構，才能稱之為數學模型。在當下的小學數學課堂教學（或教材）中，由于受學生知識視野、認知方式等因素的影響，數學模型的呈現通常表現為這樣三種類型。

1.文字描述。文字描述是數學教材呈現數學模型的重要方式。很多數學概念、性質通常都采用語言文字來進行描述。例如等式的性質呈現為“等式的兩邊同時加上或減去相同的數，所得結果仍是等式”和“等式的兩邊同時乘或除以相同的數（0除外），所得結果仍是等式”。

2.符號表述。符號表述也是數學教材呈現數學模型的常見方式。一些數學定律、性質也常常借助數學符號來揭示個中特定的數量關系和變化規律。例如加法結合律呈現為“（a+b）+c=a+（b+c）”，乘法分配律呈現為“a×（b+c）=a×b+a×c”。

3.圖形概述。圖形概述是數學模型呈現方式一種必要補充。有些數學概念較為抽象，文字描述不便于學生把握概念的本質，可以借助圖形來幫助學生理解概念的意義。例如小數的意義.可以借助“把一條線段或一個長方形平均分成10份，表示其中一份或幾份的部分可以寫成一位小數”的方式來幫助學生理解小數的意義。

二、數學模型的建構方式

數學建模就是建立數學模型的過程，包括對實際問題進行提煉、抽象、簡化，以及確立、解釋、應用和拓展數學模型等過程。數學教學，需要幫助學生建立數學模型，給學生創造借助數字、字母、圖形等媒介來表示各種現象或規律中的數學結構的機會.給學生搭建感悟、理解數學模型和運用數學模型解決問題的舞臺，進而讓學生深刻把握數學的本質和形成初步的數學模型思想。

（一）提煉問題，建構模型

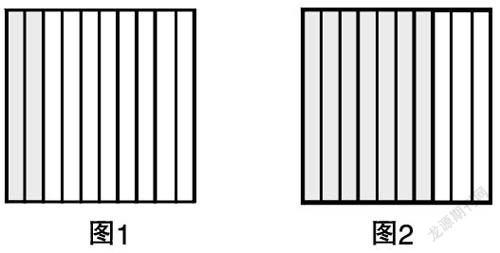
從所發揮的作用角度審視，數學模型揭示了數學對象或問題的本質屬性和共同特征。所以教學中，需要引導學生對數學對象或問題進行對比分析，采用合適的方式表現出對象或問題中的共同屬性，利于學生把握數學問題的本質。例如在教學小數的意義時，課始筆者直接出示圖1：

師：把整個正方形看做“1”，涂色部分用哪個分數表示？

生：2/10。

師：為什么可以用2/10表示？

生：因為平均分成了10份，表示其中的2份。

師：其中2份除了可以用2/10表示，也可以用小數0.2表示（板書：2/10，0.2）。

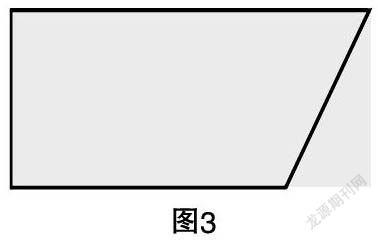
出示圖2。

師：這樣的7份用哪個分數表示？

生：7/10。

師：也可以用小數0.7表示（板書：7/10，0.7）。這樣的5份可以用哪個小數表示呢？

生：0.5。

師：想一想，0.9用圖怎樣表示？

生：把一個正方形看做“1”，平均分成10份，涂其中的9份。

師：這里的9份用分數怎樣表示？

生：9/10。

師：比一比這些分數，有什么相同的地方？

生：都表示十分之幾。

師：分母是10的分數還可以用什么表示？

生：小數。

分析上面的片斷，結合兩個圖形，先讓學生用分數表示其中的涂色部分，然后引出小數的表示方法.再讓學生思考小數用圖形怎樣表示等問題。這樣教學，采用了直觀教學的方式，避免了學生對枯燥的小數意義的掌握和理解。同時在比較表示涂色部分的分數異同的過程中，讓學生迅速感悟到分母是10的分數也可以用小數來表示。并且這些圖形也可以看成是這些小數的數學模型，有利于學生形象地把握小數的本質意義.為后面更復雜的小數意義的認識和小數的大小比較做了充分的鋪墊。

（二）抽象對象，建構模型

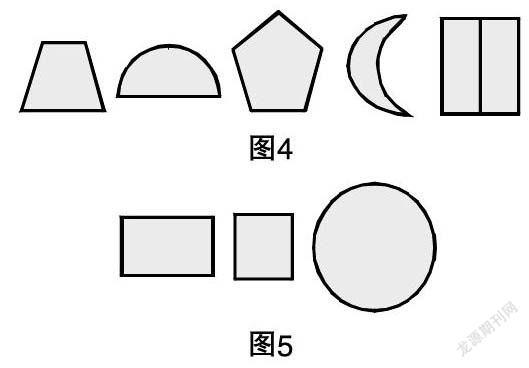
在小學階段.受小學生學習能力的左右.教學材料和教學手段通常都是直觀易感的，也容易使學生對問題的認識滯于淺表，只有適時對直觀的學習材料進行抽象.才能提高學生對數學問題或概念的認識.達到準確把握數學本質的教學目的。例如在教學《認識周長》讓學生理解周長的意義時，筆者首先創設了灰太狼繞長方形操場一周的情境（紅線是灰太狼行走的路線，如圖3）。

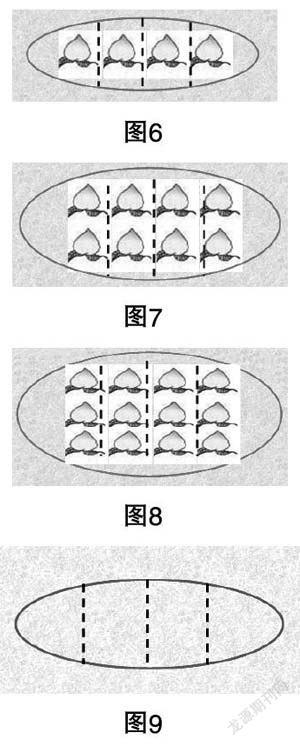
讓學生回答第一次為什么不是繞操場的一周的原因.繼而初步判斷什么是圖形邊沿的一周.然后再讓學生用彩筆描下面圖形的一周（如圖4）。

師：第5幅圖形的一周在哪兒？誰來指一指！

學生上前指示。

師：中間的豎線是整個長方形的一周嗎？

生：不是！

師：比較一下，下面三個圖形一周的長度一樣嗎？哪個最長？哪個最短？

出示圖5。

生：不一樣！圓形一周的長度最長，正方形一周的長度最短。

師：圓形一周的長度最長也就是指它的周長最長，那正方形什么最短呢？

生：周長。

師：誰能用一句話來說一說，什么是圖形的周長？

生：圖形邊沿的長度叫做周長。

生：圖形一周的邊線的長度叫周長。

生：圖形一周的長短叫做它的周長。

周長的概念是抽象的.教材通常采用“（封閉）圖形一周的長短叫做它的周長”的文字來表述周長的數學模型，而且學生也難以從單一的教學材料中感悟到的周長的意義。審視上面的教學過程.筆者讓學生經歷了幾個不同層次的學習活動，讓學生先初步判斷，然后感受和體驗“什么是圖形的一周？什么不是圖形的一周？圖形的一周有的長有的短”的過程，使得學生即使脫離具體的圖形和學習活動，也能比較準確地理解抽象的文字所表述的數學模型的真正含義。

（三）簡化背景，建構模型

數學建模的過程是一個逐步抽象、逐漸簡化的“數學化”的過程。教學時，可以采用變式的方式，不斷變化數學問題的背景或非本質屬性，并在變化中建構出數學問題的數學模型，進而突出數學問題的本質意義。例如三年級下冊的《認識分數》，要讓三年級的小學生準確而深刻地理解“把一些物體看成一個整體平均分成若干份，其中的一份或幾份也可以用幾分之一或幾分之幾來表示”是存在一定認知困難的。為了突破這樣的教學難點.筆者進行了如下教學——

出示主題圖中的問題：把一盤桃平均分給4只小猴，每只小猴分得這盤桃的幾分之幾？

師：如果盤子里只有1個大桃，要平均分給4只小猴，那就需要平均分成幾份？每只小猴分得幾份？是這盤桃的幾分之幾？

生：4只小猴，平均分成4份，每只小猴分得1份，是這盤桃的1/4。

師：如果這盤桃有4個，每個一樣大小。咱們是把每個桃都平均分成4份然后分給小猴.還是把它們看成一個整體來平均分？

生：看成一個整體。

師：看成一個整體，我們需要用集合圈把它們圈起來。

媒體演示。

師：還得平均分成幾份？每只小猴分得幾份？是這盤桃的幾分之幾？

生：平均分成4份，每只小猴分1份，是這盤桃的1/4。

出示圖6。

師：如果這盤桃有8個。把它們看成一個整體怎樣表示？

生：用個圈圈起來。

師：把這個整體平均分成幾份？每只小猴分得幾份？是這盤桃的幾分之幾？

生：平均分成4份，每只小猴分l份，是這盤桃的1/4。

出示圖7。

師：如果這盤桃有12個，你能回答這個問題嗎？

生：把12個桃看成一個整體平均分成4份，每只小猴分得1份，是這盤桃的1/4。

出示圖8。

師：還需要再變一變嗎？為什么？

生：不需要。因為不管盤子里有幾個桃.只要平均分成4份，每份都是這盤桃的1/4。

師：既然跟這盤桃的數量沒有關系，咱們就隱去這些桃的個數。

出示圖9。

師：如果每份中都放4個桃，每份還是這個整體的1/4嗎？5個桃呢？7個蘋果呢？

……

在這個過程中，筆者結合“想知道這盤桃有幾個嗎”的問題引發學生對這盤桃的個數的思考，然后帶領學生依次確定和變化桃子的個數解決“每之小猴分得這盤桃的幾分之幾”.使學生認識到“不管盤子里有多少個桃，只要平均分成4份，每份都是這盤桃的1/4”。如此操作，將具體的教學實例逐漸簡化、抽象成數學模型（見圖10中的圖形），不但減小了學生的認知困難，也實現了學生對分數意義的認知飛躍，從而深刻地把握了分數意義的本質。

（四）探索應用，建構模型

建構數學模型是解決問題的需要.它是學生學習的數學思想方法和解決問題的有效手段，能夠提高學生的數學能力。有些數學知識僅表示一種數學模型的一個方面，學生初步認識時不便建構出數學模型，而在應用過程中逐漸體現數學模型的作用，生發建構數學模型的需要。例如公倍數和公因數，教材呈現了這樣兩個問題：

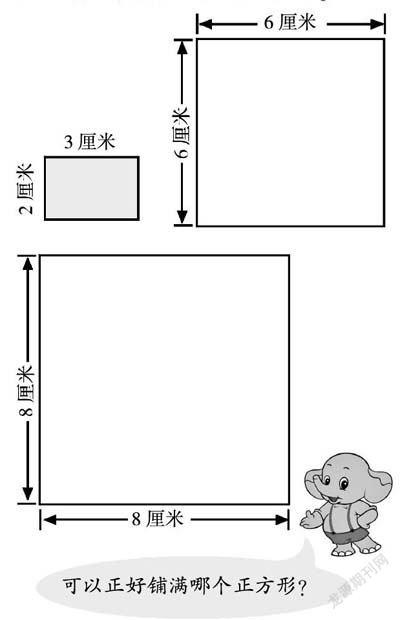
例1 用長3厘米、寬2厘米的長方形紙片分別鋪右邊的兩個正方形。

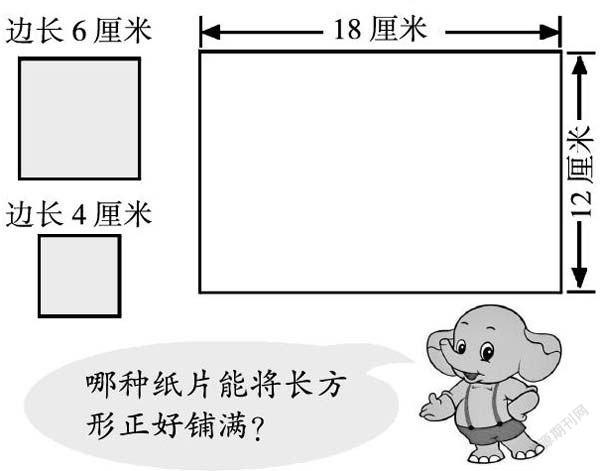
例2 分別用邊長6厘米和4厘米的正方形紙片鋪右邊的長方形。

可以說，兩個例題中的兩個圖形（左圖中邊長6厘米的正方形和右圖中的長方形）就是公倍數和公因數的數學模型。在教學時，為了讓學生清晰地理解公倍數的意義，教材通常從文字敘述“某數既是一個數的倍數又是另一個數的倍數，那么某數就是這兩個數的公倍數”和“某數既是一個數的因數又是另一個數的因數，那么某數就是這兩個數的公因數”出發，讓學生弄明白什么是公倍數，什么是公因數。然而機械記憶這樣的敘述，并不利于學生解決類似“用一張長18厘米、寬12厘米的長方形紙剪同樣大的正方形.正方形的邊長最大是多少？可以剪出幾個”的問題，少數學生分辨不清先求公倍數還是公因數。對此，每當遇到類似的問題，筆者都讓學生結合教材中的這兩幅圖形，讓他們自己感悟和確定問題求什么。由于有了這樣的應用、對比和強化的過程，這樣兩個圖形就自然成為學生解決問題的數學模型，且在頭腦中建立清晰的數學表象，從而能夠借助數學模型正確而熟練地解決問題。

三、建構數學模型的教學要點

1.注重數學模型呈現方式的豐富

片面的教學手段、單一的數學模型建構方式，不利于學生對數學問題本質的掌握和理解，所以在教學中，我們要兼用多種呈現數學模型的方式.讓學生采用不同的方式理解數學問題或概念的本質.運用不同的方法掌握數學知識。例如分數的基本性質，教材通常采用文字予以描述其數學模型的。如果照本宣科難免顯得枯燥，而且記憶單一的文字也顯得乏味，所以在總結階段.我們可以在文字表述的基礎上.增加諸如“a/b=（a×k）/（b×k）（k≠0）”的符號表述方式等.

2.關注數學模型呈現形式的選擇

數學模型的呈現方式雖然需要多樣化，但是有的也存有呈現方式的局限性。恰當的呈現方式能夠幫助學生理解問題，數學教學要關注數學模型呈現形式的選擇。例如一一間隔排列的規律有“兩端相同和兩端不同”情況.采用“兩端相同，兩端物體的個數-1=中間物體的個數，中間物體的個數+1=兩端物體的個數：兩端不同，兩端物體和中間物體個數相同”的呈現方式顯然不盡科學，因為在兩端不同的情況下不存在“中間物體”。教學時，可以借助字母和符號來進行建模，如“首尾相同：ABAB……ABA，那么A的個數-1=B的個數，B的個數+1=A的個數：首尾不同：ABAB……AB，那么A和B的個數相同”，這樣既直觀又科學。