Landau定理中上界的一個改進

郭輝，李文華

（深圳大學數學與統計學院，廣東 深圳　518060）

Landau定理中上界的一個改進

郭輝，李文華

（深圳大學數學與統計學院，廣東 深圳518060）

通過相關文獻給出的穿孔平面C{0，1}的雙曲度量的密度函數的新的下界估計，借助廣義Schwarz引理我們對Landau定理中關于上界做了進一步改進并得到了一個帶參數的上界表達式.并且當參數取到0時，此結論正好為相關文獻得到的結果.

Landau定理；全純函數；Poincar′e度量

1　引言

記?={z：|z|＜1}為單位圓，C{0，1}為穿孔平面，和ρ0，1(z)為穿孔平面雙曲度量的密度函數.眾所周知，Landau定理是復分析的一個重要的經典定理.設函數f(z)在單位圓?內全純，且不取0和1，并在原點有展式：f(z)=a0+a1z+a2z2+...，Landau定理斷言：存在一個與f無關的常數C使得

(1.1)式中常數C被稱為Landau常數.人們試圖給出其最佳值.經過多年不斷努力，最終在20世紀70年代末80年代初，先后由賴萬才[1]，Hempel[2]和Jenkins[3]彼此獨立地給出了C的精確值：

其證明方法各有不同.

盡管如此，Landau定理的顯式估計形式仍有改進的余地.1992年，李忠教授[4]在 Ahlfors[5]，Hempel[2]及 Minda[6]等人的基礎之上，給出了穿孔面 C{0，1}上雙曲度量的密度函數ρ0，1(z)的新下界，并由此得到(1.1)式的一種改進形式，其結論(見文獻［4］中定理1)如下：

定理 1.1設函數f(z)在單位圓?內全純，且不取0和1，并在原點有展式：

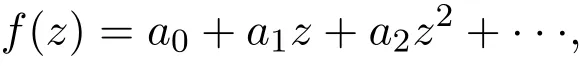
則存在一個絕對常數m＞0使得下述估計式成立：

其中C是由(1.2)式決定的常數，而

(1.3)式中的等號當且僅當f是C{0，1}的全純覆蓋映射且a0=-1時成立.

本文通過李忠教授(見文獻［4］中定理2)給出的穿孔平面C{0，1}的雙曲度量的密度函數新的下界估計，借助廣義Schwarz引理我們對定理A中關于(1.3)式做進一步改進，得到本文的主要結果如下：

定理 1.2設函數f(z)在單位圓?內全純，且不取0和1，并在原點有展式：

則存在一個絕對常數m＞0使得下述估計式成立：

其中C是由(1.2)式決定的常數，α∈(0，0.01)，且滿足

式中β是一個由α按上式確定的常數，而n為(1.4)式中定義.(1.5)式中的等號當且僅當f 是C{0，1}的全純覆蓋映射且a0=-1時成立.

注1.1當定理1.1中α=0時，(1.5)式即為(1.1)式；而且從定理1.1的證明過程可知定理1.1對定理A中的上界估計做了改進.

2　定理 1.2的證明

首先，在證明定理1.1之前，我們介紹兩個引理.

引理 2.1(廣義Schwarz引理[7-8]) 設區域D與G，其Poincar′e度量分別為

f：D→G為全純函數，則

其中等號在一點成立的充要條件是f是D到G的全純覆蓋映射.

引理 2.2[4]設ρ0，1(z)|dz|為C{0，1}的雙曲度量，其中Gauss曲率為-1.則

其中α和β與定理1.1中定義一樣.且上式中取到等號當且僅當z=-1時成立.

定理 1.1的證明首先假設|a0|=|f(0)|≤1.由引理2.1得到

我們取z=0，(2.3)式變為ρ0，1(f(0))|f′(0)|≤2，即為

將(2.4)式代入引理2.2中(2.2)式第一個不等式，得到

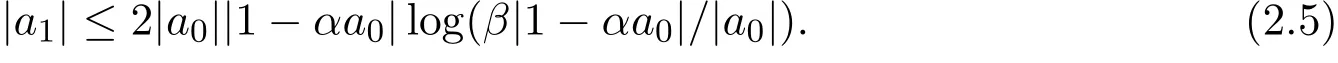
令Q(ζ)=|1-αζ|log(β|1-αζ|/|ζ|)和R(ζ)=|log|ζ||+C，并假設T(ζ)=Q(ζ)-R(ζ)，那么(2.5)式變為

比較(1.5)式，(2.5)式和(2.6)式的形式，知道要證明(1.5)式轉化為估計T(a0).根據(1.6)式，得到

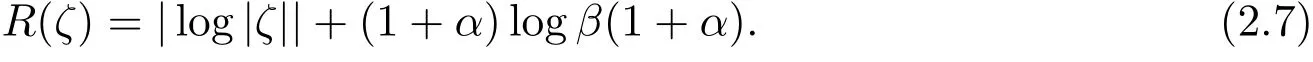
假定|ζ|≤1，那么有

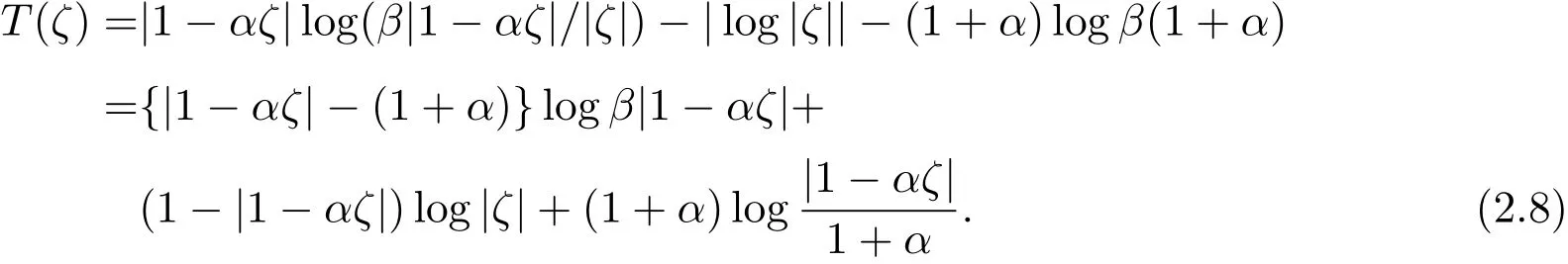
經過簡單的計算知：

又因為|ζ|≤1，利用不等式(x-1)/x≤logx，(0＜x≤1)，得到

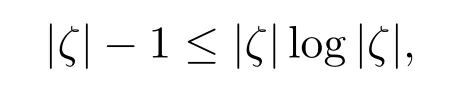
進而得到，

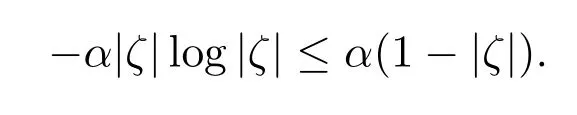
結合(2.9)式，得到：

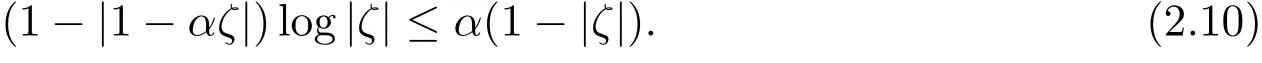
又根據(2.9)式，可知

那么由(2.8)式，(2.10)式和(2.11)式，得到

令x=Reζ，y=Imζ，對|ζ|≤1，有

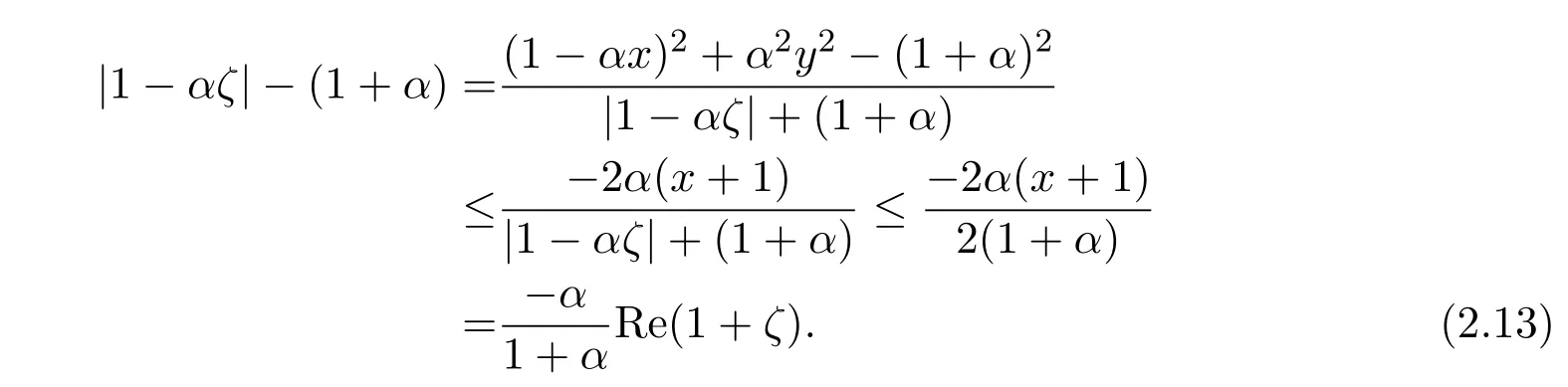
結合(2.12)式和(2.13)式，得到

因此當|a0|≤1時，令

令ζ=a0，根據(2.14)式，得到

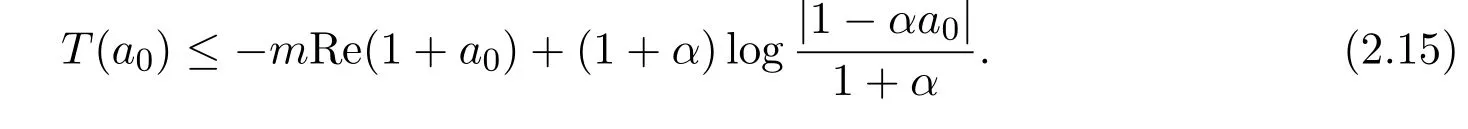
結合(2.6)式和(2.15)式，得到

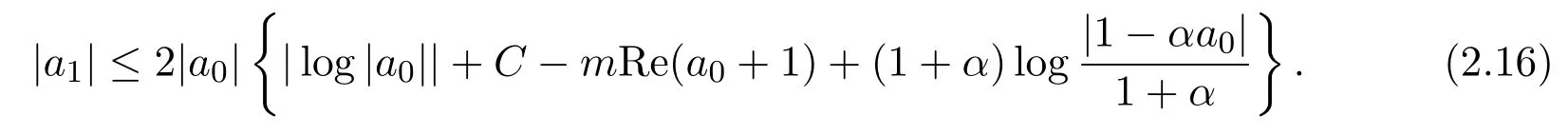
另一方面，當|a0|＞1，將上述結果應用于F=1/f，同理可以得到，

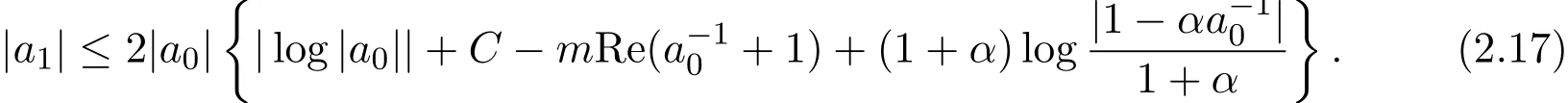
取

那么結合 (2.16)式和 (2.17)式得到 (1.5)式.由證明過程中所應用的引理 2.1及引理 2.2 知(1.5)式中的等號當且僅當f是C{0，1}的全純覆蓋映射且a0=-1時成立.

[1］Lai W C.The precise value of Hayman’s constant in Landau’s theorem[J］.Sci.in China，1978，5：495-500.

[2］Hempel J A.The Poincar′e metric on the twice punctured plane and the theorems of Landau and Schottky [J］.J.London Math.Soc.，1979，20：435-445.

[3］Jenkins J A.On explicit bounds in Landau’s theorem II[J］.Canad.J.Math.，1981，33：559-562.

[4］Li Z.A new explicit bound in Landau’s theorem[J］.Sci.in China（Series A），1992，35：463-470.

[5］Ahlfors L V.Conformal Invariants：Topics in Geometric Function Theory[M］.New York：McGraw-Hill Book Company，1973.

[6］Minda D.A reflection principle for the hyperbolic metric and applications to geometric function theory[J］. Complex Variables Theory Appl.，1987，8：129-144.

[7］李忠.復分析導引[M］.北京：北京大學出版社，2004.

[8］李忠.擬共形映射與Teichm¨uller空間[M］.北京：北京大學出版社，2013.

2010 MSC:30C20，30C35

A improvement of the upper bound in Landau theorem Guo Hui，Li Wenhua

（College of Mathematics and Statistics，Shenzhen University，Shenzhen 518060，China）

On the basis of the lower bound of the Poincar′e density of the twice-punctured plane C｛0，1｝which was given in related literature，we improve the upper bounder expression of Landau theorem and obtain a new upper bounder expression with a parameter by Schwarz Lemma.Moreover，the expression is the result in related literature when the parameter is zero.

Landau theorem，holomorphic function，Poincar′e metric

O174

A

1008-5513(2016)04-0337-05

10.3969/j.issn.1008-5513.2016.04.002

2016-04-28.

國家自然科學基金(11101290).

郭輝(1966-)，博士，教授，研究方向：復分析.