通過數學活動提升學生經驗
——以“長方形、正方形周長練習”教學為例
江蘇無錫市花園實驗小學(214000) 李梅芝
?
通過數學活動提升學生經驗
——以“長方形、正方形周長練習”教學為例
江蘇無錫市花園實驗小學(214000)李梅芝
數學活動經驗是學生在經歷數學活動的基礎上獲得的經驗,是他們經歷數學活動之后所留下的直接感受、體驗與感悟。由“長方形、正方形周長練習”這一課,談如何讓學生通過數學活動來積累、提升、內化數學活動經驗,使獲得數學經驗與理解數學知識、掌握數學技能、感悟數學思想并列,成為學生數學學習的重要目標。
數學活動數學活動經驗數學思想方法
【設計思考】
一、關注數學活動的設計
經歷數學活動是小學生積累抽象數學活動經驗的途徑。“長方形周長練習”是在學生學習了計算長方形周長的基礎上進行教學的。設計的活動要能深化學生對圖形周長意義的理解,要能使學生對“長方形和正方形周長的相關知識”有更好的理解和把握,能靈活應用周長知識解決相關的實際問題,幫助學生構建知識體系,領悟解決問題的新方法、新策略,積累解題的經驗。
二、關注個體經驗間的交流與反思
陶行知曾說:“我們要有自己的經驗做根,以這經驗所發生的知識做枝,然后別人的知識才能接得上去,別人的知識方能成為我們知識的一個有機體部分。”本課要為學生提供經驗共享的平臺,讓學生的思維在交流討論、反思總結中深入。
三、關注積極的情感體驗
經驗同時也是體驗和經歷,包括活動過程所形成的意識和信心,也包括愉悅的情感。學習過程要注重開放性、探索性,讓學生在一次次的發現中獲得一次次良好的情感體驗。
【教學過程】
一、讓學生在觀察中深化對長方形周長的體驗
師:每個同學都拿到了兩個長方形(1號:長5cm,寬4cm;2號:長7cm,寬2cm),它們的長和寬都不一樣,這兩個圖形的周長哪個更長?
師:怎樣才知道這兩個圖形的周長是多少呢?
生1:可以量出它們的長和寬,再計算。(學生測量、計算)
師(質疑):這兩個長方形的長和寬顯然是不一樣的,為什么它們的周長都是18厘米呢?
生2:因為它們一條長和一條寬的和都是9cm,乘以2就都是18cm。
生3:我覺得不能只看它的長,也不能只看它的寬,要看長與寬的和,和大的,周長才大。
生4:因為每個長方形周長都是兩個長加寬。
師(小結):看來同學們已經找到了解決問題的關鍵。是的,只要長與寬的和確定了,這個長方形的周長就確定了。
【思考:在這節課之前學生已經學會了周長計算的方法,這里出示兩個長方形,讓學生觀察它們的周長,是為了激活學生已有的關于周長知識的經驗,讓學生能夠主動、積極地進行思考。“這兩個長方形的長和寬明明都不一樣,為什么它們的周長都是18厘米呢?”沖突能夠引發學生深入探究,讓學生發現長方形的周長不能只看它的長或寬,而是看長與寬的和,從而對長方形周長計算有新的認識。】
二、有序列舉積累數學活動經驗
師:還有沒有像這樣長和寬都是整厘米數的,周長也是18厘米的長方形?
生1:只要長與寬的和是9,周長就是18cm。
生2:長是6cm,寬是3cm的長方形,長加寬的和是9cm,周長就是18cm。
……
師(追問):怎樣才能不重復也不遺漏地把這樣的長方形都找出來呢?自己先想想,再和同桌討論。
生3:我是從“長”開始想,先設定長8cm、寬1cm,再把長依次減少,寬逐漸增加,有8種情況。

生4:不對,長方形的長邊是長,他列舉的“長4cm,寬5cm”,長比寬還短。
生5:后面的4種和前面的重復了,應該列舉到長5cm,寬4cm就行了。
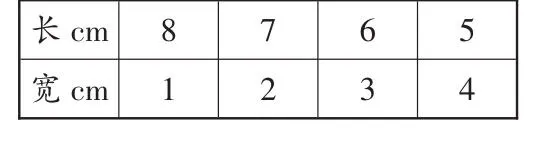
生6:我覺得寬是短邊,從寬是1cm開始考慮,列到長和寬最接近的時候更方便。
師(追問):這樣列舉有什么好處?
生7:有順序,不重復,也不遺漏。
師(小結):對!長方形周長確定了,長加寬的和就確定了。但長和寬分別是多少還不能確定,按照一定的順序有序思考,就能做到不重復不遺漏地列出所有情況。
【思考:讓學生列舉所有的長和寬都是整厘米數且周長是18的長方形,是為了讓學生知道長方形的周長后倒過去想長和寬是多少,對三年級學生來說,這樣的問題雖然開放性比較強,但學生“跳一跳”是可以解決的。該活動能讓學生體會到有序思考的數學思想方法,把低層次的活動經驗提升到了一個較高的水平。】
三、在操作活動中溝通長方形和正方形的聯系
師:正方形的周長又是由什么決定的呢?為什么?
生1:是由邊長決定的,正方形的邊長確定了,周長就確定了。
生2:長方形有長和寬兩個變化的量,而正方形四條邊都相等,所以只有邊長一個量。
師(追問):長方形和正方形有什么聯系嗎?你能從1號長方形上剪下一個盡可能大的正方形嗎?
生3:我剪的正方形的邊長是4cm。
師:有沒有不同的做法?為什么從1號長方形上剪下的正方形邊長最長只能是4cm呢?
生4:只要把長方形的長縮短到和寬一樣。寬只有4cm,所以我延著長量出4cm,剪下來的就是最大的正方形。
生5:因為寬是4cm,這個最大的正方形的邊應該是4cm,但是我用的是折的辦法(演示),把剩下的小長方形剪去,就是正方形了。
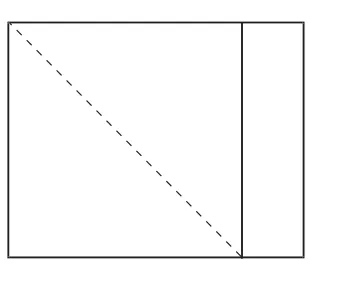
師:這兩種方法,一種是量的,另一種是折的,你認為哪種更方便?
生6:折的方便,因為沒有尺子的時候是沒辦法量的。
生7:量的話,最好兩條長邊都要量,不然剪出來的可能不標準,所以有點麻煩。
師:對!正方形是特殊的長方形,當長方形的長邊縮短到和短邊一樣長時,就是一個正方形。有時解決問題有多種角度或多種方法,學會選擇也是聰明的表現!
師:還剩下一個小長方形呢?它的周長你能求出來嗎?試試看。
生8:也可以量出它的長和寬,再計算。
師(追問):不用尺也能算出它的周長嗎?
生9:根本不需要量,因為從圖上就能發現,這個小長方形的長是4cm,寬是5-4=1cm,直接計算就行了。
師:對,仔細觀察圖形,就能推算出它的長和寬,這是一個好辦法。
【思考:有了關于計算長方形周長的活動經驗,學生會自覺地運用這一經驗來解決正方形周長的問題。這里,教師聯系圖形的特征溝通了長方形和正方形的關系,在溝通中學生能夠不局限于一種策略求得圖形的周長,初步感受到觀察和猜想也是好方法,強化了學生行為操作和思維操作中獲得的經驗。】
四、體會“畫草圖”也是解決問題的策略
1.用畫草圖的方法研究2號長方形
師:如果也想從2號長方形上剪下一個最大的正方形,邊長應該是幾?這次不剪,老師把2號長方形畫在黑板上,你能不能在圖上表示出這個最大的正方形呢?(生到黑板上操作)看著這幅圖你能求出剩下的長方形的周長嗎?
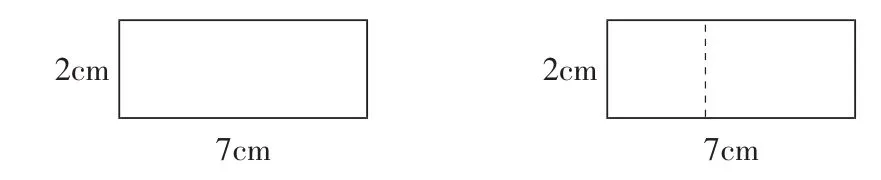
生1:(5+2)×2=14cm。
師:很好,還有沒有更巧妙的方法來求這個小長方形的周長呢?請認真觀察,這里長加寬的和與原長方形的長有什么關系?
生2:這個小長方形一條長加一條寬正好是原來長方形的長——7cm,所以周長是7×2=14cm。
師(追問):我們在研究2號長方形時沒有剪而是用了什么方法?
生3:我們畫了一個圖。
師(追問):你覺得畫圖有什么好處?
生4:畫圖很方便。
生5:圖上標好數據,很容易找到思路。
師(小結):遇到問題,可以試著畫畫圖,有可能會有意外收獲哦!
2.應用畫圖策略解決問題
師:用兩個長都是6分米,寬都是3分米的長方形,拼成一個長方形或正方形,請計算拼成圖形的周長。
師:能把腦子里拼成的圖形畫下來嗎?試著先畫圖,再列式計算。拼出的圖形周長和原來兩個小長方形的周長總和相比,你又發現了什么?
生1:拼成長方形,周長比原來少了2條寬,拼成正方形,周長比原來少了2條長。
師:請具體說明。
生1:原來一個長方形的周長是(6+3)×2=18,兩個就是18×2=36。拼出的長方形周長是(6+6+3)×2=30,36-30=6,就是2個寬。
生2:可以不用算,看圖就知道重疊的兩條寬藏在里面了,計算時可以少算這兩條寬。
師:你很會觀察,通過看圖發現規律。這里只有兩個圖形的拼接,如果更多的圖形拼在一起呢?
(生討論交流)
【思考:對于三年級的學生來說,要精確地畫圖是比較費時和費力的,而解決問題往往只需要一張簡單的示意圖,因此教師有意識地讓學生嘗試畫圖,偏重于讓學生體驗策略、積累經驗。“能把腦子里拼成的圖形畫下來嗎?”這里讓學生先想再畫,避免盲目地畫,而是帶著思考畫。“可以不用算,看圖就知道重疊的兩條寬藏在里面了,計算周長就可以少算這兩條寬。”從學生的回答能知道,學生已經不局限于用筆算一算,而知道通過看圖來尋找思路了。“你很會觀察,通過看圖發現規律。這里只有兩個圖形的拼接,如果更多的圖形拼在一起呢?”這里的討論交流,是經驗的分享,是思維的碰撞,為學生活動經驗的拓展提供了空間。】
五、解決問題(獨立解答,小組分享,反思收獲)
1.走迷宮游戲
規則:以五角星為起點,繞著迷宮走一圈,先走完一周回到起點者勝。(圖略)
2.一個正方形操場邊長為40米,小明繞操場跑了3圈,他一共跑了多少米?
3.一個長方形的寬是20分米,長是寬的2倍,長方形的周長是多少分米?
4.小明的爸爸計劃靠著院墻用籬笆圍建一個養雞場,養雞場長12米,寬8米,需要籬笆多少米?
【思考:學生獨立解決實際問題的過程是“經驗”應用的過程,把“死”的知識“活”化的過程。學生在應用中會遇到各種問題,有的學生能找到解題策略,有的學生會“卡”在某個環節,有的甚至會對原來獲得的經驗產生懷疑。通過交流與反思,學生可以修正原來錯誤的經驗,強化并豐富已有的經驗,學會從數學的角度觀察事物、思考問題,產生對數學的興趣以及學好數學的愿望。】
史寧中先生認為:“基本活動經驗是指學生親自或間接經歷了活動過程而獲得的經驗。”對于練習課來說,要改變枯燥的練習課,教師就要嘗試把知識進行整合,設計以學生原有經驗為起點的充分體現數學本質的活動,讓學生經歷觀察、操作、實驗、猜想、驗證等活動過程,積累解決問題的策略經驗,感悟數學思想方法。在此過程中,要注重引導學生交流與反思,及時幫助學生提升和內化數學活動經驗,幫助他們形成比較完整的數學認知結構,真正把數學課程標準提出的“將學生獲得數學活動經驗作為數學教學目標”的要求落到實處。
(責編金鈴)
G623.5
A
1007-9068(2016)20-007

