如何引導學生積累基本的數學活動經驗
——以“平行四邊形面積”一課教學為例

浙江新昌縣教體局教研室（312500）　章秀惠

?

如何引導學生積累基本的數學活動經驗
——以“平行四邊形面積”一課教學為例

浙江新昌縣教體局教研室（312500）章秀惠

數學活動經驗的積累與發(fā)展，離不開教師有意識的點撥和訓練，更離不開學生自覺的領悟和應用。因此，教師要精心設計、組織好每一個數學活動，讓學生親身經歷由探究到鞏固深化再到應用的過程，使他們獲得個性化的感受和體驗，積累廣泛的、豐富的數學活動經驗。

數學活動經驗生成積累應用內化平行四邊形面積

教育家杜威認為：“一盎司經驗勝過一噸理論。”因此，在數學教學中，教師引導和幫助學生積累基本的數學活動經驗十分必要。下面，我以“平行四邊形面積”的教學為例，希望能給一線教師以啟示。

一、直面學生錯誤，尊重把握活動經驗

師：比一比，哪個圖形的面積大？

生1：正方形的面積大。

生2：平行四邊形的面積大。

師：到底誰的面積大？怎么算？（生先獨立測量所需數據，計算兩個圖形的面積，再匯報交流）

生3：長方形的長是6厘米，寬是4厘米，所以面積是24平方厘米。

生4：平行四邊形的長是7厘米，寬是5厘米，所以面積是35平方厘米。

師：認為平行四邊形面積是35平方厘米的同學請舉手。（大部分學生舉手）為什么？

生5：因為長方形的面積是這么算的，那么平行四邊形的面積也可以這么算。

……

思考：

學生原有的數學活動經驗，必然會影響他們參與新的數學活動的經歷、感受和體驗，從而影響學生新經驗的積累。如上述教學中，通過量一量、算一算的活動，暴露了學生用“底×鄰邊”求平行四邊形面積的思維過程，而且基于計算長方形面積的經驗遷移，學生堅信平行四邊形面積=底×鄰邊。雖然學生已有的認知可能是錯誤的，但教師把握了學生數學活動經驗的起始狀態(tài)，確定了學生的能力起點，為學生學習新知打下了良好的基礎。

二、引導學生探究，生成積累活動經驗

1.推導公式，經歷方格度量的過程，積累和提升策略性、方法性經驗

師：到底誰對？一起來研究。平行四邊形有什么特征？

生：易變。

（師拿出長7厘米、寬5厘米的可拉動的平行四邊形框，并將平行四邊形框拉成了長方形框，如下圖）

師：這個長方形的長與平行四邊形的底有什么聯系？鄰邊呢？

生1：平行四邊形被拉成長方形后，長是7厘米，寬還是5厘米，所以平行四邊形面積是35平方厘米。

師：有不同意見嗎？

生2：因為平行四邊形的底是7厘米，高是3厘米，所以它的面積是21平方厘米。

師：你量了什么？

生2：高。

師：7×5=35（平方厘米），7×3=21（平方厘米），怎么比較大小？

生3：因為平行四邊形被拉成長方形，所以面積比平行四邊形大。（課件把平行四邊形移入格子圖里進行驗證，生數格子）

生4：完整的有15小格，不完整的小格拼一下，一共有21格。（師根據生的回答，演示割補法，如下圖）

生5：底乘高，所以平行四邊形的面積是21平方厘米。

師：底乘高，這樣算是什么道理？同桌商量。（生討論略）

師：把平行四邊形沿高裁下來，拼成長方形（如下圖），你發(fā)現了什么？

生6：平行四邊形的底變成了長方形的長，高變成了長方形的寬，所以它們的面積是一樣的。

師：那么，平行四邊形的面積可以怎么算？

生7：平行四邊形面積=底×高。

師：剛才是將平行四邊形沿高裁一刀拼成長方形，你覺得還可以從哪里裁一刀將平行四邊形拼成長方形？大家試一試。

生8：

生9：只要沿底邊上的高裁都可以。

師：為什么要沿著高裁？

生10：不沿著高裁，就拼不出長方形。

生11：長方形的角是直角，沿著高裁才能拼出長方形。

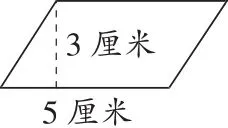
師（出示右圖）：能算出它的面積嗎？

生12：5×3=15（平方厘米）。

師：在方格子圖里驗證一下。（生驗證略）

師（出示“平行四邊形面積=底×高”）：如果用S表示平行四邊形的面積，用a表示平行四邊形的底，用h表示平行四邊形的高，那平行四邊形面積的字母表示公式是什么？

生13：S=a×h或S=a·h。

生14：S=ah。

2.充分說理（展示糾正錯誤的理由）

師：回頭看看，平行四邊形面積等于35平方厘米為什么錯了？（出示下圖）看圖并說一說理由。

生15：平行四邊形的高不等于鄰邊，用底乘鄰邊算不對。

生16：空白部分是多出來的部分。

師：平行四邊形面積能用底乘鄰邊算嗎？

生：不能。

……

思考：

教師十分重視數學活動的設計與組織，引導學生在自主探究、合作交流中經歷平行四邊形面積公式的推導過程，使學生在觀察、猜想、驗證、推理、歸納中積累數學活動經驗，形成轉化的數學思想方法。尤其是教師的兩次追問“你覺得還可以從哪里裁一刀將平行四邊形拼成長方形”“為什么要沿著高裁”，引導學生在活動中充分體驗、感悟，積累獨特的個性經驗（不同的剪法）。而且，教師讓學生在思維碰撞中逐漸形成統一的認識——平行四邊形轉化成長方形的關鍵是利用對邊相等，創(chuàng)造出四個直角，從而使學生積累了富有個性色彩的數學活動經驗。

三、巧設變式練習，鞏固應用活動經驗

（1）計算下面各圖的面積。（單位：厘米）

（生先獨立練習，再匯報交流）

生1：第一個圖形的面積為10×15=150（平方厘米）。

師：你將它看成怎樣的長方形？

生1：將它看成長是15厘米，寬是10厘米的長方形。

生2：第二個圖形的面積為12×6=72（平方厘米）。

師：有同學將它看成是8×6的長方形嗎？

生：沒有。

師：有沒有辦法用底8厘米乘高？

生3：72÷8=9（厘米）就是高。

（2）比較下列平行四邊形的面積。（單位：厘米）

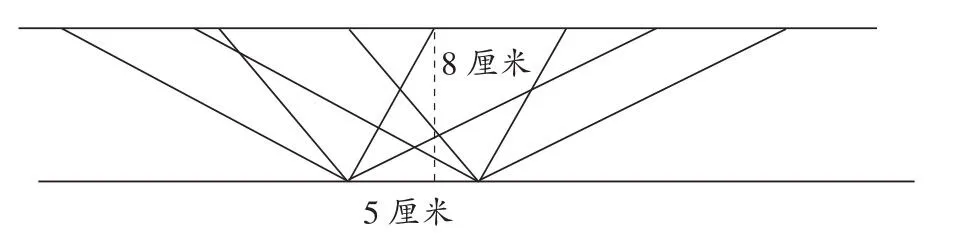
師：這些平行四邊形的面積相等嗎？（生意見不統一）請同學們算出這些平行四邊形的面積。（生計算）

生：它們的面積都一樣。

師：現在改變看法了嗎？每個平行四邊形的底是多少，高是多少，面積是多少？

師生歸納得出：等底等高的平行四邊形面積一定相等。

……

思考：

學生數學活動經驗的積累是一個循序漸進，層層遞進的過程。習題（1）使學生對平行四邊形底和高的對應關系有深入的理解；習題（2）將多個面積相等且形狀各異的平行四邊形呈現在學生面前，讓學生觀察和計算，引導他們產生新的發(fā)現——等底等高的平行四邊形面積一定相等。這樣教學，使學生的視野更開闊，對等積變形的思想也有了更深入的理解。這里，教師對習題（1）、習題（2）的設計和開發(fā)層層遞進，注重引導學生對新經驗的運用，提高了學生解決問題的能力。

四、親歷反思過程，升華內化活動經驗

師：今天學習了什么知識？

生1：學習如何求平行四邊形的面積。

生2：我懂得了等底等高的平行四邊形面積相等。

……

師：我們是如何學會的？今天我們把平行四邊形轉化成長方形，求出了面積，這樣的方法叫轉化。

……

思考：

荷蘭數學家弗賴登塔爾指出：“反思是數學思維活動的核心和動力。”在課堂總結延伸環(huán)節(jié)，教師通過問題“今天學習了什么知識”“我們是如何學會的”，引導學生反省自己的思維過程，促使學生形成新的經驗，并自覺地運用于后續(xù)學習之中。這樣的反思，可以深化對問題的理解，優(yōu)化思維過程，溝通知識間的內在聯系，使學生個體獲取的數學實踐經驗上升為思維經驗，為可持續(xù)發(fā)展服務。

“紙上得來終覺淺，絕知此事要躬行。”經驗是在活動中積累的，學生只有親自參與數學活動，才能在獨立思考中不斷積累直接的數學活動經驗，即“數學活動經驗需要在做的過程中和思考的過程中積淀”。因此，教師要精心設計、組織好每一個數學活動，讓學生親身經歷由探究到鞏固深化再到應用的過程，使他們獲得個性化的感受和體驗，積累廣泛的、豐富的數學活動經驗。

（責編杜華）

G623.5

A

1007-9068（2016）20-026